이번에 리뷰할 논문은 오랜만에 optical flow 논문입니다. 해당 논문을 읽게 된 이유는 제가 요새 관심 있어 하는 homography estimation 분야는 image registration을 수행할 수 있으며 마찬가지로 optical flow도 image registration을 수행할 수 있기에 혹시나 유용한 내용이 있을까 싶어 찾아보게되었습니다.
Intro
기존의 딥러닝 기반 optical flow 방법론들은 cost volume을 활용하는 것이 매우 지배적이라고 합니다. 하지만 이러한 cost volume 방식은 local correlation만을 잘 볼 수 있다는 한계점으로 인해 large displacement, 즉 두 영상 사이의 큰 격차가 있을 경우에는 잘 동작하지 못한다는 단점이 존재합니다.
이는 사전의 정의된 크기가 필요로만 하는 cost volume이 볼륨의 채널 축을 search space로 놓고 convolution 연산을 통해 flow를 regression하기 때문인데, 이러한 cost volume의 요구 사항은 local range에 대하여 search space를 제한하기 때문에 앞에서도 말씀드린 large displacement에 취약하게 됩니다.
이러한 문제를 해결하기 위해서 최근의 SOTA 방법론들은 매번 다른 iteration stage마다 서로 다른 local cost volume에 대하여 컨볼루션을 연산하는 등 iterative한 방식을 통해 search space를 local에서 global로 점차 확장해나가는 방식을 적용했다고 합니다. 이러한 방법들은 좋은 성능을 보여주게 되었지만 아쉽게도 iterative stage가 많을수록 inferencfe time 역시 linear하게 증가했다고 합니다.
그래서 저자는 매우 정확하면서도 (기존의 iterative refinement 없이) 효율적이게 접근할 수 있는 방법이 없을까 라는 고민과 함께 optical flow가 아닌 또 다른 visual correspondence problem에 관심을 가집니다. 그 중에서 가장 대표적으로 SuperGlue와 LoFTR을 언급하는데, 해당 방법론들은 Transformer를 활용함으로써 feature descriptor 사이에 상호 관계를 잘 규정하고, matcinh layer를 통하여 명확하게 대응관계를 출력한다고 합니다.
이러한 sparse matching 분야에 영감을 받아 저자는 사전의 정의된 local cost volume에 추가적인 컨볼루션 연산을 수행하는 것 대신, optical flow를 global matching problem으로 재정의하여 문제를 해결하였다고 합니다.
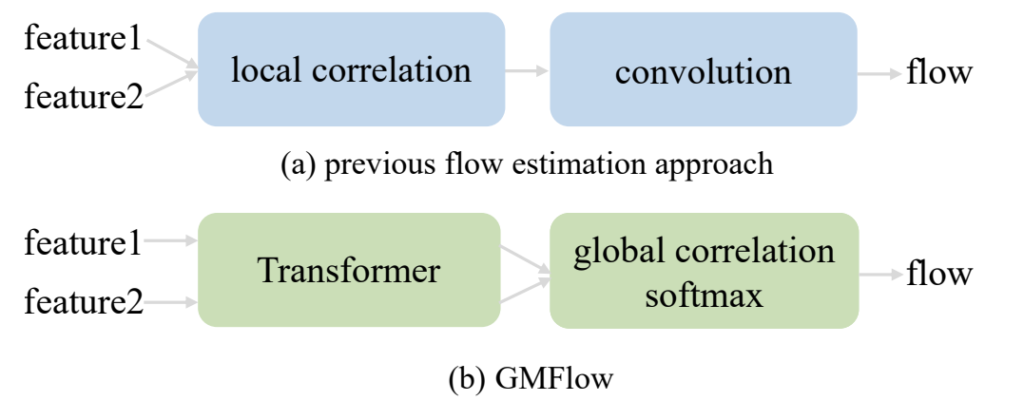
즉 기존의 방법론들은 어떻게 하면 두 영상 사이의 (local) correlation을 잘 살피고 이에 대하여 cost volume을 정의한다음 이를 컨볼루션 연산을 통해 최종적인 flow를 계산하였다면, 저자는 기존의 sparse matching 분야들처럼 transformer를 통하여 두 영상간의 관계성을 명확히 표현하고, global correlation을 계산하는 softmax layer를 통해 global matching problem으로 optical flow를 재정의하였다고 합니다
이렇게만 보면 그냥 sparse matching 분야에서 제안된 방법론들을 optical flow에 그냥 적용해본 것 아닌가? 라는 생각이 드는 것에 대하여 저자도 의식하였는지, 저자도 최대한 자신들의 contribution에 대하여 추가적인 설명을 수행하는데 먼저 optical flow는 모든 픽셀들에 대하여 대응점을 계산해야 하는 문제이며 현재의 방법론들은 대부분 local cost volume을 어떻게 잘 활용해야 성능이 좋을지에 대해서만 연구를 수행하고 있다는 것에 한계를 지적합니다. 그러면서 자신들이 이러한 기존의 틀을 깨고 optical flow 역시 global matching problem으로 풀 수 있다는 것을 보여주었다는 점에서 의미가 있다는 식으로 주장을 합니다.
아무튼 다시 본론으로 들어와서, 저자가 해당 논문에서 제안하는 것은 (1)Transformer를 활용하여 self, cross-attention을 통해 두 영상 사이의 보다 명확한 dense feature를 추출한다는 점, (2) 이렇게 추출된 correlating feature들로부터 feature similiarty를 계산한 다음 softmax matcinh layer로 최종 flow를 예측한다는 점으로 볼 수 있겠습니다.
Method
보다 자세한 설명에 들어가기 앞서, 먼저 필요한 개념에 대한 formulation을 시작하고 넘어가겠습니다.
주어진 두 frame 이미지를 I_{1}, I_{2} 라고 하며 해당 프레임들을 weight sharing CNN에 입력으로 제공하여 추출한 dense feature를 F_{1}, F_{2} 라고 합니다. 이때Dense Feature의 shape은 (H x W x D) 입니다.
그 후 두 프레임의 correspondence가 얼마나 유사한지에 대하여 측정하기 위해, 저자는 각 픽셀레벨에 대한 feature similarity를 아래와 같이 계산하였다고 합니다.
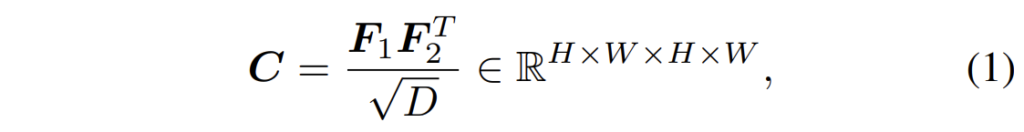
여기서 C는 correlation matrix로 표현되며 F1과 F2 사이의 픽셀별 correlation을 표현한다고 이해하시면 될 것 같습니다. correspondence한 부분을 명확하게 추출하기 위해서 가장 흔한 방법으로는 그저 high correlation 값을 내포하는 지점을 선택할 수도 있겠으나, 이러한 방법은 미분이 불가능하다고 합니다.
그래서 저자는 미분 가능한 matcinh layer를 활용하였는데 보다 자세히 설명드리자면 C의 마지막 2개의 차원들ㅇ ㅔ대하여 먼저 softmax로 normalize를 수행하여 matching distribtuion을 생성합니다.
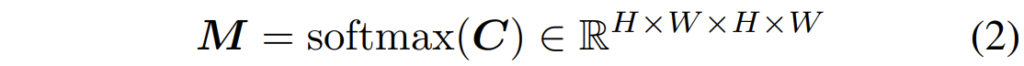
그 다음, 2D 영상 좌표를 표현하는 pixel grid G에 대하여 matching distribution M을 곱해줌으로써 correspondence \hat{G}를 계산합니다.
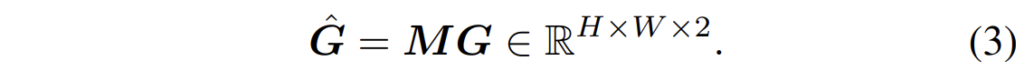
최종적으로 optical flow V는 두 corresponding pixel corrdinate의 차이를 계산함으로써 만들 수 있습니다.
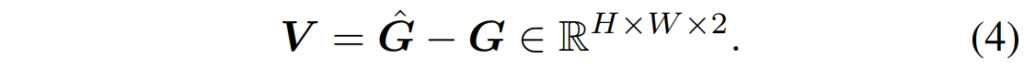
이러한 softmax 기반의 방법론은 end-to-end traning을 할 수 있을 뿐만 아니라, sub-pixel의 정확도에도 좋은 영향을 준다고 저자는 주장하고 있습니다.
Feature Enhancement
자 그러면 본격적으로 저자가 제안하는 Transformer 방법에 대해서 설명하도록 하겠습니다. 일단 위에서 설명한 F_{1}, F_{2} 를 Transformer block의 입력으로 활용을 하게 됩니다.
이 때 두 feature에는 어떠한 spatial position에 대한 정보가 없기 때문에 저자는 DETR과 동일하게 고정된 2d sin, cos positional encoding을 더해주었다고 합니다. 이렇게 position information을 더해주게 된다면 matching process에서 feature의 유사도 뿐만 아니라 spatial distance까지 보다 정확하게 계산을 할 수 있어 성능에 좋은 영향을 끼친다고 합니다. (근데 요새 transformer backbone들은 positional encoding을 convolution 연산으로 대체하는 편이라.. 해당 논문은 그런쪽 실험은 진행하지 않은 듯 합니다.)
아무튼 position information을 더해준 다음에는, 이제 6개의 self & cross attention과 feed-forward network로 구성된 transformer block을 통과하게 됩니다.
이때 self-attention 연산은 저희가 잘 알고 있는 query, key, value를 통한 attention 연산을 수행하는 것이며 cross attention의 경우 key와 value는 고정이지만 query로 사용되는 feature를 다르게 제공함으로써 mutual dependency를 제공받게 됩니다.
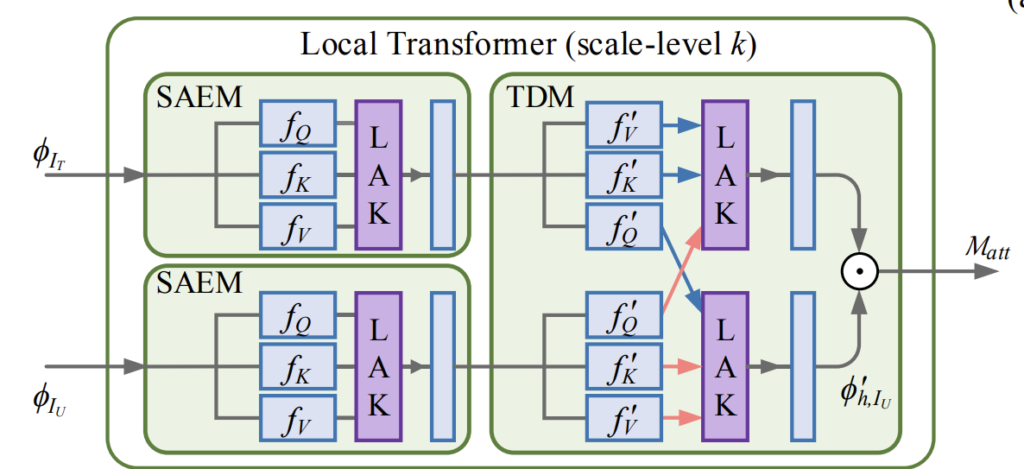
그림 2는 위의 내용에 대하여 이해를 돕고자 첨부한 그림으로 사실 논문에서 제안하는 방법론의 그림은 아니며 다른 방법론의 그림을 제가 그저 self & corss-attention에 대한 이해를 도와드리고자 첨부해보았습니다.
아무튼 수식적으로 표현하면 다음과 같이 나타낼 수 있겠습니다.
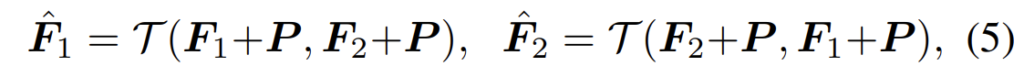
여기서 T는 Transformer를, P는 positional encoding을 의미합니다.
한가지 더 설명하고 넘어갈 점은 아무래도 standard Transformer 구조를 그대로 활용하면 입력 feature의 해상도에 따라 quadratic한 연산 복잡성을 지니게 되는데 optical flow의 경우 영상의 해상도가 크다 보니 연산량이 크게 늘어난다는 단점이 존재로 합니다.
저자도 이를 의색하여 Swin Transformer를 베이스로 활용한 후, 이때 고정된 윈도우 사이즈를 가지는 Swin과 달리, local window의 수를 고정시켜 윈도우 사이즈를 feature size에 맞게 설정하였다고 합니다.
즉 저자는 input feature의 size가 기존 H x W였다면 이를 K x K 개의 윈도우로 구분지었으며(즉 각각의 사이즈는 H/K x W/K를 의미합니다.) 이들에 대하여 각각의 local window에 대해 독립적으로 self and corss attention을 계산하였다고 합니다.
매 2번의 consecutive local window 이후에는, window partition을 H/2K, W/2K로 SIFT를 하여 cross window connection를 수행하였다고 합니다. 음.. 일단 논문에서 그림도 하나 없이 글로만 간략하게 서술하다보니 저도 제대로 이해를 하지 못한 채로 해당 부분을 작성한 것 같네요. 양해 부탁합니다.
Flow Propagation
앞부분에서 설명드린 Softmax-based flow estimation 방법론은 두 대응되는 이미지들 사이에 corresponding pixel들이 모두 보인다는 조건이 존재로만 합니다. 하지만 이러한 가정들은 occlusion과 경계면 근처의 픽셀들인 경우 깨져버리기 때문에 저자는 이를 보완하고자 optical flow와 영상 그 자체의 높은 구조적 유사도를 공유하도록 하는 feature self-similarity를 추정함으로써 매칭된 픽셀과 그렇지 못한 픽셀들을 구분하도록 하였다고 합니다.
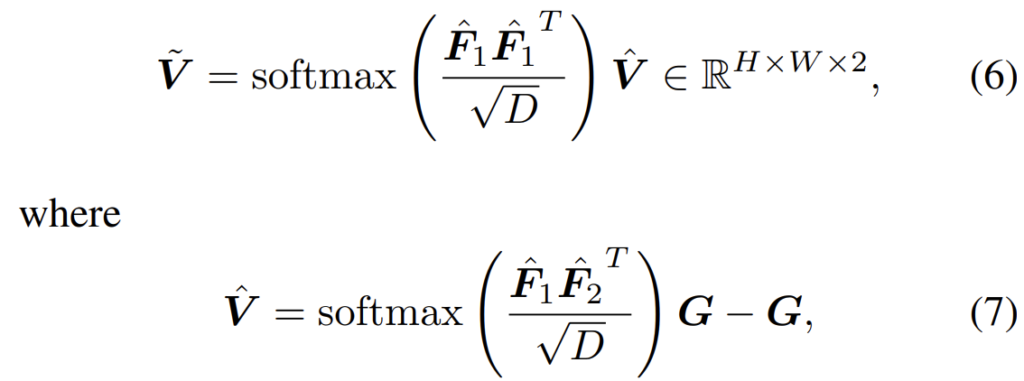
이러한 연산은 위 수식과 같은 방식으로 진행이 된다고 합니다.
여기서 \hat{V}는 위에서도 언급한 flow map이라고 한다면 해당 flow map에 다시 한번 동일 feature의 similarity를 계산하여 곱해줌으로써 해결할 수 있다고 하는데 음.. 이것도 왜 그런건지는 잘 모르겠네요..?
학습 loss는 supervised optical flow 방법론이어서 GT와 비교하는 형식으로 적용됩니다.
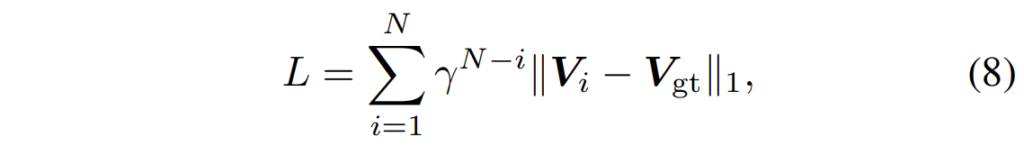
Experiments
모델 학습은 기존의 방법론들과 동일하게 FlyingChairs라는 합성 데이터 셋으로 학습한 후 Sinte과 KIIT의 학습 데이터로 평가를 진행하였다고 합니다.
평가 방법은 end-point-error(EPE) loss로 예측한 값과 실제 정답값 사이의 L2 norm을 계산하여 평균을 내는 방식입니다.
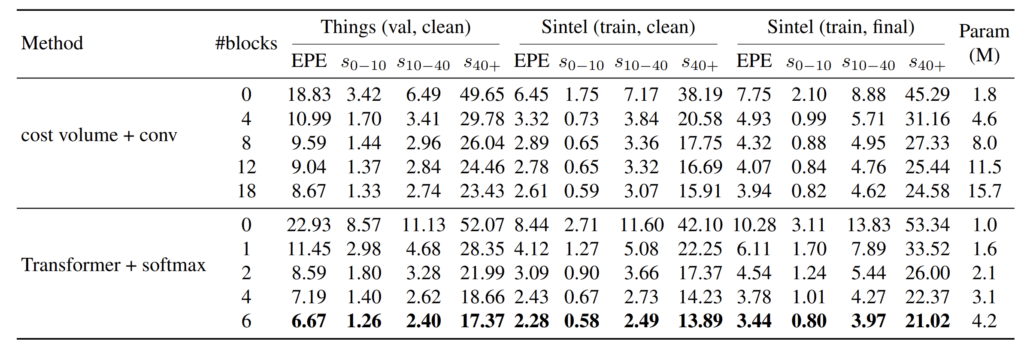
결과를 살펴보시면 기존의 cost volume과 컨볼루션의 조합과 비교하였을 때 저자가 새로 제안하는 Transformer & softmax 조합이 더 적은 양의 블록과 파라미터 개수로도 더 우수한 성능 성능을 보여주고 있습니다.
이는 large displacement에 대해서 더 잘 해결하였기에 유의미한 성능 향상이 있는 것으로 판단되는데 저기 s_{n}-{m} 의 의미는 ground truth의 flow magnitude 값이 n~m 사이일 때의 EPE 성능을 보인 것이라고 이해하시면 됩니다.
즉 Depth estimation에서 거리 별로 성능을 보이는 것처럼, 여기도 GT flow의 magnitude 값에 따라서 평가 성능을 보였다고 이해하시면 되는데 Things 데이터 셋 기준 0~10지점, 10~40 지점에서는 cost volume & CNN과 Transforemr & softmax 결과의 차이가 각각 0.07, 0.34인 반면 40이상인 지점에서의 EPE 결과를 보시면 5.94로 상당히 큰 차이가 나는 것을 확인할 수 있습니다.
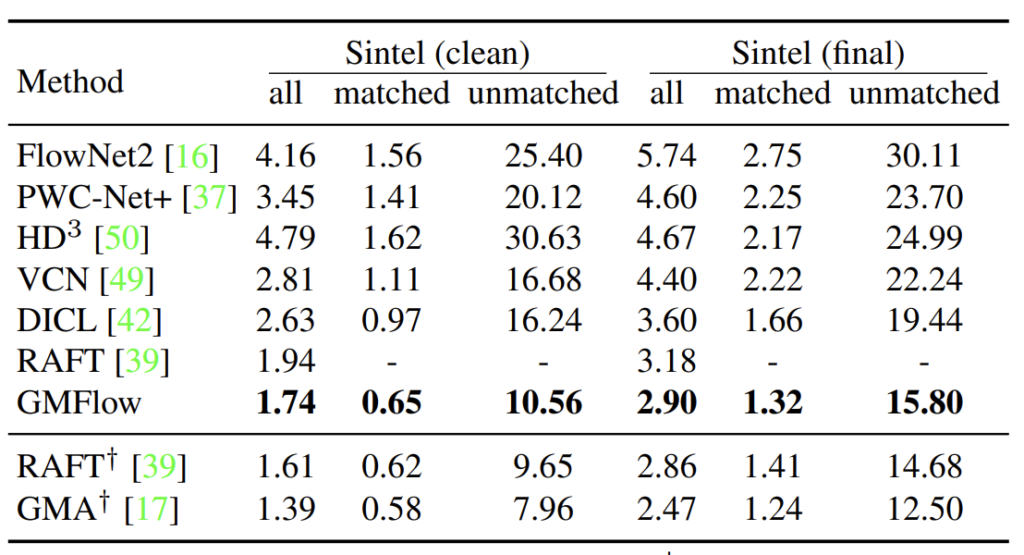
위의 테이블은 다른 방법론들과의 SIntel 정량적 비교 결과입니다. 보시면 GMFlow가 가장 좋은 성능을 보여주고 있으며 밑에 RAFT와 GMA의 경우에는 저 십자가 표시가 iterative refinement한 결과로 이해하시면 됩니다. 즉 십자가가 없는 모델들은 두 영상에 대해서만 결과를 낸 것이며 맨 밑과 밑에서 두번째의 RAFT와 GMA는 flow 결과롤 반복적으로 refine한 것으로 성능은 더 좋게 나올 수 있으나 속도가 느리다는 단점을 가지고 있습니다.
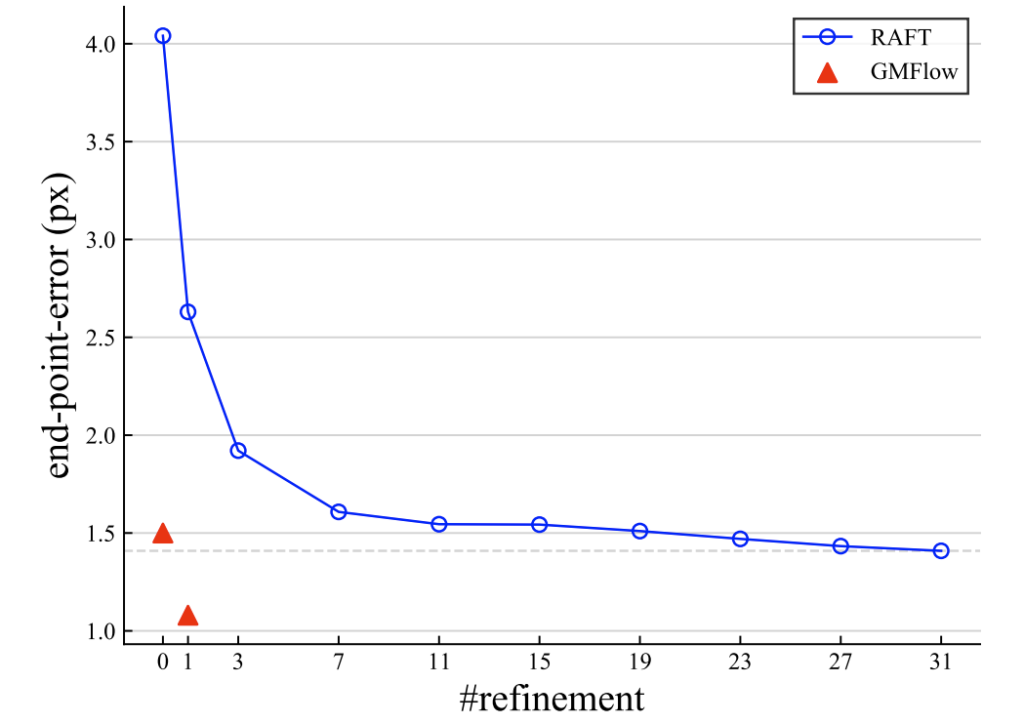
실제로 GMFlow 역시 refinement를 한번 더 할 수 있다고 하는데 refinement가 30회가 넘는 RAFT과 비교하여 한번만 refinement 하더라도 EPE 에러 값이 훨씬 낮은 것을 볼 수 있으며 실제 속도 역시 66ms vs 91 ms로 더 빠른 것을 확인할 수 있습니다.
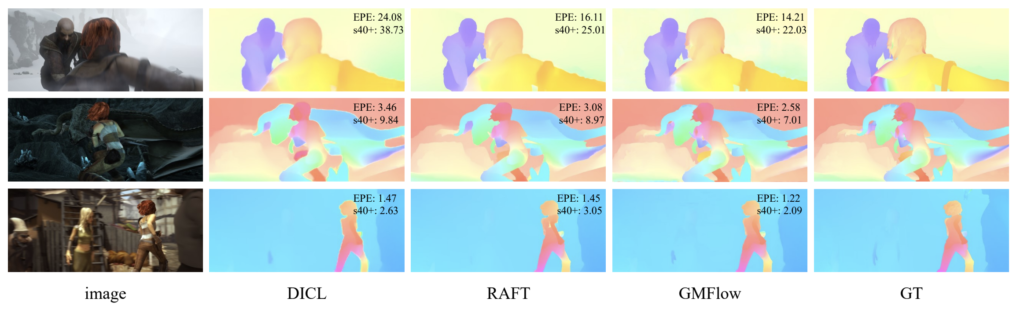
다음은 정성적 결과입니다. 보시면 논문에서 제안하는 방법론이 SOTA 방법론들과 비교해서 s40+의 결과도 더 좋은 것을 볼 수 있습니다.