제가 이번에 리뷰할 논문은 VIO에 관련된 논문입니다. VIO 논문은 처음 읽어봐서 잘 모르는 부분도 많았습니다. 그리고 이번에 리뷰할 논문은 수식적으로 모델링을 한 부분이 있어서, 수식이 많네요. 낯선 내용이 많기 때문에 수학적으로 모델링 하는 부분들도 모두 포함했습니다..
Abstract
multi-spectral 데이터는 VO에서 많은 정보를 줄 수 있지만, 모달리티간의 차이가 있기 때문에 잘 사용하지 않았다. 이 논문에서는 multi-spectral 데이터를 활용하기 위한 방안을 제시하였다. (1)각 모달리티에서 feature을 tracking하고, (2)windowed bundle adjustment로 motion을 추정한 다음, (3)스테레오 환경의 기하학적 정보를 활용하여missing scale을 회복한다.
추정의 강인성을 얻기 위해 feature 시차 기반의 적절한 keyframe을 선택하고, stereo 쌍의 상호 정보 보완을 최대화한다. 게다가, 이미지 품질이 떨어지는 문제상황을 해결하기 위해 error-state Kalman 필터 프레임워크로 통합된다.
절대 및 상대 포즈를 제시하고 visual 정보가 없을 경우 IMU정보에 의존하는 복구 알고리즘을 제시하여 상대 포즈의 우수성을 보인다.
Introduction
VO는 GNSS(범지구위성항법 시스템)보다 오차 정도가 작고, GPS 신호가 방해를 받거나 indoor 환경이라 신호가 잡히지 않을 경우에 활용할 수 있다는 장점이 있어 활발히 연구되고 있다.
그러나 이러한 VO는 상대적 변환이 추정되기 때문에 시간이 지날수로 오차가 누적되어 상당한 오류가 생길 수 있다는 문제가 있다. image 기반의 localisation은 inertial기반의 localisation에 비해 덜 심하다. 이러한 문제를 해결하기 위해 VO와 inertial기반의 데이터는 강인한 localisation을 위해 다른 센서와 합쳐진다.
또한, visible 데이터를 주로 활용한다. multispectal은 의학분야에서 많이 활용되었으며, localisation에서는 거의 처음이다. 이는 다른 이미지보다 더 선명하기 때문이다.
이 논문의 contribution은 다음과 같다.
- stereo image 매칭. pose와 scale 추정 과정을 분리하고 scale 추정에서 multispectral을 활용한다. 이때, robust 한 추정을 위해 한번 모든 feature 고려
- 각 카메라는 독립적으로 사용됨
- 성능 능가
- multispectral VO에 inertial 데이터를 활용하여 새로운 localisation 해결책 제시.
Global Multispectral Visual Odometry(GMS-VO)
A. Feature Detection and Tracking
optical flow기반의 방식을 이용한다.
GFTT(Good Feature To Track) 알고리즘을 이용하여 feature 탐지 후 pyramid Lucas-Kanade로 연속적인 이미지의 특징점 위치를 찾는다. 이때 정확한 삼각측량을 위해서 t와 t+1 사이에 충분한 변환이 있어야 하고, 따라서 [VINS-Mono: A robust and versatile monocular visual-inertial state estimator, IEEE Trans. Robot. (2018)]의 ****keyframe을 찾는 방식을 이용한다. 이때 매 iteration마다 essential matrix를 추정할 때, epipolar 제약 조건을 보장하기 위해 outlier를 탐지하고 제거하며, 이는 5개의 점을 이용한 RANSAC방식을 이용한다.
B. 3D Reconstruction
essential matrix로부터 SVD를 통해 상대적 변환 관계를 얻는다. 각 모달리티는 독립적으로 추정하고, point cloud를 생성한다. 두 모달리티가 서로 다른 좌표계이지만 동일하게 움직이므로 공동좌표계로 모든 점을 표현하여 공통된 단일 point-cloud를 생성한다.
두 pose 추정치의 평균 회전 및 변환을 근사치로 선택한다.
변환 관계를 이용하여 단순하게 변환할 수 있으므로, 왼쪽 카메라 좌표를 시스템의 원점으로 하고, 오른쪽 카메라의 점과 좌표를 왼쪽 기준으로 옮긴다.이후 모두 함께 bundle adjustment framework를 통해 refine한다.
C. Scale Recovery
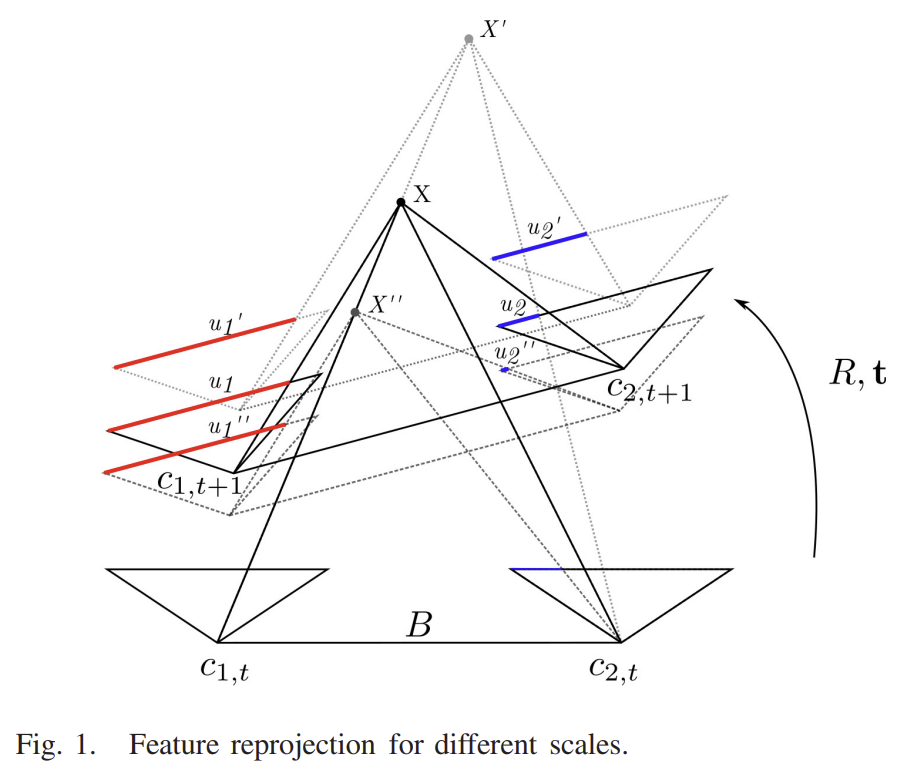
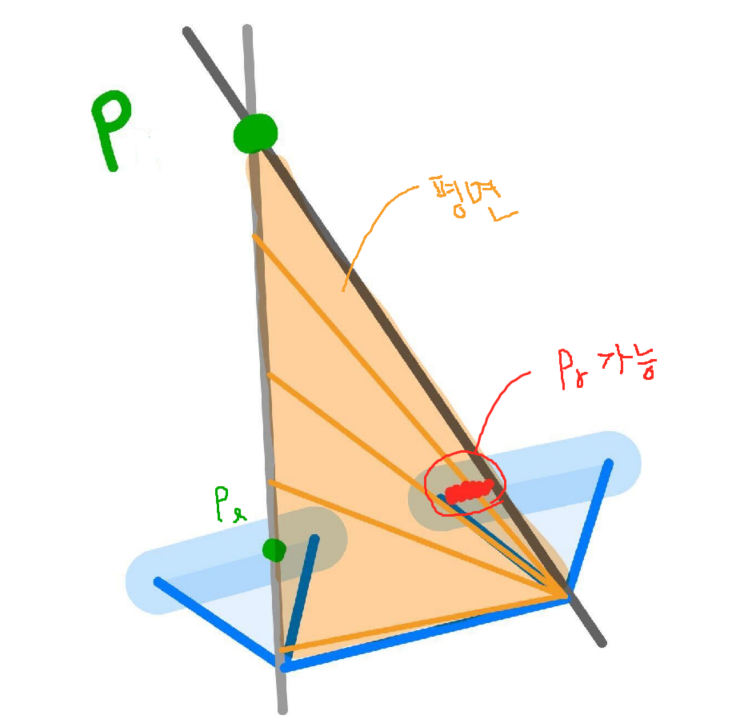
bundle adjustment 이후, 3D 포인트가 다시 투영되는데, 크기가 조정되지 않은 좌표가 왼쪽 프레임에 표시되므로 올바른 위치로 reprojectiohn되지 않을 가능성이 높다. Y축에 대해서는 스테레오 대응 이미지의 위치가 동일하지만, X축에 대해서는 모호하다. 따라서 누락된 스케일링 파라미터를 구하기 위해 feature간의 유사성을 극대화한다. 아래의 식으로 작성할 수 있으며, MI는 픽셀의 강도가 아닌 likelihood이다. 즉, 가능성이 최대가 되는 λ를 찾는 것이다.
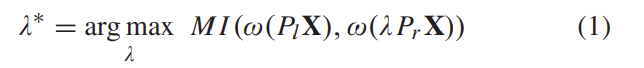
\mathbf{X}는 feature의 3D 위치, \omega는 이미지의 특정 위치에서의 window operator이다. 이때 하나의 픽셀만 이용하는 것은 부정확할 수 있으므로, window를 이용하여 MI를 위한 삼각측량의 정확도를 높인다. 이를 확장하여 N개의 point에 대한 M stereo pose에 대한 식을 구하면 아래의 식으로 표현할 수 있다.
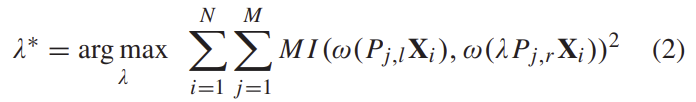
이때 P_{j,\left\{l,r\right\}}는 keyframe 에서 projection matrix이고 \mathbf{X}_i는 i번째 3D 포인트이다.
특징이 덜 두드러질 경우 유사성을 찾기 어렵다는 문제가 발생하며, multispectral local matching의 경우 더 많은 특이치와 편향된 motion 추정이 발생하게 된다.
추정 기반의 bundle adjustment는 추정이 적절하다고 가정하고 이전 카메라의 pose를 기반으로 motion을 계산하므로, 현재에 얻은 새로운 카메라 pose와 3D 포인트도 스케일링 된다. 즉, stereo 쌍에 대해 3D포인트는 두 이미지의 올바른 위치에 투영되어야 한다.
스케일링 파라미터는 초기에 1로 사용할 수 있으나, 노이즈에 의해 1이 되지 않는다. 따라서 오류가 누적되어 상당한 오차가 발생할 경우 스케일 최적화 프로세스는 stereo setup을 이용하여 이를 완화한다.
scale recovery 알고리즘의 성능 향상을 위해 몇가지 조정이 필요하다. 우선 거리상 가까운 feature는 scale 변화가 크므로 objectivefunction에 큰 기여를 하며, 대부분이 최신 프레임에 있다.
least-squares 최적화 방식에서, 다른 파라미터의 공분산 행렬은 최적의 상태에서 Hessian matrix의 역수를 계산하여 얻을 수 있다. 각 최적화는 독립적이기 때문에 local window에서 각 iteration마다 pose의 공분산이 계산된다. 첫번째 pose 추정치와 그에 대응되는 6×6 공분산 행렬을 얻은 뒤, 스케일이 계산되어 pose를 스케일링하는 데 사용한다. scaling transformation으로 나타내면 다음과 같다.
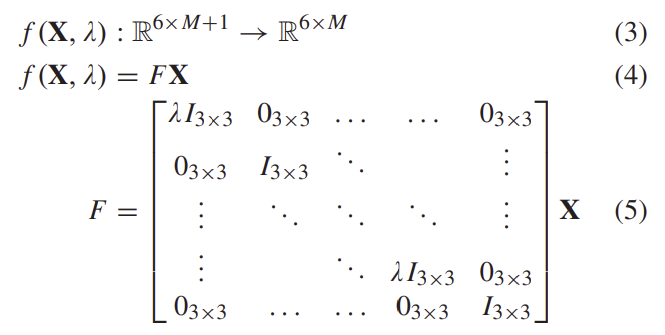
pose 공분산은 단순히 scale variance를 곱할 수 없으므로, augmented P는 다음을 통해 구할 수 있다.
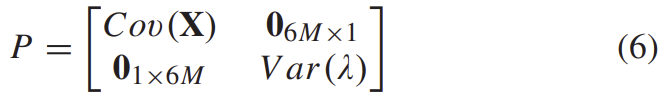
스케일링된 pose의 공분산은 linear transform을 적용하여 구한다.

Multispectral Visual-Inertial Navigation System
visual-inertial odometry(VIO)에서 loosely-coupled 방식을 적용하는 것은 visual 센서의 정보와 inertial 정보를 독립적으로 처리하여 pose를 추정한 후 이를 융합하는 방식을 의미한다. 이 논문에서도 loosely-coupled 방식을 적용하였다. (tightly-coupled 방식은 camera poses, feature positions, IMU 파라미터를 동시에 최적화하는 방식으로 상관관계가 높아지도록 할 수 있지만 다르 센서와 융합하기 어렵고, 구현이 어렵다는 단점이 있다.) 이는 VO 알고리즘을 크게 변경하지 않고 inertial 저보를 통합할수 있다는 장점이 있으며, extreme한 상황에서 견고성을 가질 수 있어 sensor failure 상황을 잘 관리할 수 있다.
이 논문은 Error-State Extended Kalman Filter(ESEKF)** 방식에서 영감을 받았으며, 절대 및 상대 pose를 기반으로 두가지 측정 모델을 도출한다.
*** A. Beauvisage, “Robust multispectral image-based localisation solutions for autonomous systems,” Ph.D. dissertation, Dept. Electron. Warfare, Inf. Cyber, Cranfield Univ., Cranfield, U.K., 2019*
*** D. Simon, Optimal State Estimation. Hoboken, NJ, USA: Wiley, May 2006. [Online]. Available: http://doi.wiley.com/10.1002/ 0470045345*
A. State Modeling
앞의 GMS-VO에서 설명한 방식으로 scale recover이 된 VO로 새로운 pose가 생성되면 state와 공분산이 모두 수정되고, state vector는
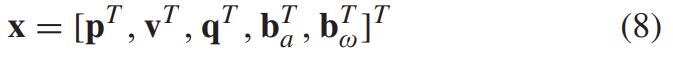
가 되며, 이때 q는 차량의 방향에 대응되는 사분원, p,v,b_a,b_w는 각각 차량의 위치, 속도, 가속도 bias, 자이로스코프 bias에 해당하는 3D 벡터이다.
error-state filter는 Extended Kalma Filter(EKF)와 비교하였을 때 다음 3가지의 장점이 있다.
- 시스템의 모든 dynamics를 추정에 포함하므로 큰 신호의 오류를 감쇠시킬 수 있다.
- 오류가 항상 작고 천천하 변화한다. ⇒ linear 오류가 감소 & 고차 항을 무시할 수 있어 계산 속도↑
- 방향 오류를 최소 형태로 매개 변수화 할 수 있다.
따라서 3가지 구성요소를 포함하는 3D rotatoin vecor δθ를 방향 오류를 나타내기 위해 사용하며, 이러한 오류는 사분원의 차로 표현된다.
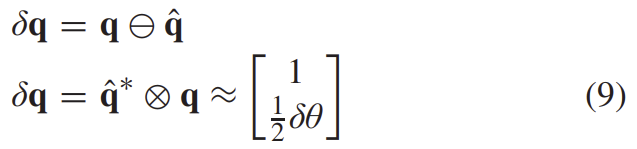
error-state는 아래와 같이 모델링할 수 있다.
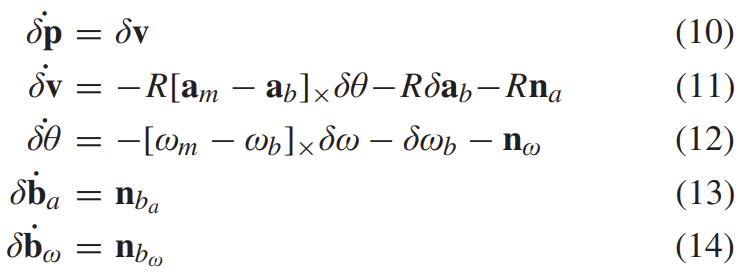
B. Process Model and Error Propagation
앞서 구한 공식(10)-(14)는 아래의 선형 형태로 나타낼 수 있다.
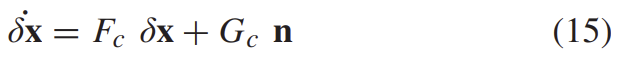
n=[n^T_a,n^T_{b_a},n^T_w,n^T_{b_w}로 각각 가속도계, 가속도계 bias, 각속도, gyroscope biase noise에 해당한다. 이는 IMU 센서 제조업체로부터 얻은 파라미터이고, 두 상태 사이의 discrete-time 업데이트를 위해 위의 식(15)는 아래와 같이 통합된다.
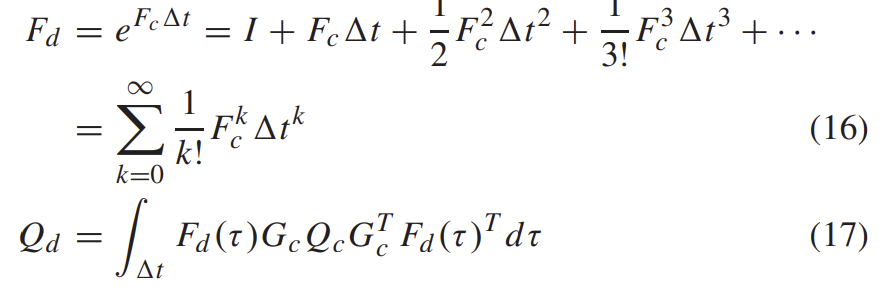
Q_d = diag(n)은 continuous time의 공분산 행렬이고, F_c와 G_c는 시간 간격 t에서 일정하다고 가정한다. 이렇게 하면 F_d와 Q_d를 빠르게 구할 수 있고, state와 공분산은 다음과 같이 IMU 측정 u_k로 propagate 된다.
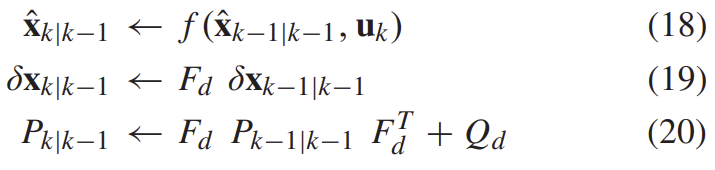
C. Measurement Model
VO는 차량의 현재 state와 자세에 대한 부분적 정보를 제공하고, 여기에 불확실성을 의미하는 Gaussian noise v도 포함된다. 따라서 측정된 모델은 아래의 식과 같이 정의할 수 있다.
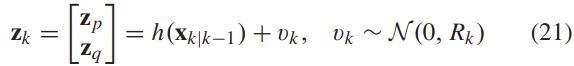
z_k는 keyframe k에서 추정되며 R_k는 측정 노이즈 속성에 맞게 골라야합니다. (*\mathcal{N}은 노이즈와 관련된 항으로 이해하면 될 것 같습니다.) 이를 통해 최적화 프로세스에서 공분산을 계산할 수 있고, 이는 식(7)의 P'에 해당합니다.
식 (21)로부터 error 관찰은 아래의 식으로 정의된다.
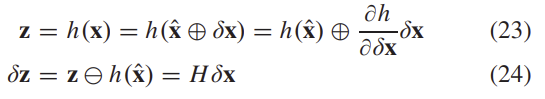
이때 δz는 error-state의 선형 조합으로 표현되고, 오차 사분원이 최소 형태로 표현될 때 H는 다음과 같다.
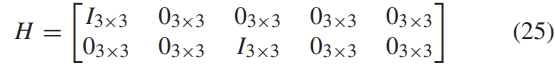
1) 절대 카메라 좌표
state 수정에 사용되는 첫번째 측정값은 VO 궤적에서 추출된 절대 카메라 pose이다. 이는 독립적인 VO 알고리즘에 의해 계산이 되며, 관측 모델은 다음 식이 된다.
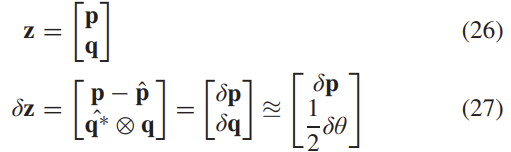
2) 상대 카메라 좌표
공분산은window를 통해 측정이 되므로, 이를 일관되게 사용하기 위해서는 k-n단계에서 window의 마지막 pose가 k단계에서 window의 첫번째 pose일 경우, k단계의 마지막 window pose 추정치를 이용하여 현재의 state를 수정해야 한다. 이를 통해 VO 측정값이 독립적으로 얻어진다.
또한 z는 추정된 window의 첫번째 pose에 대한 VO포즈를 나타내므로, 절대촤표계의 추정치와 직접 비교할 수 없다. 따라서 IMU 통합 이전에 수정된 state \mathbf{x}_{k-1|k-1}의 duplication이 생성된다.

상대 transformation \mathbf{z}는 \mathbf{x}'_k가 적용되어 다음의 식이 된다.
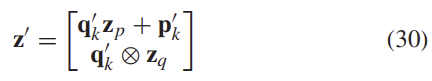
VO pose를 함께 propagating하는 대신, 상대 측정값을 이용하여 state를 증가시킨다. 일관성을 유지하기 위해 새로운 측정치의 공분산 R'는 다음과 같이 propagation된다.
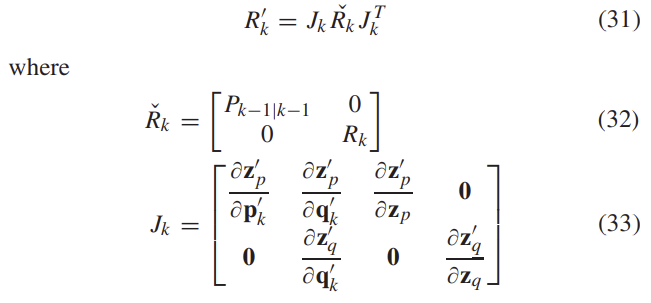
D. Correction and Reset
오류가 관찰되기 전의 innovation term과 공분산은 다음과 같이 표현된다.
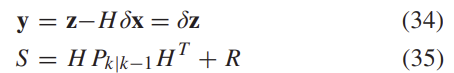
이를 이용하여 error-state를 수정하는 데 이용할 수 있고 이는 아래와 같이 표현된다.
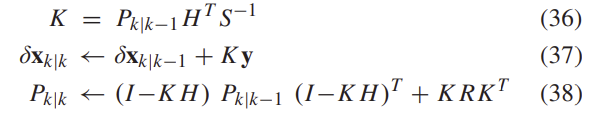
상대적 측정값 업데이트는 앞의 C 섹션에서 설명한 형태 \mathbf{z}'로 계산된다.
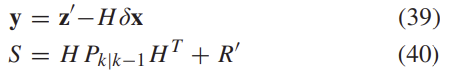
error-state가 관찰되고 수정된다면, 이는 prediction state에 주입되고, 다시 0으로 리셋된다
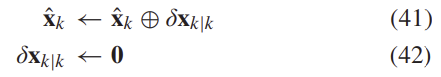
Experimental Validation

제안된 방식의 유효성과 성능은 그림 3과 같이 multispectral stereo setup으로 차량에 설치하여 획득한 다양한 데이터셋에서 평가된다. 하드웨어적으로 동기화를 맞추었고, 이미지는 30Hz로 획득하였다. 카메라와 관련된 설정 및 setup이 추가로 궁금하신 분은 논문을 직접 확인해보시면 좋을 것 같습니다.
이 논문의 GMS-VO 방식은 LMS-VO***라는 local matching 방식과 비교된다. 또한 GMS-VO가 다른 visual-thermal 방식과 비교된다.
*** A. Beauvisage, N. Aouf, and H. Courtois, “Multi-spectral visual odometry for unmanned air vehicles,” in Proc. IEEE Int. Conf. Syst., Man, Cybern. (SMC), Budapest, Hungary, Oct. 2016, pp. 1994–1999. [Online]. Available: http://ieeexplore.ieee.org/document/7844533/
A. Multispectral Visual Odometry
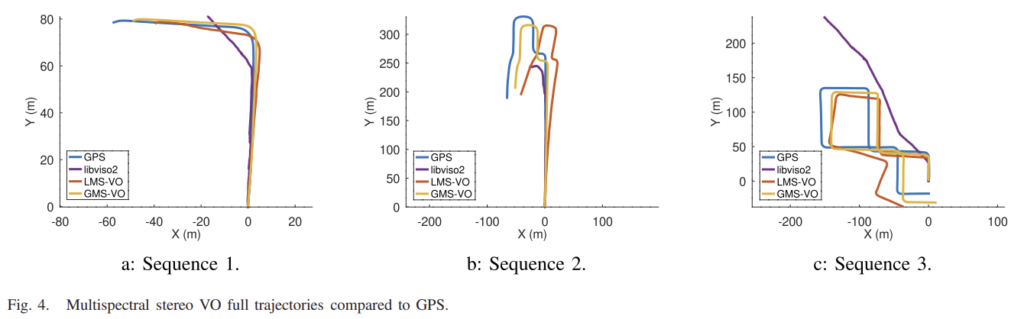
제안된 VO 방식의 성능은 LMS-VO, libviso2(SOTA), GT인 GNSS와 비교하여 평가한다. 오차는 각 iteration에서 추정된 카메라의 2D 위치와 해당 GNNS 위치 사이의 유클리드 거리를 기반으로 계산된다. 그림4는 GMS-VO도 약간의 drift가 있고 항상 scale이 정확히 복구되지 않더라도 GMS-VO가 GT와 더 유사하며, LMS-VO는 조금 더 옆으로 drift 된 것을 확인할 수 있다. 이는 GMS-VO가 2D에서만, 그리고 여러 프레임을 이용하여 motion을 추정하기 때문이다. 상대 방향과 unscaled translation은 이를 통해 더 정확하게 구해지며, 오차의 주요 원인은 scale 추정이기 때문이다. LMS-VO는 3D-to-2D motion 추정에 의존하고, 이는 multispectral 이미지 사이의 대응점을 차는 것이 정확하지 않기 때문에 어려운 것이다. 또한 multispecgtral을 intensity-based matching 방식인 libviso2과 비교했을 때 multi-spectral 이미지에 대처하기 어려움을 확인할 수 있다.

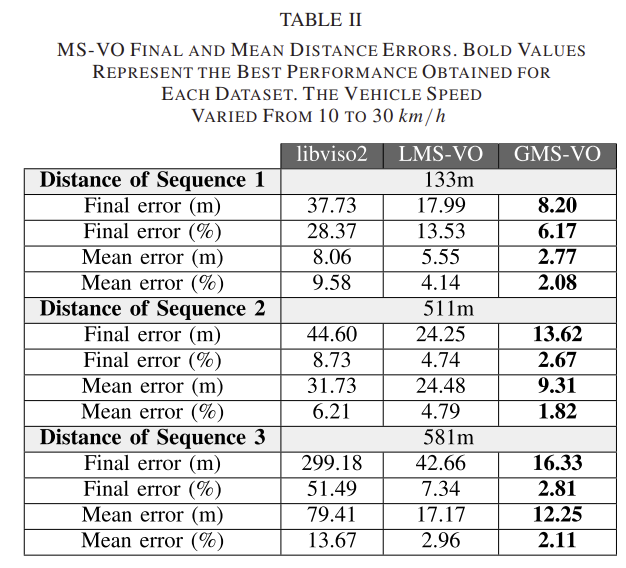
그림 5는 연속 keyframe간의 상대 오차로 LMS-VO와 GMS-VO에 대한 결과를 시각화한 것이다. 표 2에도 표현되었으며, 표 5에는 libviso2에 대한 결과도 포함되어있다. 그림 5는 각도가 크게 변하는 위치의 개수만큼 그래프의 피크가 있는 것을 확인할 수 있다. 즉, 회전이 생길 때 상대 오차가 커지는 것으로, 이는 모션 블러가 원인일 수도 있고, 광학적 변화가 커 추적되는 feature의 수가 줄었기 때문일 수도 있다. 그림 5를 통해 GMS-VO가 LMS-VO보다 대체로 정확한 것을 확인할 수 있다.
또한, 표2를 통해 GMS-VO방식과 LMS-VO방식과 비교했을 때 libviso2 라이브러리 성능이 떨어지는 것을 통해 픽셀의 강도에 의존하는 방식을 태체할 기술이 필요하다는 것을 확인할 수 있다.
B. Multispectral Visual-Inertial Navigation(MS-VINS)
1) Absolute Measuremants
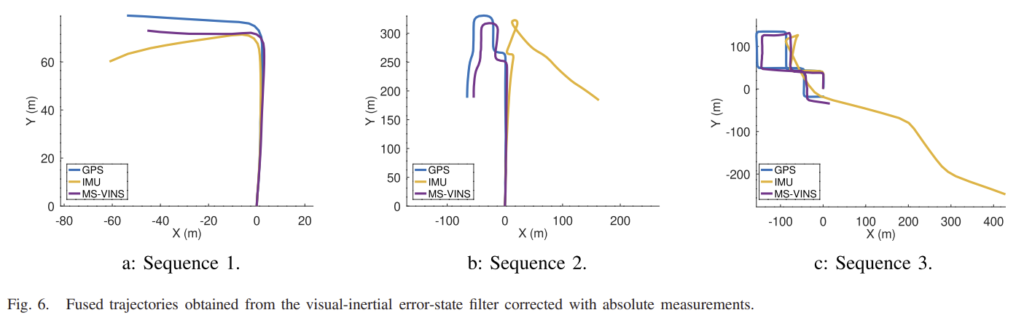
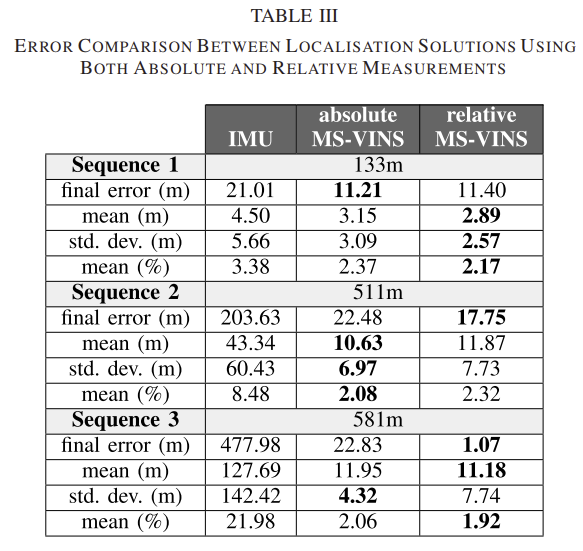
그림 6의 MS-VINS는 GMS-VO로 얻은 절대 카메라 좌표 정보와 IMU정보가 융합된 결과로 필터링을 통해 얻은 IMU를 통합하여 얻은 결과보다 GT와 더욱 유사한 것을 확인할 수 있다. 표3의 error 분석에 의하면 IMU로 구한 결과가 큰 오차를 가져오는 것을 확인할 수 있다.
또한, 궤적이 길고 복잡한 sequence 3의 평균 오차가 2.06%이고, 비교적 짧고 단순한 sequence 1이 2.37%의 평균오차를 가지는 것을 통해, 궤적이 길고 복잡할 수록 IMU에 GMS-VO보정이 더욱 많이 되는 것을 알 수 있다.

이는 IMU 데이터가 수정되지 않을 경우 error가 지속적으로 증가하기 때문으로, 그림 7을 통해 상대 오차가 점점 증가되는 것을 확인할 수 있다. 그러나 MS-VINS의 경우는 오차가 수정되어 b와 c에서 오차정도가 줄어드는 것을 알 수 있다.
2) Relative Measurements
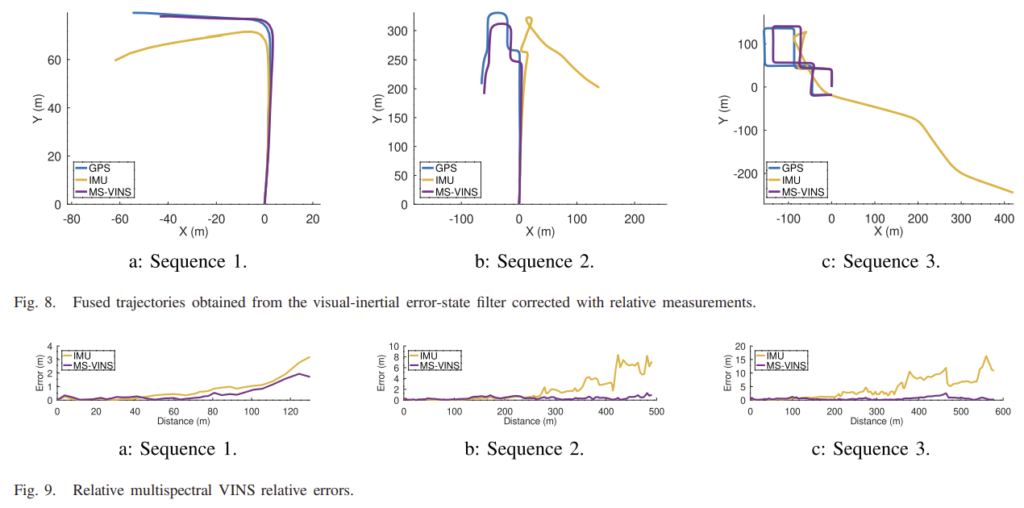
그림 8을 통해 relative transformation과 local 공분산이 데이터 fusion에 일관성을 향상시키는 것을 알 수 있다. sequence 1의 회전 이후에 absolute measurement는 상당히 drift되었지만, 그림 8에서는 이러한 drift 문제가 제거되었다.
C. Failure Recovery
multispectral setup의 장점은 특징의 추적과 matching이 실패했을 때 다른 촬영 장비를 이용할 수 있다는 것으로, extreme한 조명 조건과 외부 요인에 더 강인하게 한다. 그러나 두 촬영장비의 추정치가 모두 실패할 경우(그림 12)는 복구가 어렵고, 이를 위해 제안된 방법이 window bundle adjustment를 기반으로 하여 매칭되는 항목이 부족하면 VO를 중단하고 전체를 다시 초기화한다. 이 단계를 통해 몇개의 frame을 활용할 수 없고, 이는 VO 궤적 추정에 영향을 줄 수 있다. 따라서 relative measurement를 이용하는 방식이 선호된다.
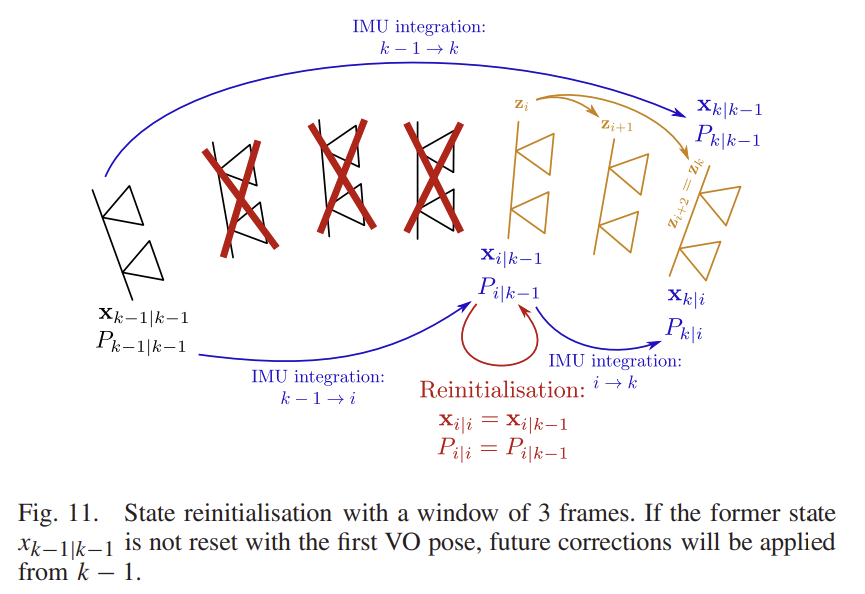
그림 11과 같이 측정값이 전달되지 않을 경우 \mathbf{x}_{k|k-1}, P_{k|k-1}로 전파된다. 그러나 incremental 방식은 failure 전의 마지막 보정 상태로 \mathbf{x}_{k-1|k-1}, P_{k-1|k-1}를 이용하면 안된다. 대신 keyframe을 선택할 때 incremented measurement \mathbf{z}'를 생성하는 데 사용된 state는 i단계에서 다시 초기화해야하고, 그림 11에서 확인할 수 있듯이 k-1과 i사이에 보정은 measuremen가 제공되지 않았으므로 \mathbf{x}_{i|k-1}은 단순히 \mathbf{x}_{i|i}가 되고 \mathbf{z}'는 \mathbf{x}_{i|i}를 기반으로 계산된다.
즉, k-1과 i사이의 motion은 보정되지 않는다.

이러한 robustness는 시각적 정보를 활용할 수 없는 시나리오에서 테스트되며 VO를 다시 초기화해야한다. 첫번째 sequence는 빠른 회전에 의해 영향을 받아 motion 블러가 생긴 경우이다. 다른 sequence는 VO의 반복적인 벽의 geometry가 feature 추정을 어렵게 하는 경우로, 이에 대응되는 이미지가 그림 12이다.
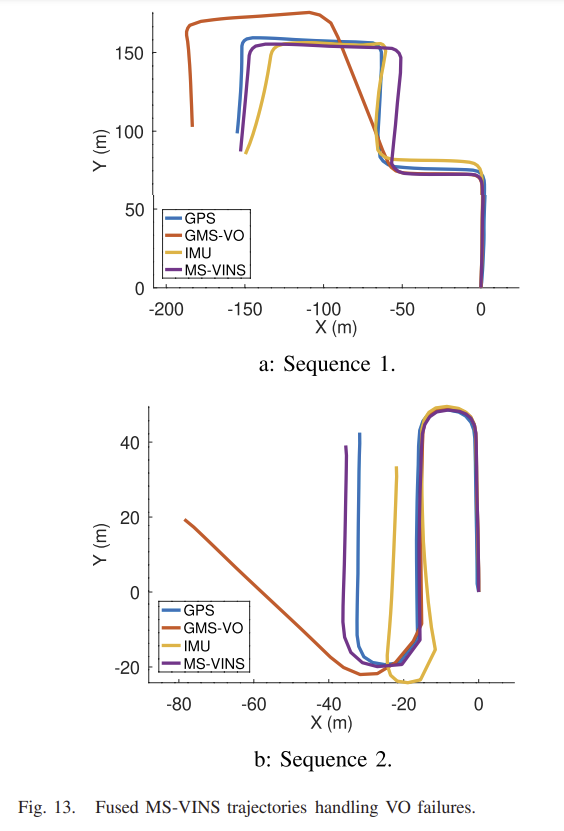
결과는 그림 13에 나타나고, 두 sequence 모두 VO가 실패하지 않ㅎ았던 이전의 데이터셋과 비교했을 때 GMS-VO궤적이 GT와 큰 차이가 나는 것을 확인할 수 있다. 이는 VO가 오류를 수정할 수 없기 때문으로, IMU의 경우 비교적 잘 예측된 것을 확인할 수있으며, VO가 잘 작동하지 않은 경우 IMU가 신뢰할 수 있을 만큼의 state를 추정하였다는 것을 알 수 있다.
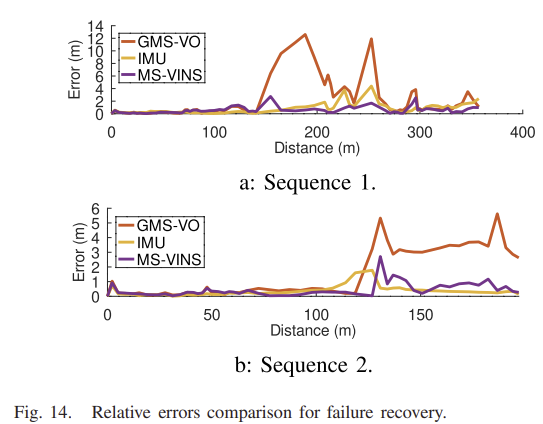
이에 대한 상대 오차는 그림 14에서 확인할 수 있으며, sequence 2는 1번의 고장이 있고 이후 VO 오차 높게 유지된다. 그러나 sequence 1은 2번의 고장이 있고, 두번째 이후에 오차 정도가 줄어드는 데 이는 두번째 고장이 이를 보완하기 때문이다.
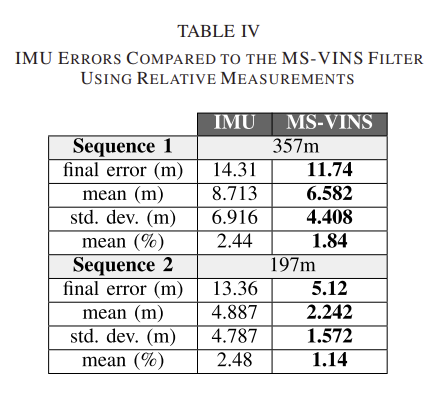
표 5에 결과를 리포팅하였으며, IMU가 융합된 경우에 pose 추정 성능이 향상된 것을 알 수 있다. 표3의 relative MS-VINS와 비교했을 때 필터를 이용하여 생성된 궤적은 mean (%) 2%미만의 오류를 만들었고, 이는 failure가 발생하지 않은 경우에 달성한 경우와 같다. 특히 sequence 2의 경우 필터링된 궤적을 통해 1.1%의 최소 오차를 얻었다.
해당 연구를 통해 multispectral VO를 칼만필터를 사용하여 IMU 센서와 융합할 수 있으며, 짧은 failure상황을 보완할 수 있음을 보였다.