[CVPR2022]Unsupervised Homography Estimation with Coplanarity-Aware GAN

이번에 소개드릴 논문은 CVPR2022년도에 나온 Homography Estimation 논문입니다. 해당 논문의 가장 큰 특징들이 제목에 키워드로 나와있는데, 일단 Unsupervised 기반으로 Homography를 추정하는 방법론이며 이때 Coplanarity-Aware GAN이라는 새로운 학습 방법을 제안하는 논문입니다.

Intro

먼저 Homography는 영상을 기본적으로 다루는 분들이라면 모두들 알고 있을 것이라고 생각되기에 간략하게 설명하겠습니다. Homography는 평면 물체의 2차원 영상과 영상 사이에 투영 변환 관계를 나타내는 행렬로 이러한 Homography Estimation은 Image stitching, camera calibration, SLAM 등 정말 다양한 분야에서 활용이 됩니다.

특히 Image Registration 분야에서 호모그래피를 활용해 두 영상 사이의 정합을 맞추려는 연구들도 상당히 많이 존재를 하고 있습니다. 가장 흔한 방법으로는 SIFT와 같은 특징들을 추출한 다음(feature extraction) 두 영상 사이의 특징들이 서로 같은 특징인지 매칭하여(correspondence matching) 최종적으로 대응되는 포인트들을 가지고 DLT 또는 RANSAC 알고리즘을 통해 호모그래피를 계산할 수 있습니다.

하지만 이러한 방법론들은 연산 과정이 상당히 느리기도 하고 특징이 잘 뽑히지 않는 textureless 영역들에 대해 상당히 취약한 것으로 알려져있습니다. 최근에는 DNN을 활용해 homography를 추정하는 연구들이 제안되고 있는데, 이에 대한 내용들은 김지원 연구원님이 작성한 리뷰들을 참고해주시면 좋을 것 같습니다.

아무튼 이러한 딥러닝 기반 호모그래피 추정 방법론들은 상대적으로 textureless한 영역에서도 강인하고 속도도 빠르다는 장점이 있지만 전체 영상에 대한 Image Registration은 수행하지 못합니다.

애초에 Image Registration 분야에서 호모그래피를 통해 완벽하게 픽셀레벨로 정합을 맞추는 것은 불가능에 가까운데, 이는 호모그래피의 조건이 바로 “평면 물체”에만 올바르게 동작하도록 설계된 행렬이기 때문입니다.

즉 저희가 촬영하는 이미지는 평면이 아닌 입체가 뚜렷한 3D 물체를 촬영한 것이며 또한 3D 물체가 영상으로 촬영될 때 2D로 투영된다 하더라도 결국 원근에 따라 전경과 후경이 나뉘는 등의 이유로 하나의 호모그래피로는 영상 전체에 대해 정합이 불가능하게 됩니다.

아무튼 이러한 한계 때문인지는 몰라도 DNN 기반 호모그래피 추정 방법론들은 다중 평면이 있는 영상을 정합하기 위한 호모그래피를 구할 때 학습 가능한 마스크(일종의 inliner 마스크)를 활용하여 어떤 픽셀들을 가지고 추론하는 것이 정합을 더 잘할 수 있는지에 대해 학습/추론 하게 됩니다.

하지만 이러한 방법들은 명확한 가이드를 주기에는 부족하다고 저자는 주장하고 있으며 더 나아가 plane-induced parallax를 다루지 못한다고 주장합니다.

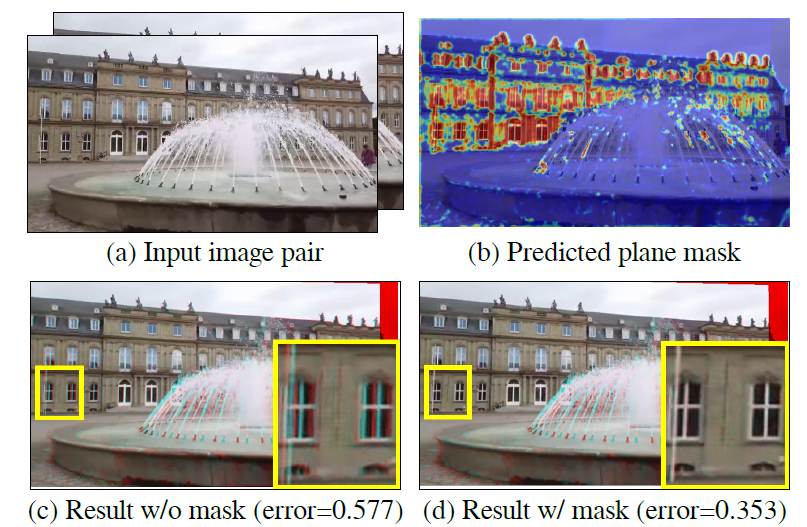
그래서 저자는 전체 영상 대신에 지배적인 평면(dominant plane)에 최대한 집중하여 호모그래피를 추정하는 방법론을 제안한다고 합니다. 즉 저자는 하나의 호모그래피로는 영상 전체에 대해 정합을 수행하는 것은 불가능하다는 것을 먼저 인정하기에, 예측된 호모그래피로부터 각 픽셀들이 얼마나 잘 정합이 맞았는지에 대하여 확인할 수 있는 마스크를 추정하려고 합니다.

즉 이렇게 추정된 마스크는 일종의 domiant plane이 무엇인지를 판단하는 마스크로 이는 곧 입력 영상 속에서 어떤 영역들이 서로 동일한 평면인지를 알려준다고 생각하시면 되겠습니다. 이렇게 추정된 마스크는 모델 학습시에 추가적인 coplanarity constraint와 area penalty를 제공할 수 있다고 합니다.

그리고 이러한 마스크를 취득하기 위해서 저자는 HomoGAN이라는 방법론을 새롭게 제안합니다. 이는 먼저 Homography estimator에게 dominant plane을 가이드하기 위해서 Unsupervised GAN을 활용해 한 쌍의 feature map으로부터 서로가 정합이 맞는 영역에 대한 soft mask를 추출하게 됩니다.

또한 저자는 트랜스포머 구조를 이용해 Coarse-to-Fine 형식으로 homography를 추정하고자 하였습니다.

위의 내용이 정리해보니 어수선한 것 같아 요약하자면 아래와 같습니다.

1. 실세계에서 취득된 정합이 맞지 않는 영상은 하나의 호모그래피로 전체 영역을 모두 정합시킬 수 없다.(하나의 호모그래피는 하나의 동일 평면위의 점들 사이에만 유효(호모그래피의 Coplanarity 성질)하지만 대부분의 영상은 2개 이상의 평면들이 존재로 함.)
2. 그래서 저자는 영상에서 가장 지배적인 Coplanarity 영역을 보여주는 Coplanarity Mask를 추정하기 위핸 Coplanarity-Aware GAN을 제안함.
3. 덤으로 Transformer 기반의 Homography estimator도 제안함.

Method

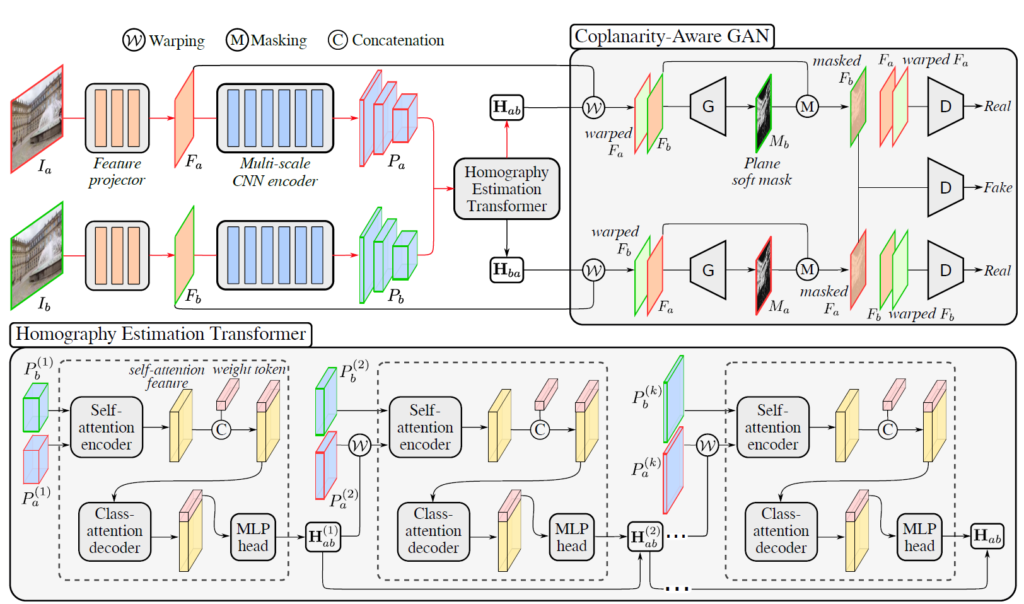
일단 해당 논문의 전체 학습 과정 및 구조는 그림2에서 확인하실 수 있습니다. 먼저 한 쌍의 정합이 맞지 않는 영상( I_{a}, I_{b})이 각각 3개의 컨볼루션 레이어를 통과합니다. 이는 기존의 Unsupervised Homography Estiatmion 방법론들이 많이 활용하는 Feature projector로 입력 영상의 조도 변화가 큰 것을 의식해 feature level로 투영하는 과정을 의미합니다.

그 후 Multi-scale CNN Encoder를 통과하여 서로 다른 해상도를 가진 k개의 encoder feature를 생성합니다. 해당 논문에서는 k는 3으로 하였으며 각각의 해상도는 2배 차이가 납니다.

그리고 나서 저자가 새롭게 제안하는 Homography Estimation Transformer에 입력을 넣어 호모그래피를 계산하게 됩니다. 호모그래피를 추정하는 방법에는 크게 2가지로 Homography의 8개 파라미터를 바로 regression 하는 방법, 4쌍의 offset을 계산하여 DLT 알고리즘을 통해 호모그래피로 변환하는 보다 간접적인 방법이 존재합니다.

여기서 전자의 방식의 경우 가장 흔하고 일반적으로 생각할 수 있는 방법이지만, 딥러닝 기반의 호모그래피 추정 방법론들은 아무도 전자의 방법을 사용하지 않고 대부분 후자의 방법을 사용합니다. 이는 호모그래피의 3×3 행렬 안에는 translation, rotation, scale, 닮음 등 다양한 성분들이 존재하게 되는데 이 성분들의 scale variation이 크게 존재하여 모델 학습 시 안정적이며 정확한 호모그래피를 추정하기 어렵다고 합니다.

그래서 대부분 후자의 방법으로 offset을 구하는 식으로 학습하게 되는데, 해당 논문에서는 이러한 offset이 아닌 flow 기반의 homography 추정 방법을 사용하였다고 합니다. 이는 ICCV2021 논문 중에 호모그래피의 8개의 파라미터 성분을 각각의 flow map으로 표현하는 homography flow라는 방법론이 있는데 해당 방법론을 그대로 적용한 것 같습니다(해당 논문은 김지원 연구원님이 예전에 리뷰하였기 때문에 참고하시면 좋을 듯 합니다.)

아무튼 이렇게 추정된 Homography를 통해 I_{a}, I_{b}에 대하여 다양한 조합으로 warping을 수행한 후 Coplanarity-Aware GAN을 통해 Plane-soft mask를 추정 및 학습에 활용하게 됩니다. 보다 자세한 내용들은 아래에서 다루도록 하겠습니다.

Homography Estimation Transformer

먼저 HET(Homography Estimation Transformer)에 대해서 살펴보겠습니다. 해당 모듈의 구조는 그림2 아래에서 확인하실 수 있다시피, Self-attention encoder -> concatenate weight token -> Class-attention decoder -> MLP 과정을 통해 호모그래피를 구할 수 있게 됩니다.

여기서 Self-attention encoder는 Swin Transformer를 활용하였다고 합니다. 모든 모듈에서 입력 feature map을 다운샘플링하는 patch merging layer은 i-1개 사용되었으며 이를 통해 self-attention의 output feature의 차원이 2C_{1} \times (H_{1}W_{1}) 가지게 됩니다.

그 다음은 Class-attention decoder에 대한 설명으로 Class-attention decoder를 통과하기 바로 직전에 먼저 학습 가능한 weight token( 2C_{1} \times 8 )을 self-attention feature에 concat해주어 2C_{1} \times (H_{1}W_{1} +8) 의 결과를 생성합니다.

그 후 class-attention sub-block의 입력으로 태움으로써 weight token과 self-attention feature 사이에 attention score를 계산한다고 합니다. 이를 통하여 weight token이 모든 패치의 정보를 수집하여 호모그래피 플로우의 weight 값을 추정하는데 있어 도움이 된다고 하는데 음… 일단 class-attention decoder에 대한 구조 및 관련 개념을 잘 모르기도 하고 concatenation이 어떤 관점에서 aggregation 역할을 한다는 지는 제 머릿속으로 크게 와닿지가 않습니다.

아무튼 이 후에 2개의 FC layer로 구성된 MLP를 통과하여 최종적으로 길이가 8인 weight vector를 추정하게 되면 i-th module에 대한 호모그래피 결과를 생성하게 된 것입니다.

그림2 그림을 다시 살펴보시면 HET는 Fine-to-Coarse의 계층적인 구조로 Homography를 계산하는 것을 확인하실 수 있습니다. 즉 첫번째는 제일 마지막 인코더 스테이지의 feature map을, 제일 마지막 모듈은 제일 첫번째 인코더의 스테이지 feature map과 2번째 호모그래피 결과값을 활용합니다. 수식으로 표현하면 아래와 같습니다.

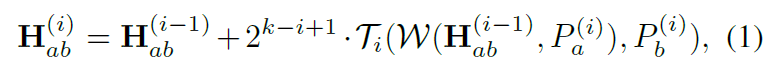
아무튼 계층적인 구조를 통해 Homography weight를 gradient boosting 기법처럼 계산하였다고 이해하시면 좋을 듯 합니다.

Coplanarity-Aware GAN

Intro에서도 장황하게 설명드렸다시피 논문에서 제안한 Coplanarity-Aware GAN은 HET가 호모그래피를 추정할 때 (비록 두 영상 사이에 multiple plane이 존재하더라도) 지배적인 coplane을 찾아서 가이드해주기 위한 네트워크라고 이해하시면 좋을 것 같습니다.

과정에 대해서 차근차근 설명하자면 먼저 예측한 H_{ab}, H_{ba}를 각각 F_{a}, F_{b}에 적용하여 warped feature map F'_{a}, F'_{b}를 생성합니다. 그 후 다양한 조합 (e.g. (F_{a}, F'_{a}) , (F_{b}, F_{a}) 을 만들어서 각 영역들이 얼마나 잘 정합됐는지를 Discriminator를 통해 판단하는 것입니다.

저자가 말하길 이상적인 상황에서는 aligned region은 장면 속 dominant plane에 모두 위치해있을 것이라고 합니다. 이를 실제로 적용하기 위해 저자는 generator network를 통해 한 쌍의 feature map 사이에 지역적 consistency를 확인할 수 있도록 하였습니다. 이게 무슨 말이냐면 Generator를 통해 두 feature map이 얼마나 alignment가 잘 되었는지를 나타내는 soft mask를 추론하였다고 이해하시면 됩니다.

Generator Network는 3개의 컨볼루션 레이어와 ASPP 모듈로 구성되어있다고 합니다. ASPP라는 모듈에 대하여 자세한 설명은 딱히 없고 논문에서 인용만 했기 때문에, 자세하게 설명드리지 않은 점 양해바랍니다.

아무튼 Generator를 통해 생성되는 마스크는 M_{a}, M_{b}로 각각 M_{a} = G(F_{a}, F'_{b}), M_{b} = G(F_{b}, F'_{a}) 를 통해 생성이 됩니다. 또한 저자는 discriminator를 통해 입력 쌍의 변환이 하나의 단일 호모그래피인 경우인지를 판별한다고 합니다.

위와 같이 설계한 이유에 대해 간략하게 소개드리자면, 일반적인 경우 호모그래피는 평면의 의해 고유하게 결정이 되는데, 이러한 관점에서 만약 M_{a}, M_{b} 의 전경이 dominant plane에 있다면, 이로 인해 결정되는 호모그래피 역시 고유하다는 것입니다.

즉 위와 같은 동기의 관점으로 Discriminator가 F_{a}, F'_{a} 와 F_{b}, F'_{b} 는 고유의 호모그래피( H_{ab}, H_{ba})를 가지기에 real case로 분류하고, maksed feature( M_{a}F_{a}, M_{b}F_{b}) 는 fake case로 학습을 하게 되면, 그리고 Generator는 이러한 Discriminator를 속이는 방향으로 학습하게 된다면 Generator는 Fa와 Fb 사이에 고유의 호모그래피를 가지는 즉 coplane한 영역에 대한 정보를 마스크로 생성해낼 수 있을 것입니다.

Discriminator는 7개의 컨볼루션 레이어와 GAP layer를 가지고 있으며 학습은 Wasserstein distance를 통해 real과 fake 쌍에 대한 discrepancy를 계산하여 학습한다고 합니다. 또한 gradient reversal layer를 적용하였다고 하는데 이것은 기존의 있는 방법이라 논문에서는 참조만 하였기에 어떤 기능을 하는지는 잘 모르겠군요.

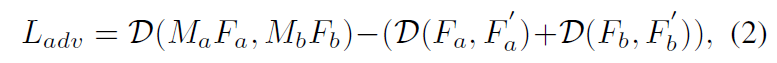
그리고 학습의 안정성을 위해 Discriminator에 대한 gradient에 패널티를 부여하였다고 합니다.

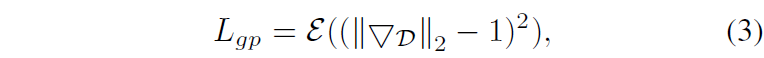
여기서 3을 거울 대칭한 모양은 평균을 의미하는 함수이며 역삼각형은 gradient 연산자라고 합니다. 마지막으로 두 마스크( M_{a}, M_{b} )와 constant mask( \hat{M} )에 대하여 cross-entropy loss를 계산하는 loss term을 추가하였는데 이는 ( M_{a}, M_{b} )이 coplanarity는 지키면서 더 큰 foreground를 가지도록 하는 loss라고 합니다.

최종적으로 GAN을 학습시키기 위한 loss는 아래와 같습니다.

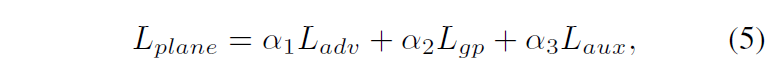
Network Training

앞서 설명드린 L_{plane} 말고도 추가로 Homography Estimation Transformer를 학습하는 loss에 대해서 다루도록 하겠습니다. 첫번째 loss는 기존의 DNN 기반 방법론들이 많이들 활용한다는 pixel-wise triplet loss를 그대로 사용합니다.

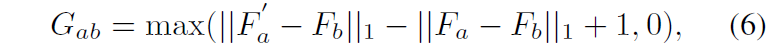
해당 loss의 의미는 a에서 b로 warping한 feature map F'_{a}와 실제 b의 feature map F_{b} 는 서로 positive로 보고, warping하지 않은 feature와 target feature는 서로 negative로 보고 margin은 1을 가지는 loss를 적용한 것으로 보면 됩니다.

다음은 alignment와 관련된 loss로 아래와 같습니다.

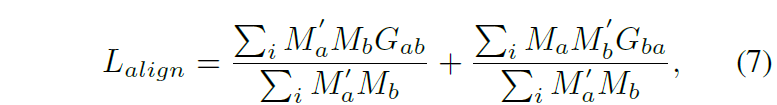
여기서 M' 는 warped mask를 의미합니다.

또한 마지막으로 warp-equivalent loss를 적용하였는데 해당 loss는 Image에 대하여 feature map을 먼저 추출한 다음 warping한 것과, 이미지를 먼저 warping하고 feature로 추출한 것과 서로 같도록 하는 loss로 이를 통해 feature가 luminance variation은 필터링하면서 geometric transformation은 계속 유지하도록 하였다고 합니다.

최종적으로 HET를 학습시키기 위한 loss는 다음과 같습니다.

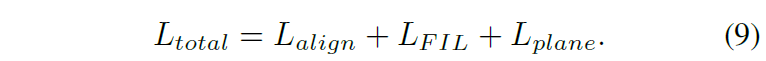
한가지 유의점은 해당 학습 방식(HET & GAN을 학습하는)은 two-stage로 동작하게 됩니다. 이는 기존의 Unsupervised Homography Estimation이 학습이 tripelt loss를 사용해서인지는 모르겠으나 상당히 불안정한데 더불어 adversarial training은 학습 불안정성의 가장 대표적이므로 이 둘을 동시에 학습할 경우 초기 학습이 진행이 안된다고 합니다.

그래서 초반에는 수식 9에서 L_{plane}과 L_{align}에서 수식7 부분을 제외하여 학습시킨 다음 어느정도 호모그래피가 안정적으로 추론되면 제외시켰던 loss 텀들을 추가하여 학습한다고 합니다.

Experiments

학습에 사용한 데이터 셋은 natural image dataset?이라는 것으로 약 75.8k의 학습데이터 셋과 4.2k개의 test data가 존재하는 데이터를 활용했다고 합니다. 영상 해상도는 320 x 640이며 데이터 셋은 크게 5가지의 카테고리로 구분되는데 regular(RE), low texture(LT), low light(LL), small foreground(SF), large foreground(LF)로 구분이 된다고 합니다.(그리고 맨 앞을 제외한 모든 카테고리들은 호모그래피를 추정하는데 있어 상당히 어려운 장면들이라고 이해해주시면 좋을 것 같습니다.)

또한 테스트데이터에는 6개의 매칭쌍이 GT로 제공되어있기 때문에 추정한 Homography를 통해 ground-truth point를 얼마나 잘 추론했는지를 학습할 수 있다고 합니다.

실험 비교대상으로는 전통적인 feature-based method들인 SIFT, ORB, BEBLID가 있으며 학습 기반의 feature based인 LIFT, SOSNet, SuperPoint 그리고 Deep learning based method(Supervised, Unsupervised, CA-Unsupervised, BasesHomo)를 비교하였다고 합니다.

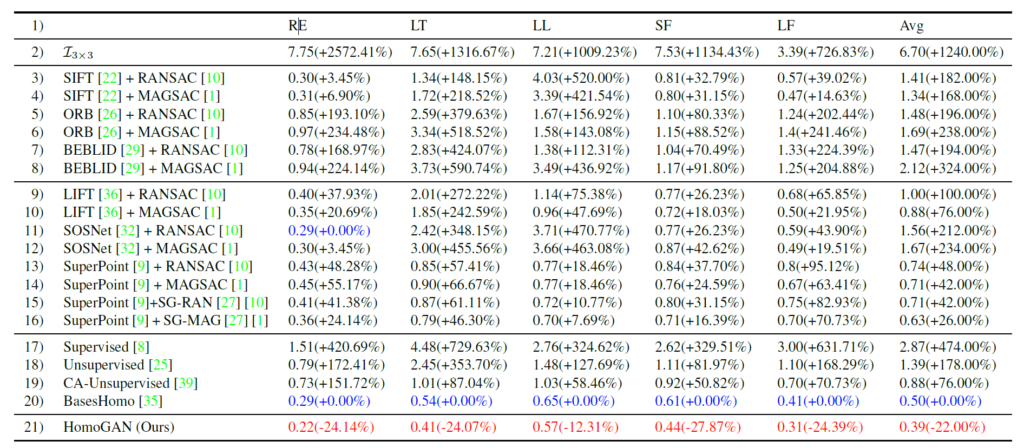
위에는 정량적인 결과 표를 나타낸 것입니다. 설명드린 대로 각각의 컬럼들은 데이터 셋의 case를, 그리고 avg는 5가지 케이스에 대한 평균 결과를 나타낸 것이며 평가 메트릭은 6개의 매칭 포인트에 대한 l2 distance의 평균입니다.

확실히 Feature based 방법론들이 일반적인 상황(RE)에서 좋은 모습을 보여주고 있는 반면에 textureless인 상황(LT)에서는 성능이 크게 감소하는 모습을 볼 수 있습니다. 물론 딥러닝 기반의 방법론들도 성능이 크게 떨어지고 있는데 해당 논문의 baseline으로 볼 수 있는 BasesHomo 방법론은 확실히 작년 Sota 논문이다보니 2번째로 모든 case에서 좋은 성능을 보이고 있습니다.

다음은 딥러닝 기반의 호모그래피 추론 방법론들끼리의 정성적 비교 결과입니다. 기존의 방법론들은 전경이 맞으면 배경이 틀어지거나 또는 그 반대의 양상을 보이는 반면에, 논문에서 제안하는 방법론은 다양한 평면에 대해서도 잘 추론했다는 점을 강조하고 있습니다.

이러한 양상은 feature based method와 비교해도 유효한 차이를 볼 수 있습니다.

특히 거리거 멀어 흐릿하거나 텍스쳐가 불분명한 상황에서도 논문에서 제안하는 방법론은 registration을 잘 수행하고 있다는 점을 강조하고 있습니다. 특히 3번째 열에서 지평선이 보이는 해안가 영상의 경우 keypoint를 뽑을만한 texture가 마땅히 없어서 타 방법론들은 호모그래피가 엉뚱하게 뽑혀 registration 결과가 엉망으로 나오는 모습이네요.

결론

나름대로 호모그래피의 고질적인 문제(하나의 호모그래피로 영상 전체를 정합할 수 없는)를 해결하기 위해 설계를 잘 한 것 같아서 좋은 논문이라고 생각이 되어집니다만 추론 속도는 타 방법론들과 비교하여 상당히 느리지 않을까 라는 생각도 조금 듭니다.(DNN 기반 방법론들은 단순한 CNN 인코더만을 활용하였을텐데 해당 방법론은 CNN encoder에 더불어 Transformer Encoder-Decoder가 들어간 block을 계층적 구조로 활용하기 때문에 속도측면에서는 많이 느리지 않을까 라는 생각이 있습니다.(참고로 해당 논문에서도 추론 속도에 대한 비교는 하지 않네요.)