이번 논문은 이벤트 카메라와 RGB(=frame=standard) 카메라 간 동일한 시점을 가질 수 있는 큐브 빔스플리트 시스템 구성과 이로 촬영된 데이터 셋을 제안하며, 저화질과 노이즈가 많은 이벤트 영상을 컬러 영상으로 보완하는 기법을 제안합니다.
Intro

이벤트 카메라는 빛의 변화가 발생한 픽셀에서만 정보를 취득하기 때문에 모든 픽셀의 빛 정보를 취합하는 전통적인 프레임 카메라에 비해 매운 빠른 촬영 속도를 보장받으며, 낮은 전력을 보장 받습니다. 또한 빛의 변화에 예민하게 반응하기 때문에 dynamic range의 크기가 매우 넓다(i.e. 저조도와 역광에 강인)는 특징을 가지고 있습니다. 특히, 빠른 촬영 속도를 보장 받기 때문에 블러 현상이 적게 발생한다는 장점을 가지고 있습니다.
이렇게 수많은 장점을 가진 이벤트 카메라는 비전 기반의 어플리케이션에서 큰 관심을 받고 있으며, 특히나 빠른 반응이 중요한 자율 주행, 로보틱스에서 많은 관심을 받고 있습니다. 하지만 비교적 개발된 시기가 짧은 이벤트 카메라는 여전히 낮은 해상도와 약간의 노이즈가 발생한다는 문제가 있습니다. (+근래에는 준수한 해상도의 이벤트 카메라가 개발되었습니다) 예를 들어, DAVIS240(; 2020년도에 활발히 활용된 센서)는 240 x 180 이라는 해상도를 가지고 있으며, fig 1- (a, b)에서 볼 수 있다시피 노이즈가 발생한다는 문제가 있습니다. 저자는 저해상도와 노이즈를 해결하기 위한 방법에 집중합니다.
저자는 이벤트 카메라의 두 문제점을 해결하기 위해 가시적 정보를 활용하는 두 도메인의 카메라를 상호 보완적으로 홀용하는 방법 guided event filtering (GEF; fig 1-(d)) 을 제안합니다. 또한, 두 도메인의 카메라의 시점을 일치 시키기 위해 큐브 빔스플리트를 이용하여 물리적인 정합을 진행한 시스템과 이를 이용한 데이터 셋을 제작 및 공개하였습니다. 마지막으로 저자는 해당 방법론의 효율성을 증명하기 위해 Motion deblur, Image reconstruction, Corner detection 실험을 진행합니다.
Method
Event sensing preliminaries
- frame-based camera로부터의 출력된 intensity(gray-scale) image I(x, y; t)
- event camera로부터 출력된 set of event \varepsilon = \{ e_{t_k} \}_{k=1}^{N_e} , where N_e 는 이벤트의 총 갯수
- 개별적인 이벤트 e_{t_k} = ( x_k, y_k, t_k, p_k) 는 4개의 상태값을 가짐
- x_k, y_k 는 공각적 좌표, t_k 는 시간대, p_k \in \{-1, 1 \} 는 polarity(빛의 감소, 증가를 의미)
- p_k = 1 if \theta_t > \epsilon_p, p_k = -1 if \theta_t < \epsilon_n
- where \theta_p = \log(I_t + b) - \log(l_{t - \delta t} + b) , b는 \log(0)로 발산하지 않도록 방지하기 위한 마진, [latex] \epsilon_p, \epsilon_n 는 각각 상승 혹은 감소에 따른 상수 임계값
+ 여기서 두 임계값 안에 위치한 부분은 변화가 발생하지 않았다고 판단합니다. - 저자는 시간에 따른 log intensity at time \mathcal{L}_t = \log(I_t + b)로 정의하여 이후 수식에서 활용하며, I, \varepsilon 는 같은 공간적 해상도를 가졌다고 가정
+ 명확한 표현을 위해 이벤트 카메라의 작동 방식을 수학적 표기로 정의한 파트로 보시면 됩니다.
++ 위의 내용을 쉽게 설명하자면 가까운 시간대에서 촬영된 각 intensity의 차이를 측정하고 임계값을 통해 이진 표현(polarity)으로 나타내는 방법 입니다. 이렇게 발생된 특징들이 이벤트에 해당합니다.
+++ 혹시나, log를 사용하는 이유에 궁금하신 분들은 '왜 로그 스케일을 사용하는가?' , 해당 블로그를 참고하시면 많은 도움이 될겁니다.
Event-intensity relation
위의 내용을 통해 이벤트 정보와 intensity/frame 정보는 시간적인 기울기(temporal-gradient)로부터 서로 연관되었다는 것을 알 수 있습니다. 이러한 관점에서 저자는 \mathcal{L} 의 시간적 기울기를 유도하기 위해 optical flow를 활용하고자 합니다.
우선 가까운 부근에 intensity가 같다고 볼 수 있는 지점에서의 small flow vector \delta\mathbf{u} = \[ \delta x, \delta y, \delta t \]^T 있다고 가정합니다. 그럼 이 가정은 수학적으로 표현하면 아래의 수식과 같습니다.
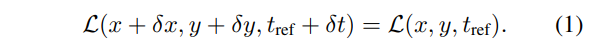
그럼 수식 1을 보다 쉽게 도식화하기 위해 1차항까지 근사한 테일러 급수로 정의하자면 다음과 같이 정의됩니다.
+ 유도 과정은 저도 이해를 못했습니다... 하하... 하지만 자료를 좀 찾아보니 컬러 영상으로부터 event generation model로 정의된 수식을 이용하여 다시 설명하는 것으로 확인하였습니다.
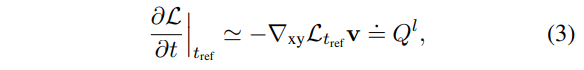
where \trangledown_{xy} \mathcal{L} 는 spatial gradient(e.g. sobel)를 의미하며, \mathbf{v} 는 velocity vector로 x, y에 대한 t의 미분에 해당합니다. Q^l 는 intensity image에서 파생된 시간적 기울기를 의미합니다.
+ 좀 풀어서 설명하자면 가까운 시점의 intensity 영상의 변화 정도를 정의 및 유도하기 위한 과정으로 보시면 됩니다. 결론적으로는 엣지 맵과 velocity vector로 가까운 시점의 영상의 변화 정도를 표현 가능하다는 주장입니다.
이벤트 정보 측면에서는 velocity v는 event간의 이동으로 볼 수 있습니다. 즉, 이벤트가 동일한 엣지에 의해 감지된다는 가정을 가질 수 있게됩니다. 따라서 시간적 기울기는 이동한 이벤트 간의 탄젠트로 해석 가능하며 이에 대한 수식은 다음과 같습니다.
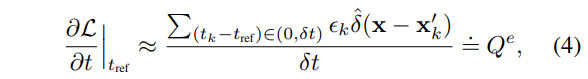
where \epsilon_k = \epsilon_p if p_k=1; and \epsilon_k = \epsilon_n if p_k = -1. \hat{\delta} 은 Dirac delta function, \mathbf{x}'_k = \mathbf({x}_k - (t_k - t_{ref})\mathbf{v} 는 t_ref 에 의해 와핑된 이벤트에 해당합니다. \mathbf{x} = \[x, y \]^T 에 해당하며, Q^e 는 이벤트에 의해 발생한 temporal gradient derived에 해당합니다.
+ 수식 4에 대한 풀이를 조금 하자면 Dirac delta function에 의해 와핑된 위치가 일치한 이벤트에 대해서 빛의 변화 정도를 측정하여 시간에 대해 미분한 결과에 해당합니다.
수식 3과 4는 각각 intensity image~image spatial gradients와 set of events에서 계산된 시각적 기울기에 해당하기 때문에 모든 값들이 이상적인 결과를 얻었다면 다음 수식과 같은 결과를 가져야합니다.
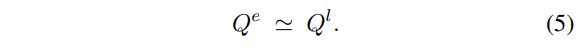
즉, 수식 5가 event와 intensity image간의 관계를 이어줍니다. 위의 수식에서 \epsilon_k, \mathbf{v} 2 가지 변수를 가지고 있습니다. 여기서 \epsilon_k 는 이벤트 카메라의 파라미터로 흔히 상수값으로 사용됩니다. 그렇기에 최종적으로 \mathbf{v} 만 구한다면 두 모달리티에 대한 관계성을 계산할 수 있게됩니다.
Joint contrast maximization
해당 방법론의 베이스가 되는 이전 연구[1]에서는 와핑된 이벤트만을 이용해서 형성된 이미지 (혹은 히스토그램)을 이용하여 flow vector \mathbf{v} 를 최적화하는 contrast maximization (CM)[1]을 제안하였습니다. 그러나 CM은 이벤트만을 고려하여 제안되었습니다. 저자는 CM을 확장하여 intensity image~엣지맵를 함께 활용하여 flow vector를 추정하는 joint contrast maximization (JCM)을 제안합니다.
intensity image~엣지맵과 와핑된 이벤트를 수학적으로 표현하면 다음과 같습니다.
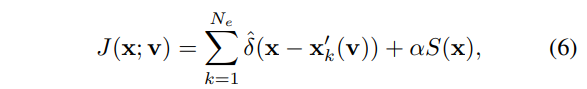
여기서 S()는 엣지맵(e.g. Sobel edge)에 해당하며 \alpha = \frac{N_e}{\sum_{i,j}S(i,j)} 은 이벤트와 엣지맵간의 밸런스를 맞추기 위한 정규화 계수에 해당합니다.
수식 6을 토대로 flow vector에 대한 목적 함수를 정의 하자면 아래 수식과 같습니다.
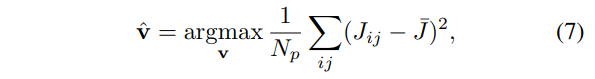
where N_p 는 픽셀의 갯수이며, \bar{J} 는 J에 대한 평균값에 해당합니다. 여기서 intensity image가 없거나 블러한 상황에서는 S()가 0에 가깝게 나오기 때문에 CM과 동일한 기능을 하며, S()가 0이 아닌 경우에는 최대 contrast는 intensity images의 엣지를 기반으로 생성됩니다. 즉, 엣지를 기반으로 flow vector를 추정하게 됩니다.
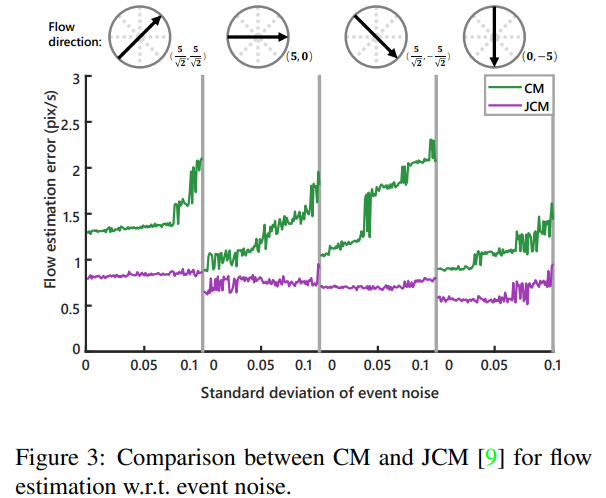
저자는 JCM의 유효성을 증명하기 위해 CM과 JCM를 정량적인 비교 실험 Fig 3을 진행합니다. 해당 실험은 30x30 크기의 이미지 18개의 평균값입니다. 또한 이벤트 노이즈의 강인성을 평가하고자 와 standard deviation range of σe ∈ (0, 0.1)를 따르는 노이즈에서의 평가를 수행합니다. 오차는 5픽셀(radius)에서 유클리디안 거리로 측정된 flow estimation error를 이용합니다. 실험 결과, JCM과 CM 모두 노이즈 정도가 증가함에 따라 에러률도 증가하는 모습을 보이지만, JCM은 CM보다 모든 스펙트럼에서 낮은 오류를 보여주는 걸 볼 수 있습니다.
Joint filtering

해당 섹션에서는 최종적으로 필터링된 값을 얻기 위한 joint/guided filtering을 설명합니다. 이전 섹션에서는 엣지맵과 이벤트 정보간의 연관성을 통해 flow vector를 예측했습니다. 이제 flow vector를 예측했으니, 직접적으로 intensity image와 이벤트의 관계성을 가진 수식 5의 temporal gradient derived Q^e, Q^l 를 구할 수 있게됩니다. 해당 섹션에서는 두 값을 장점을 상호적으로 상속하는 최적화된 출력 Q^o 를 구성하는 것을 목적으로 합니다. output patch Q^o 는 guidance image patch Q^l 의 아핀 변환으로 정의됩니다.
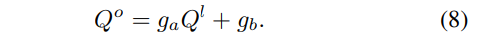
위의 수식을 통해 output patch는 공간적 구조를 상속 받게 되며, 수식 5에 따라 이벤트 정보에 대한 정보도 상속받기 위해 아래의 목적 함수로 정의됩니다.
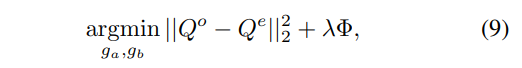
Φ 는 regularization function이며, 유명한 3가지의 emerging filters(Guided Image Filtering;GIF, Side Window Guided Filtering;SW-GF, Mutual-Structure for Joint Filtering;MS-JF)를 사용합니다. 최종적으로 MS-JF을 사용하여 실험에 진행합니다.
+ 여기서 regularization term을 사용하는 이유는 한쪽에 치우치는 현상을 방지하기 위한 장치로, 최종적으로 사용된 MS-JF는 Q^l에서의 아핀 변화 뿐만이 아니라 Q^e에서의 아핀 변화에 대한 상호적인 최적화를 제안하여 두 케이스에 대한 균형을 중시한 최적화 기법입니다.
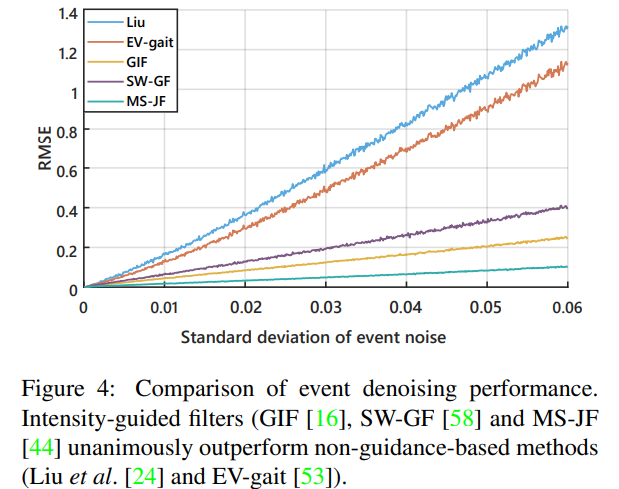
++ MS-JF를 채택한 근거는 Fig 4의 실험적 결과에서 확인할 수 있습니다.
Experiments

실험을 위해서 저자는 이벤트 카메라와 정렬되었으며, 동기화된 프레임 영상이 필요했습니다. 그렇기에 Fig 6과 같은 시스템을 통해 새로운 데이터 셋을 제작하였으며, 리얼 데이터 뿐만이 아니라 이벤트 생성 시뮬레이션을 통해 가상의 데이터를 생성하여 실험을 진행하였습니다.
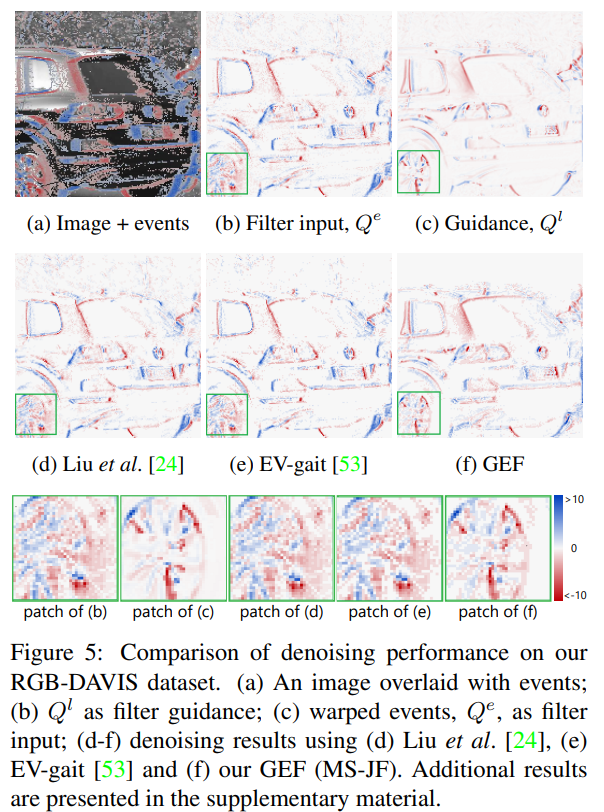
Guided denoising. 가장 먼저, fig 4에서 확인 가능하다시피 제안한 방법이 가장 좋은 결과를 보여줍니다. 또한 정량적인 결과, Fig 5에서도 확인할 수 있다시피 다른 방법론에 비해 이벤트 노이즈가 줄어든 것을 확인할 수 있습니다.
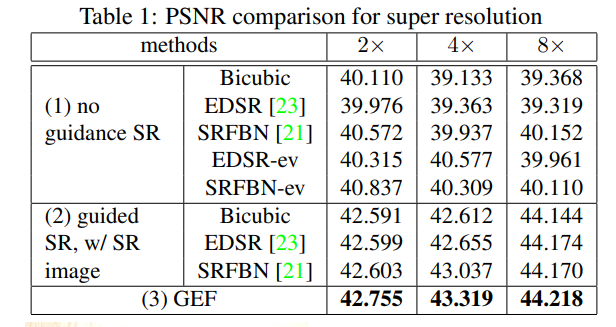
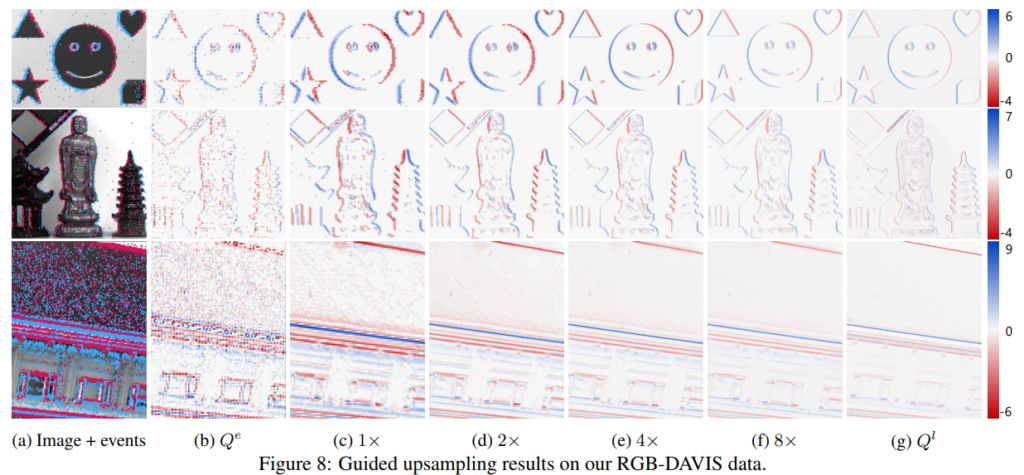
Guided super resolution. Tab 1과 Fig 8에서 SR에 대한 결과를 확인 할 수 있습니다. Tab 1의 @$%-ev는 추가 학습된 결과 입니다. (1)은 Q^l 없이 (2)는 SR과 이벤트간의 joint filtering 수행이 진행된 케이스이며, (3)은 저자가 제안한 방법으로만 수행한 결과 입니다. 최종적으로 제안한 방법에서 가장 좋은 효과를 보여주고 있으며, 해상도에 따른 결과는 Fig 8에서 확인 가능합니다.

Future frame prediction. 12의 프레임에서 예측한 결과, GEF를 사용한 경우에 26.63 (PSNR) and 0.8614 (SSIM)로 개선된 결과를 얻었다고 합니다. 이에 대한 정성적인 결과는 Fig 9에서 확인 가능합니다.

Motion deblur. Fig 10에서와 같이 보다 나아진 결과를 보여줍니다. 디블러링 방법론은 EDI[2]를 사용하여 실험을 진행하였습니다.

HDR image reconstruction. Fig 11을 결과를 보면 Fig 11-(a)의 빛에 과다 노출된 경우에도 불구하고 Fig 11-(b)의 이벤트들이 구조적인 특징을 잘 잡는 모습을 보여줍니다. 그렇기에 Fig 11-(c)에서는 이벤트만을 사용하기 때문에 명암에 영향을 덜 받은 결과를 보여줍니다. 반면에 Fig 11-(d)에서는 intensity image를 함께 사용하기 때문에 명암비가 높아지고 아티팩트가 적어진 특징을 보여줍니다. 해당 실험은 이벤트 기반의 HDR reconstruction[3]을 기반으로 실험을 진행하였습니다.
++ 해당 결과는 intensity의 한계를 보완하다는 주장으로 받아들이면 좋을 듯
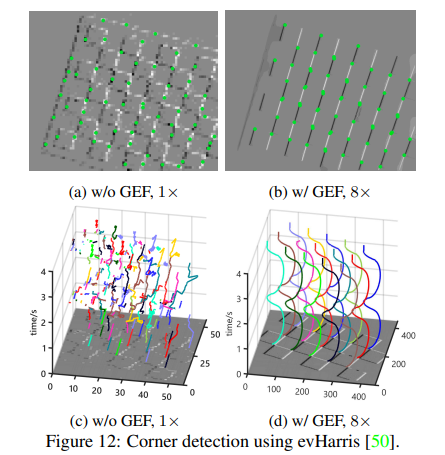
Corner detection and tracking. event-based Harris corner detector (evHarris)를 기반으로 실험을 진행하였으며, fig 6-(b)와 같이 블링크 체크보드(e.g. LCD 화면 속 체크보드)를 이용하여 촬영된 영상으로 진행하였습니다. fig 12에서 보이는 바와 같이 노이즈가 줄어들고 해상도를 높였음에도 좋은 결과를 보여줍니다.
[1] Guillermo Gallego, Henri Rebecq, and Davide Scaramuzza. A unifying contrast maximization framework for event cameras, with applications to motion, depth, and optical flow estimation. In Proc. of Conference on Computer Vision and Pattern Recognition (CVPR), pages 3867–3876, 2018. 2, 3, 4, 5
[2] Liyuan Pan, Cedric Scheerlinck, Xin Yu, Richard Hartley, Miaomiao Liu, and Yuchao Dai. Bringing a blurry frame alive at high frame-rate with an event camera. In Proc. of Conference on Computer Vision and Pattern Recognition (CVPR), 2019. 1, 7, 8
[3] Souptik Barua, Yoshitaka Miyatani, and Ashok Veeraraghavan. Direct face detection and video reconstruction from event cameras. In Proc. of Winter Conference on Applications of Computer Vision (WACV), pages 1–9, 2016. 7, 8
딥러닝이 아닌 논문을 읽는 건 아직 익숙하지 않아서 힘든 것 같습니다. 그래도 근래에 관심이 생긴 이벤트 카메라 기반의 방법론이라 재밌게 읽었습니다. 또한 제가 구성하고자한 시스템을 사용하고 있으며, 노이즈가 발생한 이벤트 영상에 대한 필터링 기법을 제안한 논문이라 주의 깊게 읽었으나... 이해하고 보니 프레임 영상이 정상이며 프레임 영상을 기반으로, 프레임 영상 망가지면 이벤트 기반으로 진행하는 방법론이였네요... 프레임 영상에 대한 의존성이 너무 높기에 좀 아쉬운 논문이였습니다.