이번에 소개드릴 논문은 지난번 튜토리얼 때 설명드린 2번째 논문입니다. CVPR oral paper이며 기존의 transformer랑은 살짝쿵 다른 분야입니다.
Intro
먼저 해당 논문의 인트로는 매우 진부?하게 흘러갑니다. 바로 컨볼루션의 장점 및 단점 그리고 이러한 단점을 해결하기 위한 Self-attention 기반의 vision transformer로의 스토리입니다. 이러한 내용은 저의 transformer backbone 논문 관련 리뷰들을 보시면 알 수 있어서 간략하게만 다루고 넘어가도록 하겠습니다.
Transformer 기반의 방법들은 이미지 패치들을 token으로 보고 해당 token들 사이의 Self-attention 연산을 통해 CNN과 비교하여 상대적으로 넓은 receptive field를 가지고 있습니다. 다만 이러한 연산 과정은 너무나 큰 연산량을 소모하기 때문에 고해상도의 이미지를 처리하는데 있어서는 시간적으로나 메모리적으로나 단점이 크게 존재합니다.
뿐만 아니라 컨볼루션 레이어의 경우 일정한 weight를 가지는 filter가 영상의 전 영역을 주어진 stride만큼 sift하며 연산을 수행하는데 이러한 연산 방식에서 가질 수 있는 locality와 shift invariance 성질 역시 transformer는 가지지 못합니다.
그래서 저자는 이러한 transformer의 연산량은 획기적으로 줄이면서 바로 위에서 언급한 convolution의 성질들 그리고 transformer의 self-attention을 통한 뛰어난 feature 표현력 모두 챙기는 그런 새로운 aggregation layer를 제안한다고 합니다.
Method
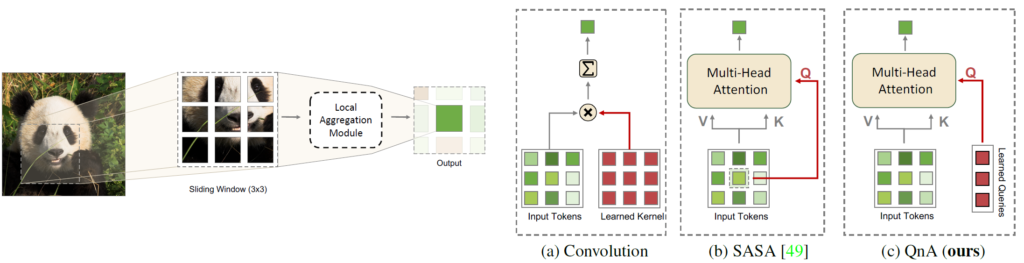
제가 해당 논문의 그림1을 보았을 때 이러한 분야도 있구나 하고 참신해 했었는데 그림1 보시면 어떠한 이미지에 대해서 네트워크가 feature를 생성하기 위한 연산 과정이 나타나있습니다. (a)는 저희가 잘 아는 convolution 연산을 나타내고 있는데, (b)와 (c)가 저는 개인적으로 흥미로웠습니다.
(b)와 (c)는 마치 convolution처럼 주변 이웃 픽셀에 대하여 연산을 수행하는데 실제 연산 과정은 고정된 filter 값과 그 위치에 대응되는 픽셀값이 곱하고 더하는 그런 컨볼루션 연산이 아닌 Self-attention 연산을 수행하는 것입니다. 여기서 헷갈리지 말으셔야 할 것이 영상의 특정 패치 레벨끼리 연산하는 것이 아닌 일정 패치 안에서의 연산을 self-attention으로 한다는 점입니다.
즉 일정한 영역에서 이러한 self-attention을 진행했다면 마치 convolution layer처럼 특정한 stride 값만큼 sift한 다음 그 주변 이웃 픽셀들끼리 다시 또 self-attention 연산을 수행하는 그런 것이죠.
이를 한번 수식적으로 정리해보겠습니다. 일단 일반적인 컨볼루션 연산은 아래 수식처럼 나타낼 수 있습니다.
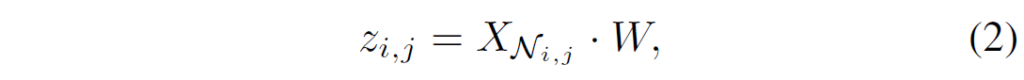
여기서 X는 input feature( R^{H \times W \times D}), W는 kernel(R^{k \times k \times D \times D}를 의미합니다. 그리고 Self-attention은 아래 수식처럼 나타낼 수 있습니다.
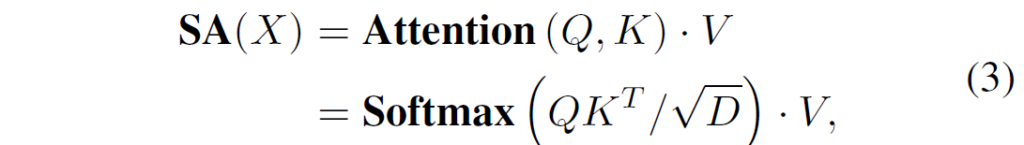
여기서 Q와 K, V는 Query, Key, Value token을 의미하며 실제 Attention 연산은 Q와 K에 대하여 dot product를 한 후 token의 길이(D)만큼 나누어 Softmax 연산을 수행합니다. 그렇게 만들어진 attention map을 Value token에 또 dot product를 진행함으로써 실제로 중요하게 볼 부분과 그렇지 않은 부분을 지정해주는 것입니다.
Query-and-Attend
자 그럼 이제 본격적으로 convolution 연산을 대체한 SASA라는 방법론과 제안하는 QnA 논문을 살펴보도록 하겠습니다. 먼저 SASA과 QnA 방법론은 각 이웃 픽셀들끼리의 self-attention 연산을 하는 것이라고 말씀드렸습니다. 여기서 SASA는 2019년도 NeurIPS에 나온 논문으로 QnA 논문과 비교대상으로 볼 수 있는데 SASA는 이웃 9개의 픽셀들을 key와 value로 보고 9개 중 정 가운데 셀을 query token으로 놓고 계산하게 됩니다.
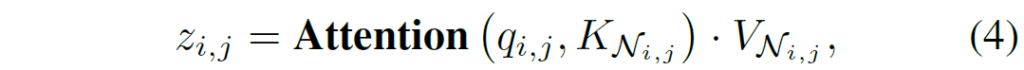
여기서 q_{i,j} = X_{i, j}W_{Q} 입니다. 여기서 K와 V는 K_{i, j}가 아닌 K_{N_{i, j}} 인 것을 보면 아시다시피 위 설명처럼 주변 9개의 셀에 대한 K와 V라고 보시면 됩니다.
저자는 이러한 SASA가 표현력이 뛰어나고 convolution의 locality 특성을 잘 담았기는 하지만 문제는 연산량 및 메모리 사용량이 너무 크다고 주장합니다. 이에 대한 원인으로는 9개의 주변 셀 중 정중앙부가 query로 사용되고 해당 query에 key와 value 집합에 attention 연산을 취해주기 위하여 unfolding이라는 함수를 사용한다고 합니다.
하지만 이러한 unfolding 작업은 연산량이 너무나도 많이 들기 때문에 실제 고해상도 이미지에 대하여 올바른 처리를 못한다고 하네요.
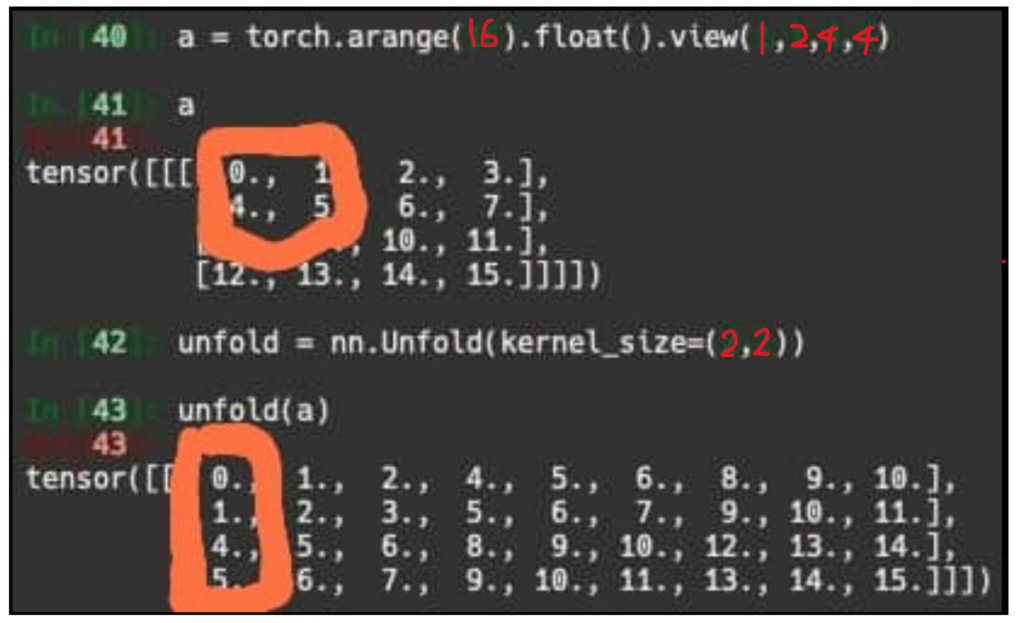
unfolding이라는 함수에 대해 저도 해당 논문을 통해 처음 접하는 것이라 모르시는 분들을 위해 설명을 드리자면, 일반적인 reshape과 달리 unfold 함수는 일종의 컨볼루션 연산을 벡터로 수행하기 위한 전처리 과정이라고 이해하시면 됩니다.
이게 무슨 말이냐면 위의 예시에서 41번째 라인에서의 변수 a는 2×2 patch에 대하여 0,1,4,5로 구성되어있습니다. 이 때 2×2 컨볼루션 커널에 대하여 연산을 수행하게 되면 주황색 박스를 친 0,1,4,5 부분이 처음 연산을 수행하게 되는데 이러한 행렬의 연산 과정을 벡터의 곱셈으로 표현하면 1×4 kernel weight와 [0,1,4,5]^T로 나타낼 수 있습니다.
요약하자면 unfold는 행렬과 유사한 방식으로 연산하는 과정을 벡터 연산으로 수행하기 위해 표현을 바꾸는 함수라고 보시면 될 것 같으며 이러한 unfold 과정이 위에 말한 SASA 방법론 구현에 들어가게 됩니다.
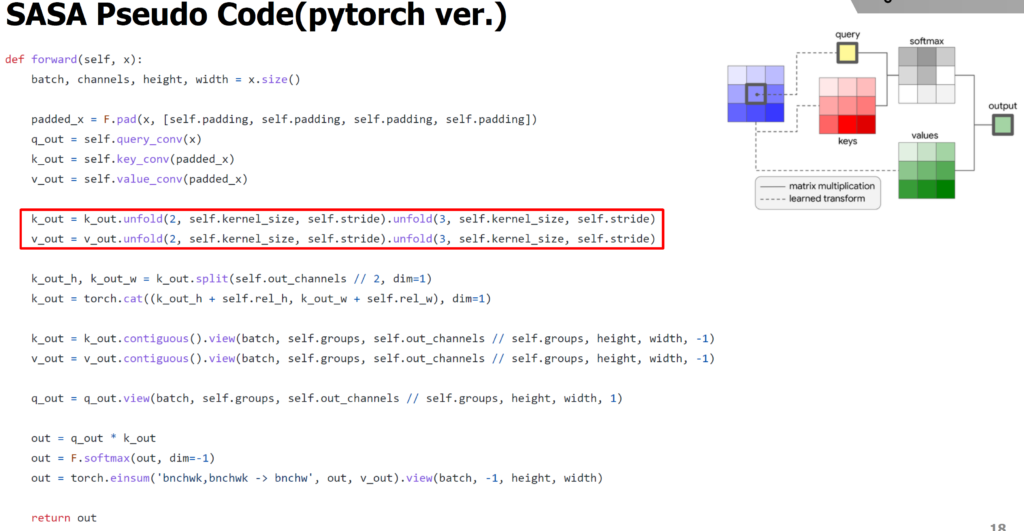
반면에 논문에서 제안하는 QnA의 경우에는 Query를 중앙에서 추출하는 것이 아닌 학습 가능한 파라미터(weight)를 가지고 attention 연산을 진행하게 됩니다. 즉 key와 value는 token 형식으로 지니고 있는 반면에 query는 학습 가능한 파라미터로 보게 되는 것입니다.
저자는 이러한 연산 과정을 key의 벡터가 query의 weight에 곱해짐으로써 query imebedding space로 투영된다고 말합니다. 이렇게 투영된 key vector 중 값이 큰 것들은 query와 유사도가 높은 것이며 값이 작으면 query와의 중요도가 떨어진다 라고 보면 된다 합니다.
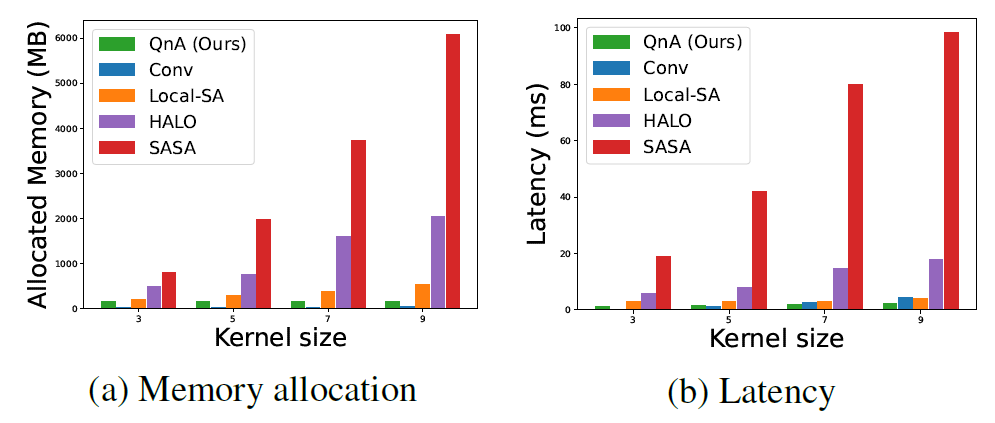
결론적으로 학습 가능한 query를 통해 Key와 value에 대한 attention 연산을 수행하기 때문에 결과적으로 자신들이 제안하는 방법은 unfold 함수를 사용하지 않아도 되며 이는 메모리 측면에서 큰 이점을 본다고 주장합니다.
Experiments
저는 알고 있으니 넘어갈게요^^ 자 그러면 실험 섹션에 대해서 간략하게 다루고 마무리 짓도록 하겠습니다.
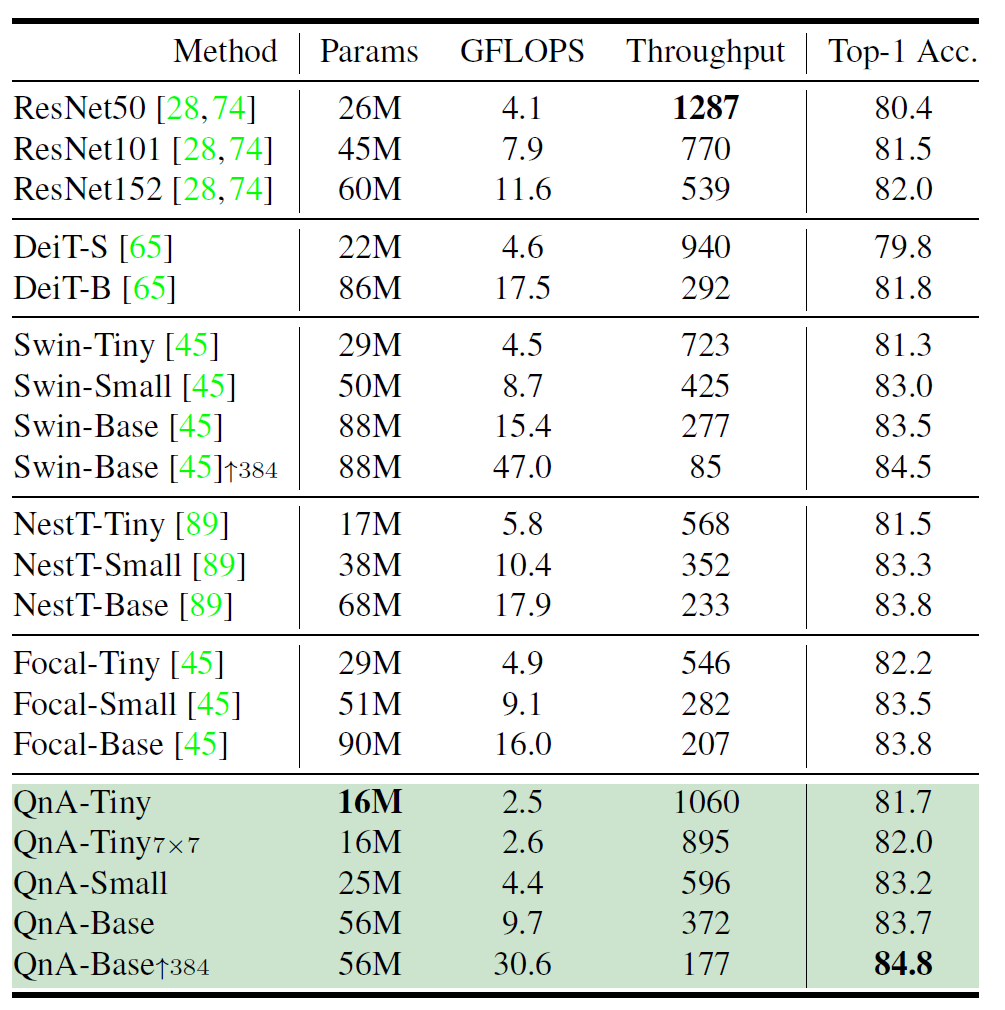
먼저 위의 표는 ImageNet-1K에 대한 분류 결과로 제안하는 방법론이 타 방법론과 비교하였을 때 성능이 비슷하거나 더 좋은 것을 확인하실 수 있습니다. 예시로 Base 네트워크 규모로 비교하였을 때 QnA-B는 Focal-B보다는 성능이 0.1 더 낮지만 학습 파라미터와 Throughput을 비교하였을 때는 훨씬 큰 폭으로 더 가볍고 빠른 것을 확인하실 수 있습니다.
이러한 경향성은 Base 뿐만 아니라 Small, Tiny에서도 동일하게 나타납니다. 즉 해당 논문은 성능은 기존의 Sota에서 유지한 채로 모델의 경량화에 큰 기여를 했다라고 보시면 될 것 같습니다.
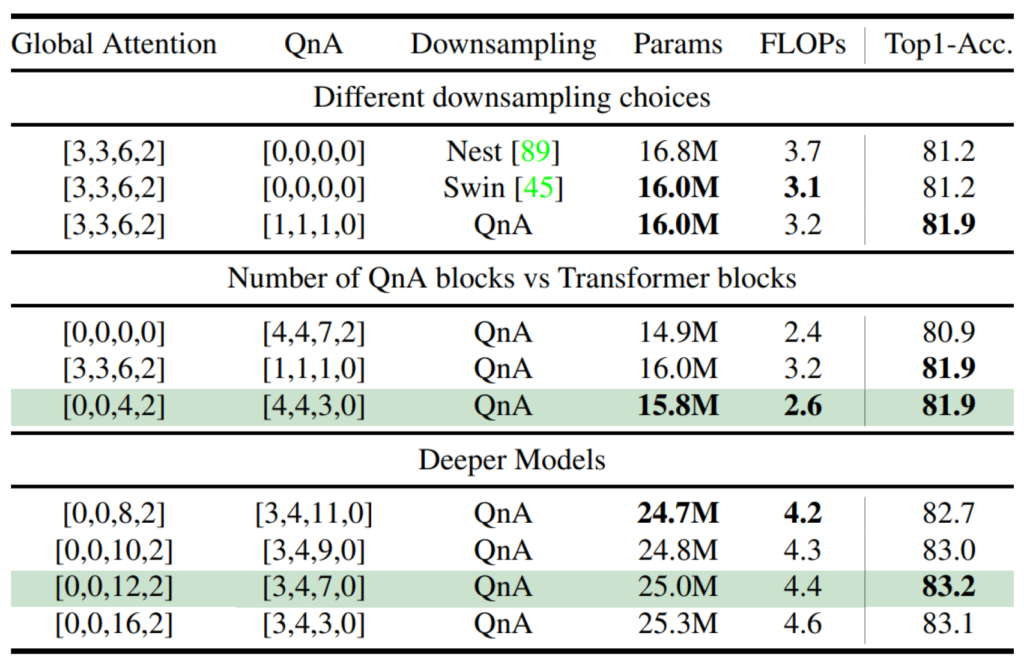
다음은 Ablation study에 대한 결과인데 위에서부터 차례로 downsampling layer를 무엇을 사용할지와 QnA block과 Transformer block의 적절한 조합 그리고 더 깊은 레이어에서의 조합 결과를 보인 것으로 이해하시면 됩니다.
먼저 downsampling의 경우 제가 계속해서 말씀드렸다시피 QnA 방법론은 결국 컨볼루션 레이어의 역할을 그대로 모방하기 때문에 컨볼루션이 할 수 있는 연산이라면 QnA도 모두 동일하게 진행할 수 있습니다.
그 중에서 가장 흔한 것이 바로 upsampling과 downsampling이 있는데 일반적으로 3×3 커널사이즈의 2 stride 값을 가지면 down-sampling이 되는 것처럼 QnA도 stride 값을 잘 조절하면 down-sampling을 진행할 수 있게 되는 것이죠. 저자는 이러한 관점에서 자신들이 제안하는 QnA down sampling 방식과 기존의 Swin, Nest backbone이 사용한 down-sampling 방식을 비교하는 결과를 맨 위의 표에서 보입니다.
Swin과 Nest는 쉽게 말해 흔히들 사용하는 3×3 또는 2×2 컨볼루션과 stride로 down-sampling하는 과정을 의미합니다. 놀라운 점은 논문에서 제안한 QnA 기법으로 down-sampling을 하였을 때 모델의 파라미터는 Swin down-sampling과 동일하면서 정확도가 무려 0.7% 상승했다는 점입니다.
그리고 중간과 맨 아래 표에서는 이제 QnA와 Transformer block 즉 저희가 흔히 아는 feature의 patch level 별로 global하게 self-attention 수행하는 block의 조합을 취했을 시 어떤 것이 성능이 좋은가에 대한 결과인데, 보시면 Self-attention 연산을 3~4스테이지에서 다루는 것이 좋고 QnA는 앞 스테이지 위주로 진행하는 것이 성능과 속도 측면에서 가장 효율적이었다고 합니다.
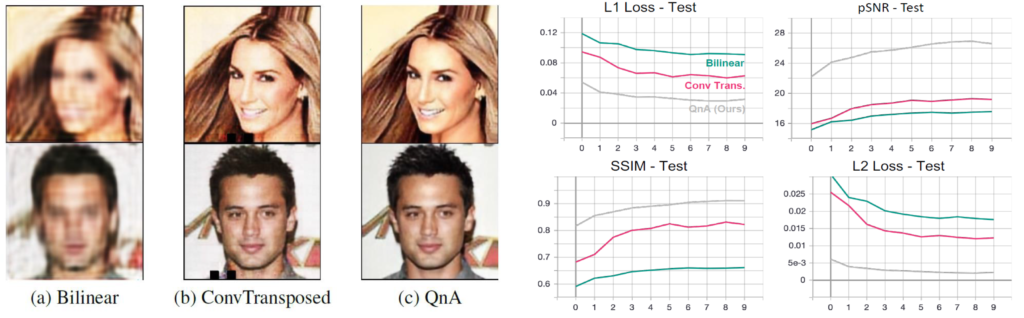
다음으로는 제가 가장 흥미롭게 봤던 실험 부분으로 위에서 설명한 down-sampling 뿐만 아니라 upsampling을 수행할 때의 QnA 유효성을 검증한 부분입니다. 저자는 QnA upsampling의 성능을 보기 위해 5개의 layer로 구성된 encoder-decoder 구조 네트워크로 영상 합성 task를 진행하였습니다.
encoder는 5개의 down-sampling layer로 구성되어있으며 decoder 역시 5개의 upsampling layer로 구성되는데 이 때 upsampling layer의 효과만을 제대로 비교하기 위하여 encoder는 모두 동일한 구조를 활용하였고 디코더 부분만 흔히들 많이 사용하는 bilinear interolation& converolution 조합, ConvTransposed layer, 그리고 제안하는 QnA upsampling layer를 통해 실험을 진행하였다고 합니다.
그 결과는 바로 위 그림에서 확인하실 수 있는데 가장 먼저 좌측에 정성적 결과를 살펴보시면 (a)는 전혀 무엇인지 모르겠는 마치 블러한 이미지처럼 생성이 되었으며 (b)의 경우 얼핏 보았을 때 잘 만든 것처럼 보이지만 중간중간에 hole이 생기거나 선명하지 못한 현상이 발생합니다.
반면 QnA의 경우에는 마치 GAN 방법론으로 학습시킨 것처럼 상당히 선명하고 자연스러운 결과를 나타내는 것을 확인하실 수 있습니다.(참고로 학습 과정에서는 GAN loss가 아닌 L1 loss만을 사용하였다고 합니다.)
실제 우측의 정량적 결과에서도 L1, PSNR, L2, SSIM 4가지 지표로 평가를 수행하였는데, 여기서 SSIM만을 설명드리자면 QnA로 학습한 방법이 SSIM 수치가 0.9를 넘고 있습니다. SSIM 값이 0~1의 값을 가지는데 1에 가까울수록 원본과 동일하다고 보시면 되며 제가 실제로 SSIM 관련 수치로 영상 변환 분야에서 평가해보았을 때 0.9라는 수치면 거의 원본과 동일하다고 보셔도 무방할 정도의 수치임을 나타냅니다.
결론
저는 그냥 일반적인 transformer backbone 논문인 줄 알았는데 알고보니 컨볼루션 레이어와 유사하지만 컨볼루션 연산을 대체하는 그런 종류의 방법론이라서 일차로 놀랐고, 그리고 실제 단순히 feature aggregation 뿐만 아니라 upsampling, down-sampling에서도 큰 향상을 보인다는 것에서 매우 흥미롭게 봤던 논문입니다.
물론 중간에 unfold 과정에서 이해가 가지 않는 부분들도 존재를 하긴 했으나, 결과적으로는 unfold라는 함수를 사용하지 않은 구조를 제안한 것이니깐 그것 나름대로 긍정적이라고 생각합니다. 아쉽게도 코드는 pytorch가 아닌 jax-Flax?라는 라이브러리로 구현된 것 같아 조금 아쉽지만 파이토치랑 유사한 틀인 것 같아서 필요하신 분들은 어렵지 않게 포팅할 수 있을 듯 합니다.