Abstract

최근 deeplearning 기반의 방법론을 이용하는 방식이 전통적인 기법을 크게 능가하고있다. 그러나 기존의 ranking-tailored loss 함수를 이용하는 방식은 mAP를 최적화하는 방식이 아니라는 이론적 한계와, 상당한 engineering 과정이 요구된다는 실용적 측면에서 한계가 있었다. 이에 대응하기 위해, 해당 논문은 발전된 listwise loss formulation을 이용하여 직접 global mAP를 최적화하는 것을 제안한다. AP를 미분가능하게 만들어 end-to-end로 학습할 수 있으며, 동시에 수천장의 이미지를 고려할 수 있고 트릭을 사용하지 않아도 된다는 장점이 있다. 또한 많은 이미지 retrieval 벤치마크에서 SOTA를 달성하였다.

Introduction

ranking 기반의 loss함수들은 2,3,…,n쌍의 이미지에 대하여 고려하였고 이들의 공통 원리는 작은 이미지 set을 sub sampling하고, 이미지들이 local하게 ranking이 되었는지 확인하고, 아닐 경우 모델 업데이트를 하는 과정을 반복하는 것이다. 그러나 이러한 ranking 기반의 loss는 loss의 상한을 줄이는 방식으로 mAP를 최적화하도록 학습된다는 보장이 없다.(이론적 측면에서의 한계) 따라서 사전학습, multiple loss의 결합, 복잡한 hard-negative mining방식과 같이 많은 engineering 과정이 요구된다.(실용적 측면에서의 한계)

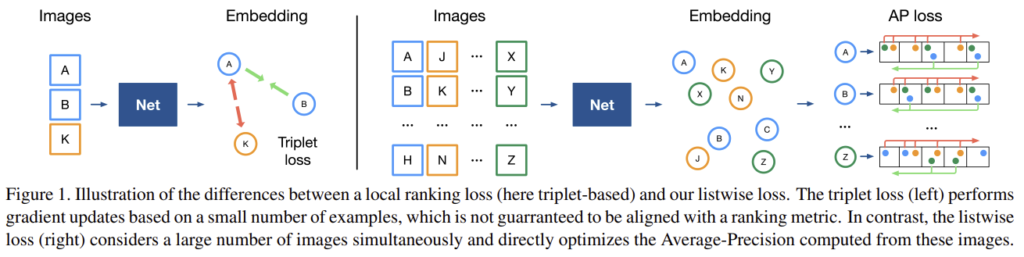
이러한 이유로 해당 논무은 mAP를 직접 최적화할 수 있도록 새로운 loss를 제안한다. 그림1과같이 한번에 2개가 아닌 수천장의 이미지를 고려하여 global한 순위를 동시에 최적화한다. 이를 통해 추가적인 engineering 과정을 불필요하게 만든다. 이때 AP는 일반적으로 smooth하지 않고 미분이 불가능하여 gradient 기반의 프레임워크에서 직접적으로 최적화를 할 수 없었으나 histogram bining(soft bining)을 이용함으로써 AP에서 미분 불가능한 sorting 작업을 대체하여 딥러닝이 가능하다.

Method

1. Definitions

(이후의 method에 나오는 수식에 대한 이해를 위해 문제를 수식적으로 정의한 부분입니다.)

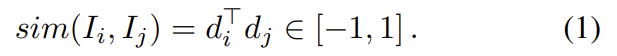
query image I_q에 대하여 N크기의 데이터베이스 안의 이미지 \left\{ I_i \right\}_{1≤i≤N}들간의 유사도를 (1)의 식을 이용하여 sim(I_q,I_i)=S_i^q 구한다. 이후 내림차순으로 데이터를 정렬한다.

ranking함수를 R:\mathbb{R}^N ×\mathcal{N}→\mathcal{N} (\mathcal{N}=\left\{1,2,…,N\right\} )로 정의하였을 때 R(S^q,i)는 S^q의 i번째로 높은 값의 인덱스를 의미한다. R(S^q)는 데이터베이스의 ranked 인덱스 리스트를 의미한다. R(S^q)는 GT값인 Y^q와 각각 관련성을(\left\{0,1\right\}^N) 이용하여 평가한다. Y^q_i는 I_i와 I_q가 관려있으면 1, 아니면 0이 된다. AP는 다음 식을 이용하여 구할 수 있다.

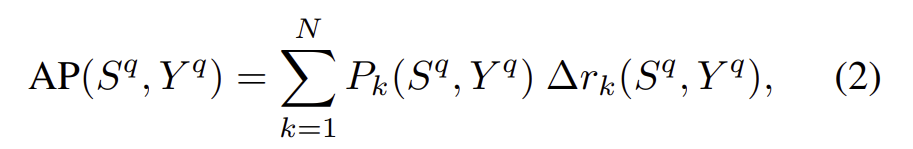
이때 P_k는 k 랭킹의 정확도로 k의 첫번째 인덱스에 있는 관련 아이템의 비율이다.

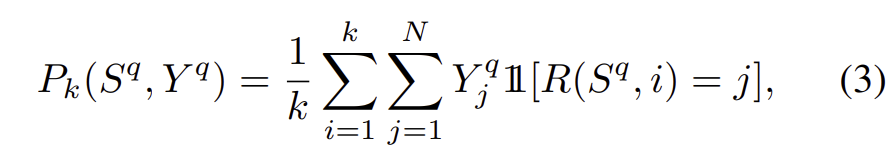
∆r_k는 k rank에서 발견된 관련 아이템의 전체 개수N^q=\sum^N_{i=1}Y^q_i의 비율이다.

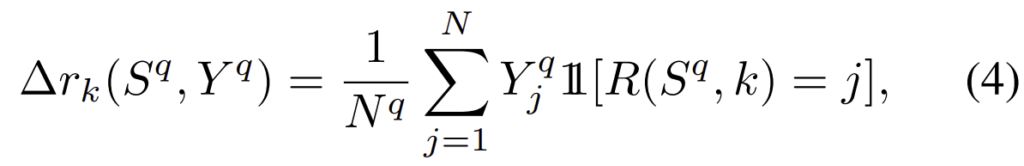
은 지시함수로 집합에 특정 값이 속하면 1, 아니면 0이 되는 값을 갖는 함수이다.

2. Learning with average precision

(수학적인 내용으로, 아래의 다시 정리한 부분을 참고하세요)

모델이 AP가 최대가 되도록 학습해야 하지만 지시함수가 있으면 학습을 할 수 없다. 따라서 지시함수를 back-propagation이 가능한 \delta함수로 대체하여 학습한다. 이 함수는 유사도값을 고정된 bin으로 soft-assign한다.

Quantization function

모든 순위 k에서 precision과 recall을 구한다.

\left\{b_m\right\}_{1≤m≤M}은 bin의 중심값으로, b_m=1-(m-1)∆ (이때 ∆={{2}\over{M-1}})일때 간격 \bar{b}_m는 \bar{b}_m = [max(b_m - ∆,-1),min(b_m + ∆,1)]이다.

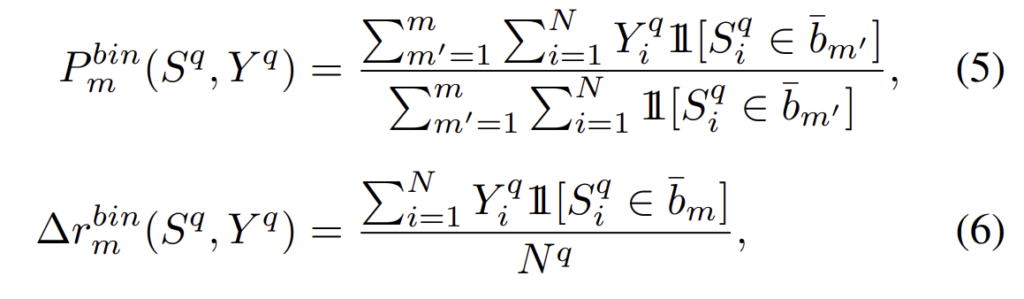
다음으로 indicator를 대체하기 위해 soft-assignment를 이용하는 단계로 이때 \delta (·,m)는 b_m주변에 너비가 2∆가 되도록 \delta:\mathbb{R}×\left\{1,2,...,M\right\}→[0,1]정의한다.

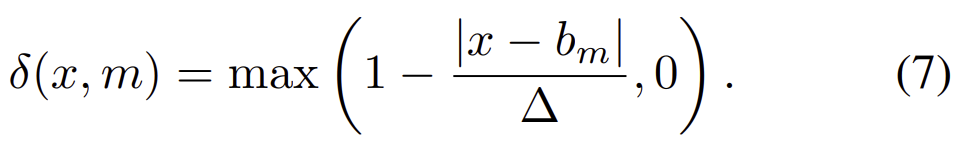
각 bin m에 대하여 quantized precision \hat{P}_m와 증분의 recall ∆\hat{r}_m은 다음과 같이 계산이 된다.

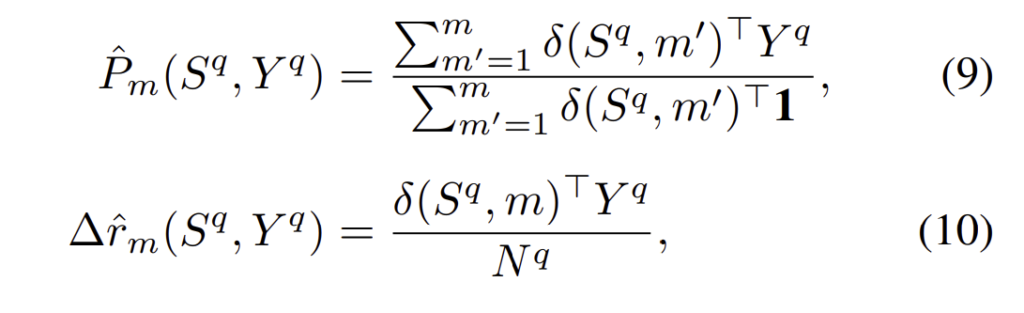
결과적으로 quantized average precision AP_Q를 얻는다.

---

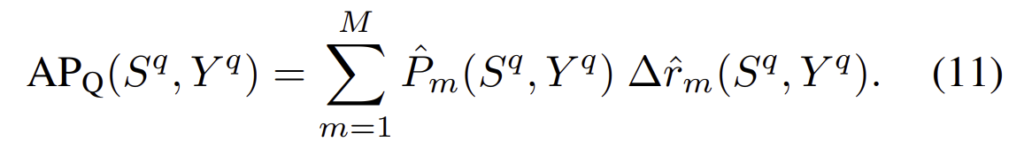
위의 내용은 수식적으로 풀이한 내용이고, 이해를 위해 다시 정리하였다.

[-1,1]구간을 등간격을 갖는 M-1개로 나누어 M개의 bin center \left\{b_m\right\}_{1≤m≤M}를 생성한다. 이때 bin center b_m 은 bin을 중심으로 양 옆에 ∆만큼의 너비를 가지게 된다.

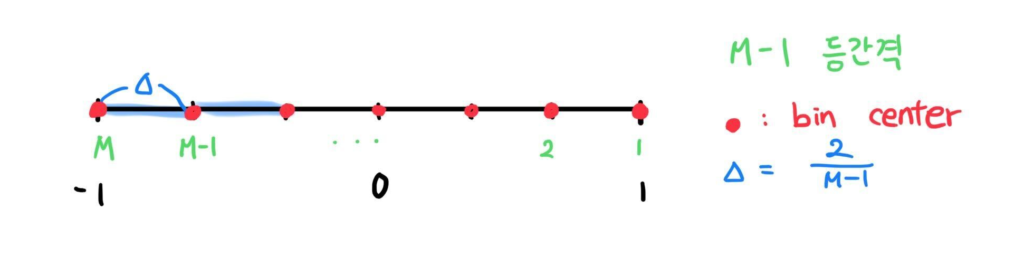
이후 함수를 대체하기 위해 \delta함수를 사용한다. 이를 통해 학습이 가능해진다. 식(7)이 \delta와 관련된 부분으로, |x-b_m|이 ∆보다 크면, b_m에 해당하지 않는 값이므로 0의 값이 되고, |x-b_m|이 ∆보다 작으면, b_m에 할당되어야 하는 값으로 0이 아닌 값을 갖게 된다. \delta함수를 통해 smooth하고 미분 가능하도록 만든 것이다.

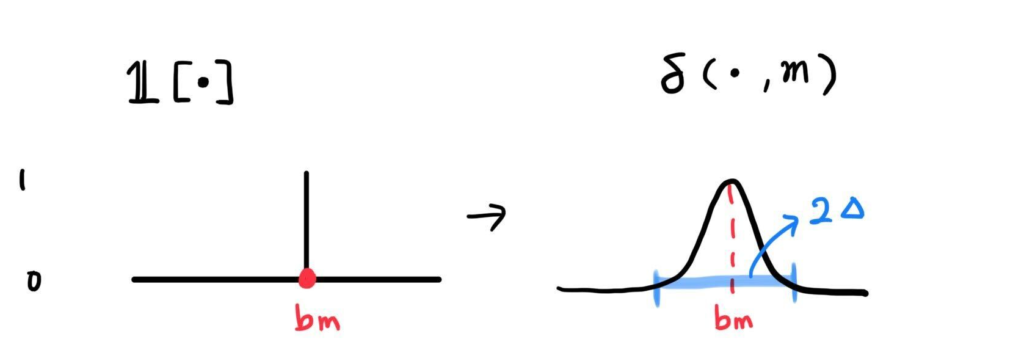
이를 기반으로 식(9)와(10)을 계산하고 AP_Q(식(11))를 구한다.

---

Training procedure

배치사이즈가 B라 할 때, 학습은 배치에 대한 mAP_Q를 계산한다. 이때 각 배치에 해당하는 이미지들은 모두 잠재적 query가 되어, 배치의 다른 이미지들과 비교하여 유사도를 계산하고 precision과 recall을 구한다. mAP식은 다음과 같고,

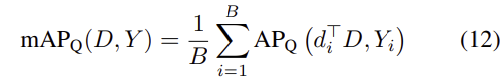
i가 배치내의 이미지, Y_i는 이미지 i에 대해 다른 이미지들과 비교한 GT로 동일한 label일 경우 1, 아닐 경우 0의값을 갖는다. D는 배치에 해당하는 descriptor들 d_b(1,2,...,b,...,B)의 모음이다.

loss는 다음 식으로 정의된다.

Training for high-resolution image

높은 해상도의 이미지를, 큰 배치사이즈로 학습을 하는 경우 더 좋은 성능을 얻을 수 있지만, 용량의 문제로 어려움이 있었다. 이를 해결하기 위해 chain rule을 이용하여 multistaged backpropagation을 디자인하였고 메모리 문제를 해결하였다. 아래의 그림2에 방식이다.

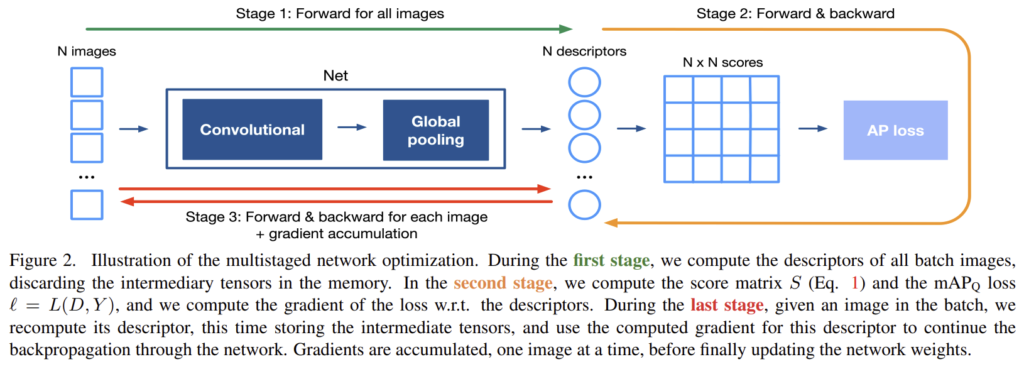
1. 배치의 모든 이미지의 descriptor 계산
2. 식(1)을 이용하여 score matrix S 계산하고 loss=L(D,Y)를 이용하여 descriptor에 대한 loss의 gradient 계산
3. 이미지별로 descriptor 다시 계산하고 중간 tensor 저장

정리하자면 evaluation 과정처럼 네트워크와 수식을 통해 descriptor와 score matrix를 구한뒤, 이미지를 하나씩 이용하여 gradient를 구하고, 한번에 업데이트를 진행한다.

Experimental results

Datasets

• Landmarks
  original dataset은 검색엔진을 이용하여 반자동 방식으로 구해진 것으로, 잘못된 라벨이 많았고, 이를 처리한 Landmarks-clean 데이터셋을 이용하였다. 42410장의 이미지와 586개의 landmark가 있고 학습에 사용한다.
• Oxford and Paris Revisited
  Revisited Oxford(\mathcal{R}Oxford)와 Revisited Paris(\mathcal{R}Paris)는 각각 4933장, 6322장의 이미지를 가지고 있고 각각 70장의 query로 이용되는 추가 데이터가 있다. 라벨은 구별하기 어려운지에 대하여 easy,medium,hard 3가지의 추가 레이블이 있다.

Parameter study

• Batch size
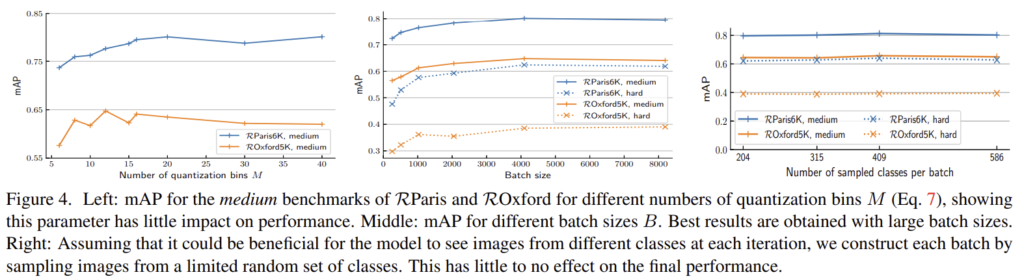
  배치가 클수록 좋은 성능이 나옴을 확인하였다.(그림(4) 가운데 참고) B=4096에서 성능이 saturation되고 속도도 느려지므로 B=4096으로 설정하였다.
• Class sampling
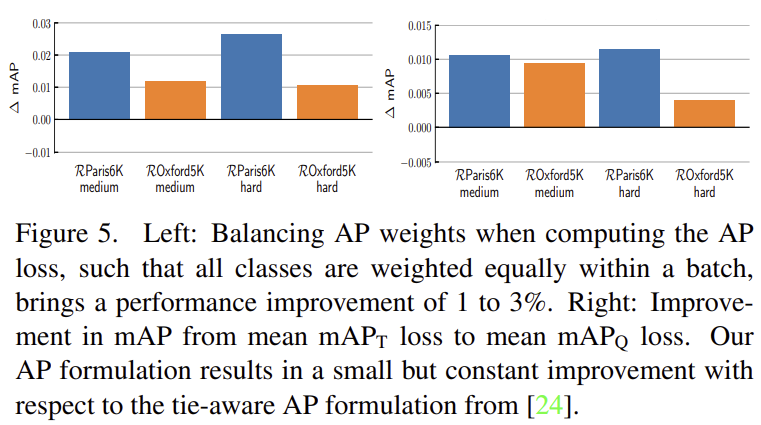
  class imbalance 문제를 해결하기 위해 식(12)에 가중치를 도입하였고 그 결과 약 2%의 성능 향상을 확인할 수 있다.(그림5)
• Tie-aware AP
  [Kun He. etc. Hashing as tie-aware learning to rank.]에서 제안된 tie-aware version을 이용하여 mAP_T로 표시된 단순화된 tie-aware AP mAP_T를 이용할 때와 성능 차이를 확인하였고 그림5에서 확인할 수 있다.
• Score quantization
  bin을 구성하는 M에 따른 성능 변화를 확인하였고 그림4(왼쪽)에서 확인할 수 있다. M=20으로 설정하였다.
• Descriptor whitening
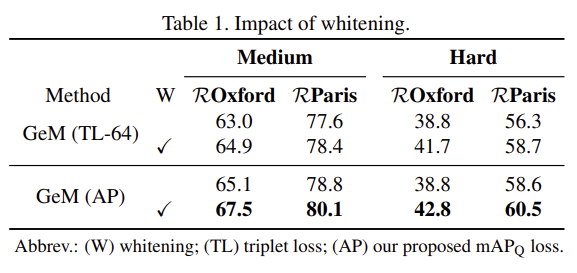
  descriptor에 whitening의 효과를 확인해보았고 성능 향상을 확인하여 이후에 whitening을 계속 적용하였다. (Table1 참고)
  

Ceteris paribus analysis

제안한 loss를 이용하였을 때의 장점에 대해 분석하였다. 이를 위해 다른 과정은 그대로 두고, loss를 hard-negative mining을 사용하는 triple loss(TL)로 바꾸었다. (TL 뒤의 숫자는 배치사이즈를 의미한다.)

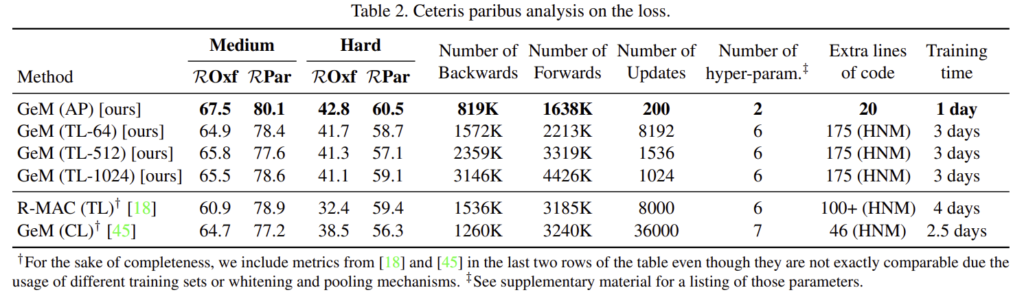
hard-negative-mining을 적용하지 않았음에도 mAP_Q loss를 이용하는것 만으로도 3% 가량의 성능 향상을 확인할 수 있었다. 또한, TL을 이용할 경우 배치사이즈가 커져도(업데이트 전에 더 많은 데이터를 고려하더라도) 성능 향상이 일어나지 않는 다는 것을 확인할 수 있었고, 이는 mAP_Q loss를 이용하는 것이 단순히 큰 배치사이즈를 이용하기 때문에 얻을 수 있는 장점이 아님을 보여준다.

추가로 표2를 통해 backward 횟수, 업데이트 수 등 다양한 요소를 고려할 때 제안한 학습방식이 효과적임을 알 수 있고, 훨씬 적은 파라미터가 요구되는 것을 알 수 있다.

Comparison with the state of the art

SOTA 방식들과의 성능 비교로, CL은 contrastive loss, TL은 triplet loss, AP는 이 논문에서 제안한 mAP_Q loss를 이용한 경우, O는 loss를 이용하지 않은 경우를 의미한다.

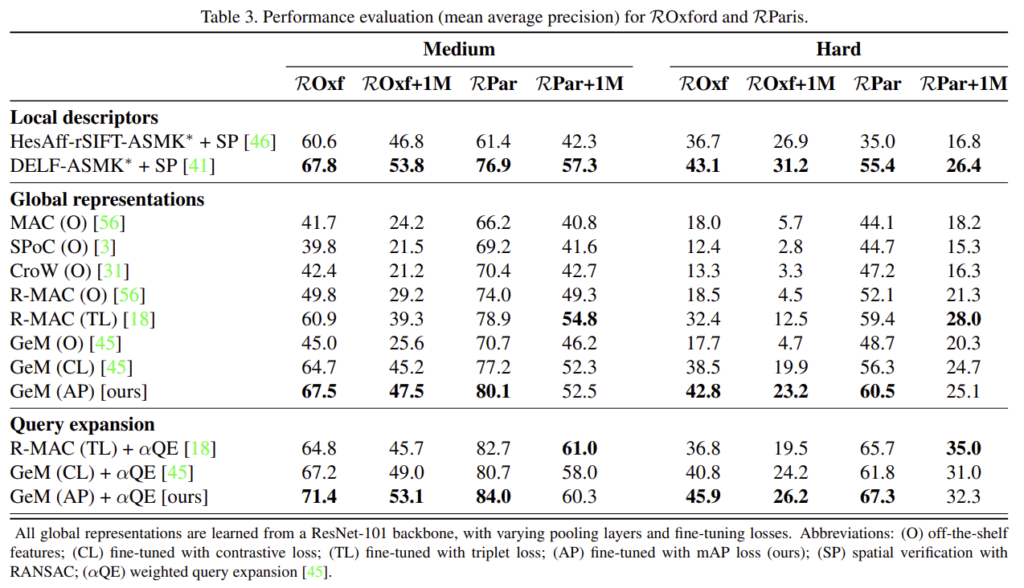
전반적으로 SOTA방법론들과 비교했을 때 1~5%성능이 향상되었다. 제안한 방법론은 사전학습 단계를 필요로하지 않으므로 시간도 단축할 수 있다.

** 해당 방법론은 global descriptor에 의존하므로 기하학적 검증은 부족하다.