1. Abstract

2개의 local feature의 대응되는 것을 찾고, 맞지않는 포인트는 거부하여 matching하는 SuperGlue라는 neural network를 소개한다. attention 기반의 super glue가 3D 장면 이해와 feature assignment를 공동으로 추론할 수 있도록 하는 융통성있는 context aggregatoin 방식을 소개한다. end-to-end로 학습을 통해 기하학적 변환과 3D 세계에서의 규칙을 우선적으로 학습한다. 실제의 실내와 실외 환경에서 pose를 예측하는 챌린지에서 SOTA를 달성하였으며, SLAM과 SfM에 쉽게 합쳐질 수 있다.

2. Introduction

3D 구조와 카메라의 포즈를 예측해야하는 컴퓨터비전 task에서 대응점 매칭은 필수적이다. 이 논문에서는 기존에 존재하는 local feature matching 과정을 SuperGlue를 이용하여 학습할 것을 제안한다.

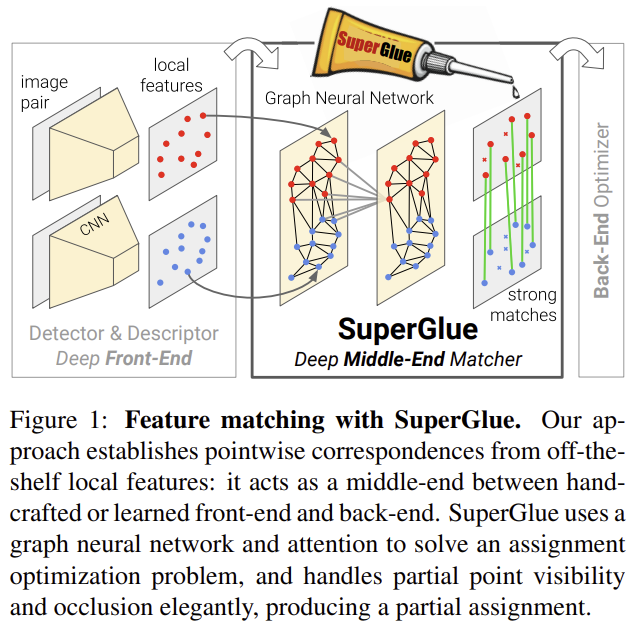
feature matching을 두 이미지간의 특정 위치 찾는 것으로 본다. graph-based 전략을 이용하여 linear assignment 문제로 해결한다. 최적화의 비용함수는 GraphNeural Networ를 이용하여 예측된다. keypoint와 시각적 외관을 모두 활용하기 위해 self-(intra image)/ cross-(inter image) attention을 이용한다. 이는 예측의 할당 구조를 강제하고, 복잡한 사전학습, occlusion과 non-repeatable keypoint를 다룰 수 있게 해준다. 또한 end-to-end로 학습이 가능하며, multiple-view geometry 문제에 적용이 가능하다.(그림2 참고)

3. The SuperGlue Architecture

Motivation

image matching 문제는 규칙을 이용하여 문제를 해결할 수 있다.

• 3D world는 대체로 smooth하며, 때로는 평면적이다.
• static한 장면에서 대응점은 epipolar 변환을 이용하여 구할 수 있다.
• 2D keypoint는 두드러진 3D 포인트를 투영시킨 것으로 이미지간의 대응점은 다음의 제약조건을 가진다.
  1. 다른 이미지에서 최대 1개의 대응되는 점을 가질 수 있다.
  2. occlusion이나 detector의 fail로 인해 일부는 매칭되는 지점이 없다.

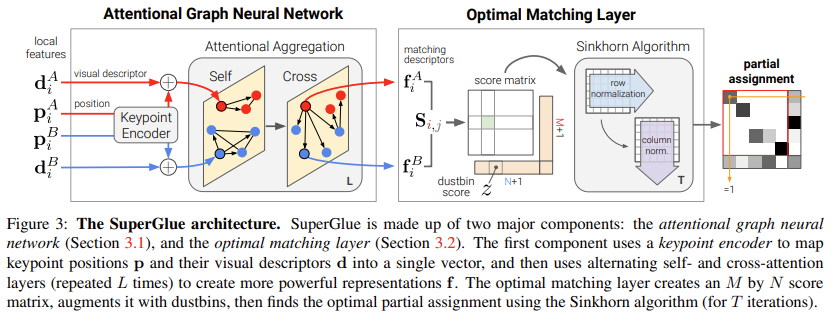
Formulation

두 이미지 A와 B에 대하여 local feature는 keypoint의 위치 \mathbf{p}와 descriptor \mathbf{d}를 함께 (\mathbf{p},\mathbf{d})로 나타낸다. 이때 \mathbf{p}_i = (x,y,c)_i로 x,y는 좌표, c는 detector의 confidence를 나타낸다. \mathbf{d}_i 는 SuperPoint과 같은 CNN 방식이나 SIFT와같은 전통적인 방식으로 뽑을 수 있다. (SuperGlue의 task는 point의 matching에 있음!)

Partial assignment

\mathbf{P}는 두 이미지 A,B의 piont들에 대한 신뢰도 map으로 0~1의 값을 가지게 된다.

3.1. Attentional Graph Neural Network

keypoint의 위치 정보와 시각적 외관 정보 외에도 contextual한 단서를 활용하면 직관적으로 구분력을 높일 수 있을 것이다. 사람의 경우도 이미지에서 keypoint를 찾으라 하면 두 이미지의 잠정적인 keypoint를 찾은 후 각각을 평ㅇ가하고, 맥락정보를 활용한다. 이러한 방식을 통해 Attentional Graph Neural Network을 디자인하였다.

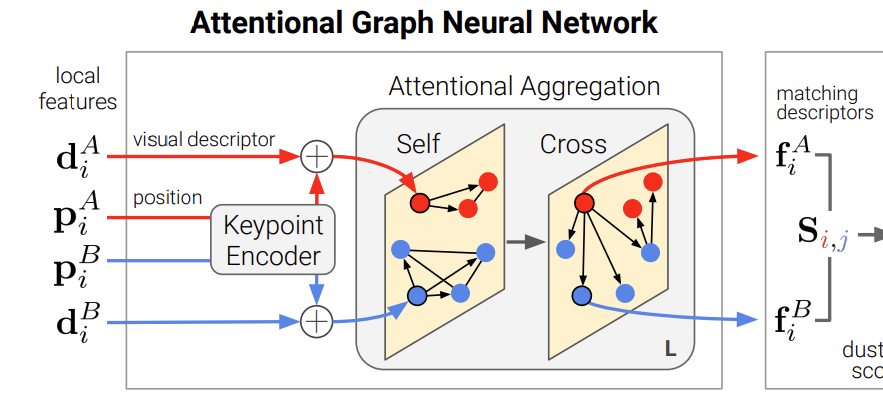
Keypoint Encoder

초기의 representation인 ^{(0)}\mathbf{x}_i는 시각적 외관 정보와 위치 정보를 결합하여 얻고, 두 값을 결합하기 위해 위치정보를 MLP를 이용하여 임베딩한 후 descriptor와 합쳐준다.

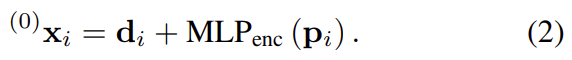
Multiplex Graph Neural Network

여러 레이어의 Graph Neural Network이다. 이때 keypoint는 노드가 되고, 2가지의 타입의 edge를 가지게 된다. (1) Intra-image edge(:self edge)는 동일 이미지 내의 keypoint들과 연결되고, (2)Inter-image edge(:cross edge)는 다른 이미지에 있는 keypoint들과 연결된다. 두 종류의 edge에 propagation을 위해 message passing formulation을 이용한다.(학습을 위해 활용한다..)

^{(l)}\mathbf{x}_i^A는 이미지 A의 중간 레이어\mathcal{l}의 representation으로, 다음 레이어로의 업데이트는 아래의 식으로 표현할 수 있다.

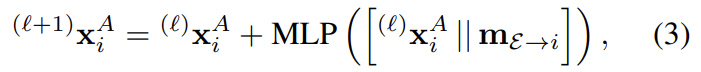
[· || ·] 는 두 값을 concat하는 것을 의미하고, message \mathbf{m}{\mathcal{E} \to i} 는 \mathcal{E}에 해당하는 keypoint들의 i에서의 aggregation으로, \mathcal{E}는 동일 이미지에 대한 \mathcal{E}{self}와 \mathcal{E}_{cross}를 번갈아가며 가지게 된다.(홀수일 때 self, 짝수일 때 cross라 함.)

Attentional Aggregation

attention을 aggregation하고 message \mathbf{m}_{\mathcal{E} \to i} 를 계산한다. retrieval과 유사한 방식으로, i의 representation인 \mathbf{q}_i는 key들인 \mathbf{k}_j에 대한 value \mathbf{v}_j를 가지게 되고, 가중평균을 이용하여 message를 구한다.

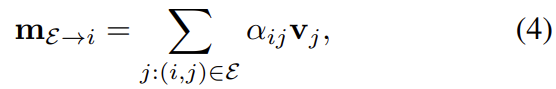
이때 \alpha_{ij}는 key-query의 similarity에 Softmax를 적용한 값이다. (\alpha_{ij} = \mathrm{Softmax}_j(\mathbf{q}_i^\mathsf{T},\mathbf{k}_j))

key,query,value에 대하여 keypoint가 해당하는 이미지 Q와 나머지 keypoint가 포함된 이미지S(self일 경우 Q, cross일 경우 다른 이미지를 의미함.)라 할 때, Graph Nueral Network의 deep feature의 linear projection으로 계산된다.

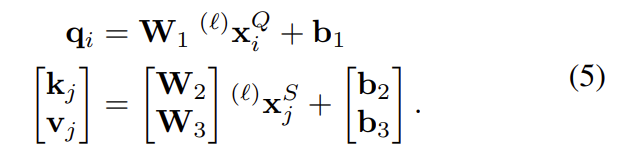
이를 통해 네터워크는 subset keypoint의 특성에 집중하여 flexibility를 최대화 할 수 있다.

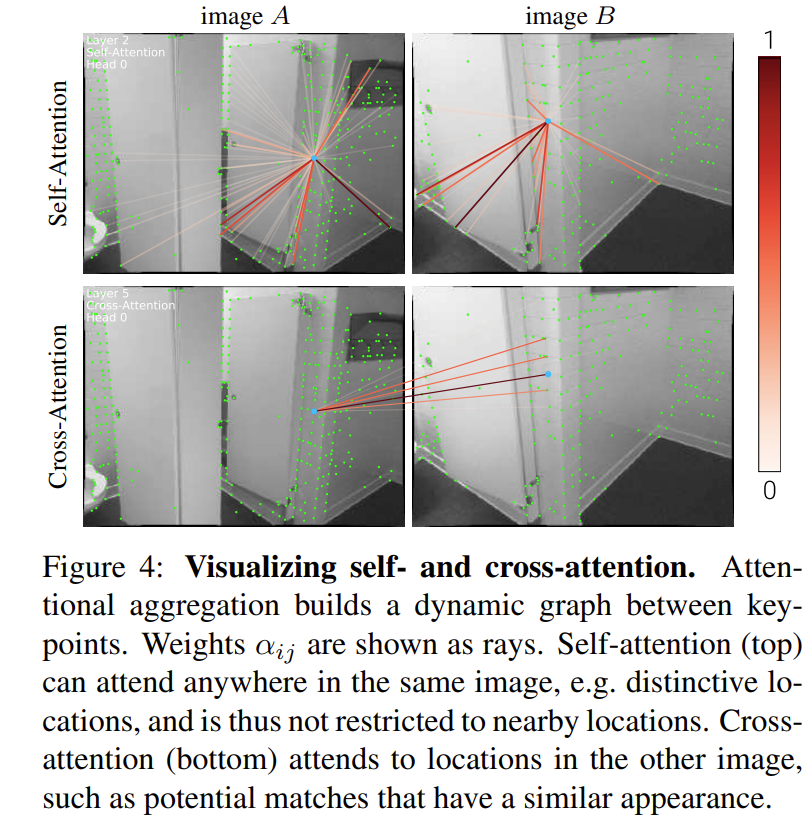
self-attention의 경우 구별되는 위치에 대하여 높은 가중치를 갖는 것을 확인할 수 있고, cross-attention에 대해서는 유사한 위치에 대하여 높은 가중치를 갖는 것을 확인할 수 있다.

최종적으로 descriptor는 L개의 레이어를 통과시킨 feature가 된다.

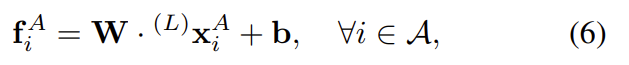
3.2. Optimal matching layer

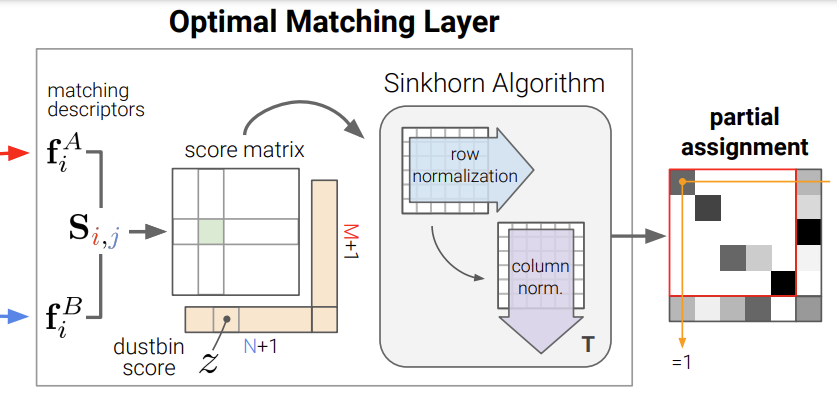
partial assignment matrix를 생성하기 위한 레이어이다.

Score Prediction

두 이미지 A와 B에서 얻은 representation을 내적하여 얻는다.

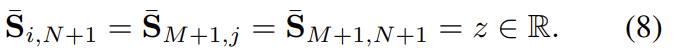
Occlusion and Visibility

일부 매칭이 되지 않는 keypoint에 대응하기 위하여 명시적으로 일치하는 keypoint를 dustbin이라는 것에 할당하게 된다. 이때 dustbin은 매칭이 되지 않는 경우를 표현하기 위한 것이다. 학습이 가능한 단일 파라미터로 채워진 N+1,M+1 행과 열을 추가하여 S를 \bar{S}로 늘린다. (즉 위의 그림에서 dustbin score에 해당하는 값은 모두 z로 동일하게 설정되는 것이다.)

또한 assignment \mathbf{P}도 \bar{\mathbf{P}}로 늘어난다.

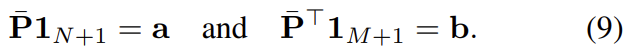
이때 \mathbf{a}와 \mathbf{b}는 다음과 같이 정의된다.

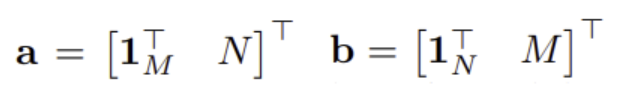
Sinkhorn Algorithm

최적화 문제를 해결하기 위해 sinkhor algorithm을 이용하였다. 행과 열을 따라 exp(\bar{\mathbf{S}})를 반복적으로 수행하여 정규화를 하였으며 T번 반복 후 dustbin이 아닌 부분은\mathbf{P}로 복원한다. 즉 이 과정을 통해 dustbin에 대한 값을 구한 것이라고 생각하면 될 것 같다.

3.3. Loss

Graph neural networ와 optimal matching 레이어는 설계상 미군 가능하여 역전파가 가능하다. supervised 방식으로 학습을 한다. \mathcal{I}와 \mathcal{J}는 일치하는 대응점이 없는 경우의 keypoint들의 집합을 의미한다.

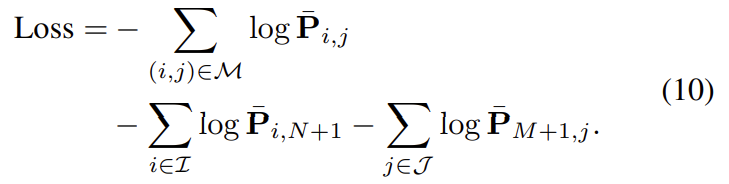
이를 통해 recall과 precision을 높이는 것을 목표로 한다.

4. Experiments

SuperPoint를 이용하여 keypoint를 detect하고 descriptor 추출하였다.

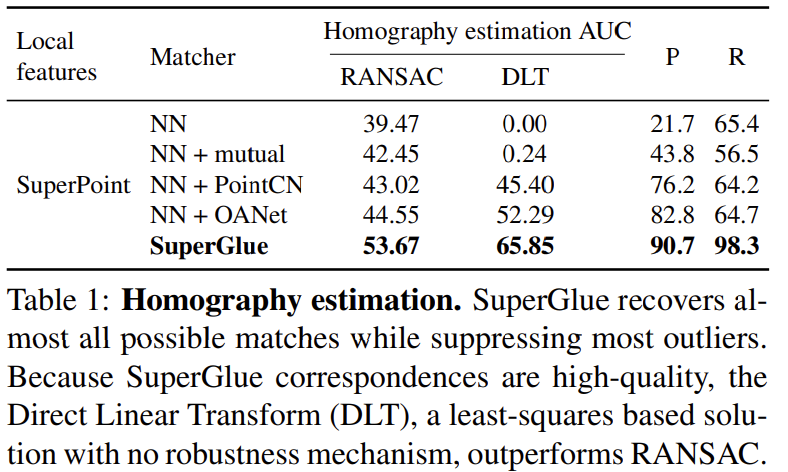
4.1. Homography estimation

실제와 합성 데이터를 이용하여 homograph 추정 실험을 수행하였다.

• Dataset: Oxford and Paris dataset random하게 homograph sampling을 하고, random한 photometric distortions을 적용하여 이미지쌍을 생성하였다.
• Metric: 네 모서리의 reprojection error의 평균을 계산하고 AUC(the area under the cumulative error curve)의 최대 10 픽셀까지 리포팅하였다.
• SuperGlue에서 높은 정확도와 리콜을 달성하였다.

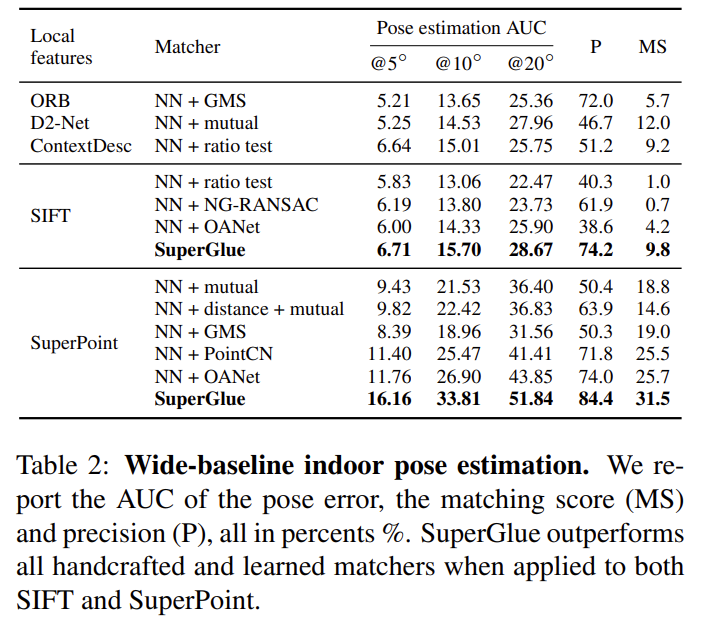
4.2. Indoor pose estimation

실내 이미지 매칭은 텍스처의 부족, 자기 유사성의 풍부함, 장면의 복잡한 3D 지오메트리 및 큰 시점 변화로 인해 매우 어렵다.

• Dataset: ScanNet 실측 포즈와 깊이 이미지가 있는 단안 시퀀스 데이터셋
• Metric: AUC
• SuperGlue에서 높은성능을 달성하였다. SuperPoint를 사용한 SuperGlue에서 SOTA를 달성하였다.

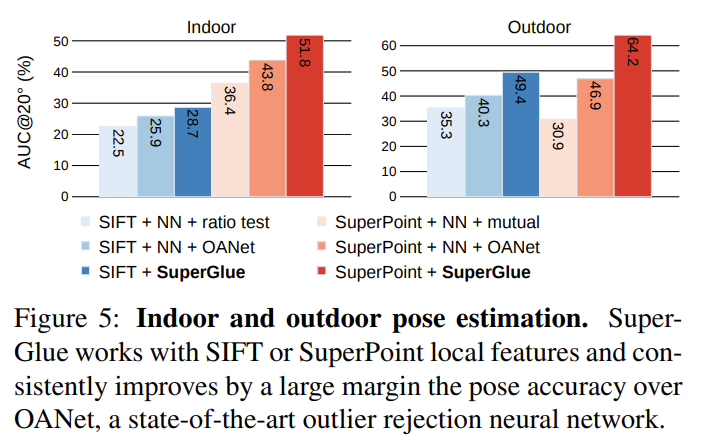
4.3. Outdoor pose estimation

• Dataset: YFCC100M dataset의 subset인 PhotoTourism dataset(CVPR19 Image MAtching Challenge 에서 사용한 데이터셋) 실측 poses정보와 sparse 3D model을 가짐.
• Metric: AUC
• SuperGlue가 SIFT와 SuperPoint 모두에 적용되었을 때 높은 성능을 보인다. 이때 매칭의 정확도가 매우 높아(84.9%) SuperGlue가 local feature를 잘 매칭시킬 수 있다는 것을 보인다.

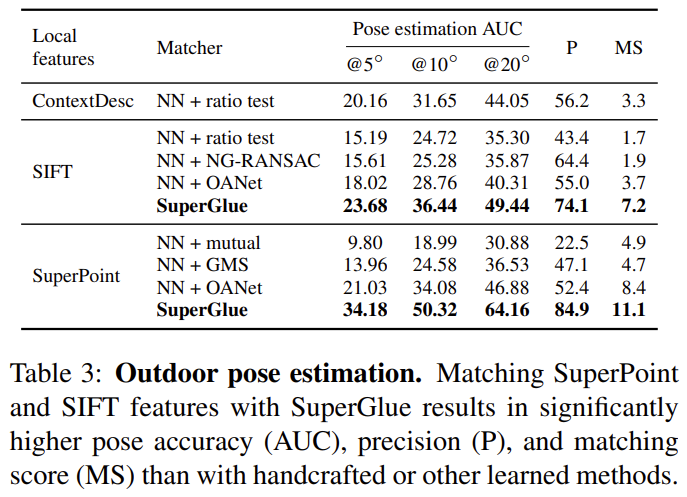
4.4. Ablation study

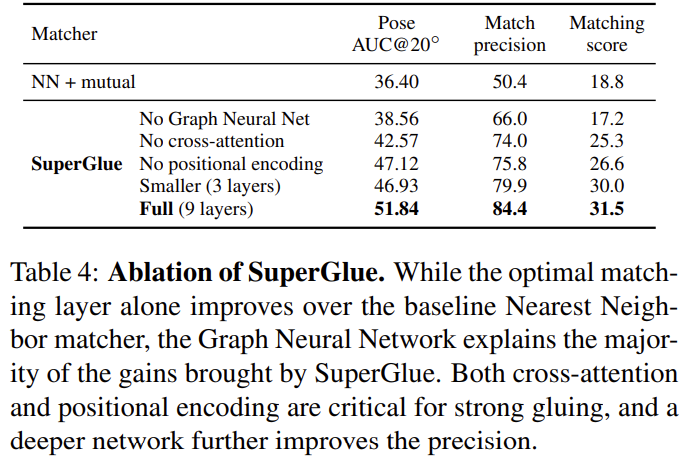
제안한 모듈에 대한 ablation study를 진행하였다. 대부분의 블록이 유용함을 보일 수 있었다.