조금 고전이지만, 제가 현재 하고 있는 연구에서 중요하게 사용하고 있는 연구이기에 이번 리뷰에서 설명하고자 합니다. 리뷰의 내용은 이곳을 참조하였습니다.

자 위에 두 개의 이미지가 있습니다. 두 이미지는 동일한 이미지이며, 밝기 차이를 나타내고 있습니다. 동일한 이미지에 대해서 가장 일반적인 그레디언트 기반 엣지 및 코너 추출 알고리즘인 Sobel 알고리즘을 통해서 엣지를 추출하면 다음과 같습니다.

엣지를 추출하고 normalization을 진행하면 동일한 엣지와 코너가 추출된것으로 보입니다. 그렇다면 각 엣지나 코너를 나타내는 부분의 값을 살펴보겠습니다.
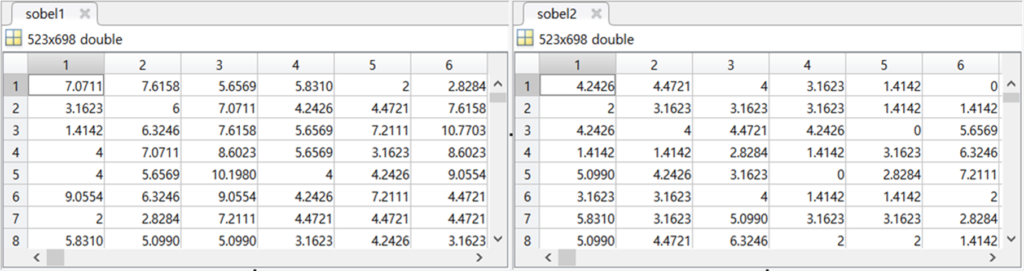
실제 값을 확인해보면 엣지라고 표기된 부분들의 값들에서 차이가 발생할 수 있는 것을 확인할 수 있습니다. 이는 normalization을 수행했음에도 불구하고, 실제 엣지를 나타내는 부분들의 값들은 contrast에 따라 다른 값을 나타낼 수 있음을 의미합니다. 그렇다면 본 리뷰의 제목인 Phase Congruency를 기반으로 엣지를 추출하면 어떻게 다를까요? 동일한 장면이지만 contrast만 다른 두 이미지에 대해서 Phase Congruency를 기반으로 엣지와 코너를 추출하면 다음과 같습니다.

앞서 Sobel의 결과와 비슷하게 두 영상에서 엣지나 코너가 잘 추출된것처럼 보입니다. 그렇다면 실제 값들의 분포는 어떻게 될까요?
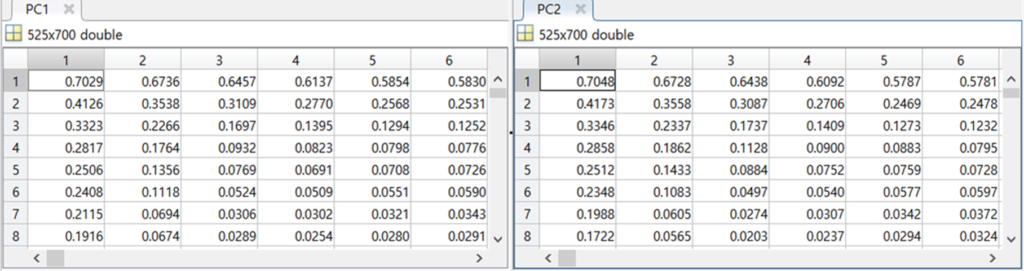
실제 두 영상에서 추출된 엣지영역의 값들이 거의 동일함을 확인할 수 있습니다. 이를 통해 Phase Congruency를 통한 엣지 혹은 코너 추출이 contrast 에 강인한 특징이 있음을 확인할 수 있습니다. 이러한 장점으로인해 다중 스펙트럼 연구분야에서 엣지 (or 코너) 추출을 위해 Phase Congruency가 많이 사용되고 있습니다.
자, 그렇다면 Phase Congruency 알고리즘을 통해 빛의 밝기에 강인한 엣지 혹은 코너를 추출할 수 있는 이유는 무엇일까요? 지금부터 Phase Congruency에 대해서 소개하도록 하겠습니다. Phase Congruency(위상 합동)은 이름에서도 알 수 있듯 Phase(위상)의 개념이 들어가고 이는 곳 주파수의 개념이 사용됨을 의미합니다. 갑자기 주파수(?)라고 하시는 분이 있을텐데, 아마도 우리의 기억속에는 희미하겠지만 다들 푸리에 변환을 배우신 기억이 있을 겁니다. 푸리에 변환을 직관적으로 설명하면 “임의의 입력 신호를 다양한 주파수를 갖는 주기함수들의 합으로 분해하여 표현하는것” 라고 정의할 수 있다고 합니다.

위의 그림에서 빨간색 성분은 공간축에 정의된 영상 신호입니다. 이때 해당 신호는 푸리에 변환을 통해 다양한 주파수를 갖는 주기함수들로 분해될 수 있습니다. 즉, 영상에서의 픽셀값들을 영상 신호로 정의하면 푸리에 변환을 통해 여러 sin,cos의 조합으로 나타낼 수 있음을 이야기합니다. 이때, 변환된 식은 실수부(cos), 허수부(sin)으로 구분되면 오일러 급수를 통해서 복소지수함수(ej2πux)로 표현하기도 합니다. 자세한 내용은 해당 블로그 에서 더욱 확인하실 수 있습니다.
이처럼 푸리에 변환을 통해 이미지를 주파수레벨로 분해할 수 있게 됐고, 이는 사람의 시각적 특징의 메커니즘과 굉장히 유사하다고 합니다. (연구) 이렇게 얻은 주파수 정보를 가지고, 위상이 일치하는 부분을 계산하려면 어떻게 할 수 있을까요? 푸리에 변환을 통해 얻은 주기함수를 통해 한 신호의 특정 지점에서의 위상 일치를 극좌표에 나타내면 다음과 같습니다.

위의 그림에서 x축은 실수부, y축은 허수부를 나타내며, 세타는 주기함수 벡터의 방향 즉 위상(Phase)를 나타내며, 크기는 주파수의 진폭(Amplitude)를 나타냅니다. 각 주기함수를 벡터로 표현할때 벡터의 합은 E(x)를 나타내며, 이를 로컬 에너지라고 명명합니다. 그리고 각각 벡터의 크기는 An으로 나타내는데, 만약 모든 벡터의 크기가 일관됐다면 로컬 에너지의 크기는 커지게 되고, 각 벡터 크기의 합과 유사해지므로 최대 1의 값을 가지게 됩니다. 반대로 모든 벡터의 방향이 다르다면 로컬 에너지의 값은 작아지며 0에 가까운 값을 가지게 됩니다. 이처럼 각 벡터(위상)의 합(일치)를 나타내는 것을 phase congruency라고 명명하며 이를 수식으로 나타내면 1차원의 경우 아래와 같이 나타낼 수 있습니다.
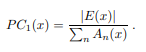
이 수식은 앞서 설명한 사람의 시각과 유사한 특징을 갖는다고 발표한 네이처 논문에서 정의됐으나, 해당 논문의 저자는 이러한 수식이 노이즈에 취약하며 좋은 localization을 제공하지 못한다고 이야기 합니다. 따라서 해당 논문의 저자는 이전 연구에서 기존 phase congruency 계산 방식을 개선한 새로운 phase congruency 계산식을 제안합니다.
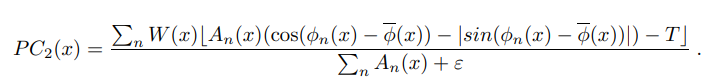
앞서 설명에서 phase congruency가 무엇이고, 어떻게 계산하는지 나타냈다면 이를 이용하여 최종적으로는 영상에서 엣지나 코너를 어떻게 예측할 수 있을까요? 앞서 설명한 방법은 1D 신호에 대한 phase congruency를 구하는 방식이므로, 2D 영상에 대한 phase congruency를 계산하기 위해서는 영상 내에서 여러 방향으로 1D 영상 신호를 정의하고 각각에 대하여 phase congruency를 계산한 후 결합하는 과정이 필요합니다. 그리고 해당 논문에서는 이러한 1D 신호의 방향을 정의하는데 사람의 시각 피질 내에 있는 세포의 수용계를 수학적으로 모델링하기 위해 사용된 필터라고 합니다. 논문에서는 이 중 전형적인 6개의 방향에 대한 필터를 이용하여 이미지(2D)에서 1D 영상 신호를 추출했다고 합니다. 그리고 각 방향의 독립적인 phase congruency를 계산하고 이에 대한 모멘텀의 변화를 이용하여 coner와 edge를 추출했다고 합니다(?) – 사실 이해하기가 어려워서 조금더 시간이 필요할 것 같습니다.자세한 내용이 궁금하신 분들은 논문을 함께..



실험 파트에서는 자신들의 방법을 그레디언트 기반 엣지 검출 알고리즘인 해리스 코너와 비교하여 강인함을 나타내고 있습니다.
해당 페이퍼를 전체적으로 이해하기에는 제 배경지식이 아직 부족하여.. 추후 계속적으로 읽어보고 해당 리뷰를 업데이트해보도록 하겠습니다.