이제 본격적으로 최적화에 대해서 알아보도록 하겠습니다. 이전까지는 Convex Set이 무엇인지 그리고 Convex Function이 무엇인지 알아보는 과정을 거쳤습니다. 그러한 지식을 바탕으로 이제 최적화가 무엇이고 그 중 Convex Optimization이 무엇인지 알아보도록 하겠습니다.
정확히는 최적화 알고리즘들에 대해서 배우는 것은 아니고 문제가 어떻게 정의 되는지 정도로만 얘기할 것 입니다.
Lecture 4 : Convex Optimization Problems
Optimization problems
그렇다면 일단 최적화 문제가 무엇인지 알아보는 것부터 시작하겠습니다. 여기서 General한 Optimization의 형태는 아래와 같습니다.

일단 우리의 목적함수(objective function) 혹은 비용함수(cost function) f_{0}(x)가 존재합니다. 그래서 보통 최적화는 이 목적함수를 최소화하는 x를 찾는 것이 목표인데, 이 x는 constraints를 만족해야 합니다. constraints는 optimization 변수 x가 만족해야하는 조건이라 보면 됩니다.
f_{i}(x)\leq 0,i=1,\ldots ,m는 inequality constraints 라고 정의합니다. h_{i}(x)=0,i=1,\ldots ,p는 equality constraints 라고 정의됩니다. 그래서 optimization problem에 모든 constraints를 만족하는 집합을 feasible set이라고 정의합니다.
D=\bigcap^{m}_{i=0} dom(f_{i})_{\bigcap }\bigcap^{p}_{i=1} dom(h_{i})이 feasible set이 되겠네요. 그리고 이 feasibile set이 optimization problem의 정의역이 되는 것 입니다.
그리고 우리의 목적은 Optimization Problem에 해당하는 최적의 솔루션(Optimal Value)를 찾는 것입니다.
- p^{\ast }=\inf\left\{f_{0}\left(x\right) | f_{i}\left(x\right)\leq 0,i=1,\ldots,m, h_{i}\left(x\right)=0,i=1,\ldots ,p\right\}
그리고 이 최적의 솔루션은 여러개일 수 있습니다. 다음으로는 극소점(locally optimal)에 대해서 알아보도록 하겠습니다. 극소점은 그 지역에서만 optimal한 값으로 작은 반경 R에 대해서는 가장 작은 값을 가지는 point라 보시면 됩니다.
- f_{0}\left( x\right)=\inf \left\{f_{0}\left(z\right) | f_{i}\left(z\right)\leq 0, i=1,\ldots ,m,h_{i}\left(x\right)=0 , i=1,\ldots ,p,\| z-x\|_{2}\leq R\right\}

그래서 지금까지 일반적인 최적화 문제는 어떻게 정의가 되는지 알아봤습니다.
일반적인 최적화 문제는 그 문제가 feasible 한지 아닌지 알아봐야 하는데요. 무슨 소리냐면 Constraints를 만족하는 x가 있는지 없는지 확인해야 한다는 소리입니다. 일반적인 최적화 문제에서는 feasible set이 공집합일 수 있다고 합니다. 즉 해가 없다는 문제라는 소리겠죠.
그래서 constraints를 만족하는 x가 하나라도 존재한다면 그 문제는 solvable problem이 되는 것이고 아니면 insolvable problem이 되는 것 입니다. 당연히 앞으로의 내용은 feasible set이 존재하는 문제에 대해서 다룰 예정입니다.
Equivalent problems
이제 최적화 문제 중 Equivalent problem에 대해서 알아보도록 하겠습니다. Equivalent problem이란 서로 다른 두 최적화 문제가 서로 같은 해를 가진다는 문제 입니다. 그래서 어떻게 활용 될 수 있나면 우리가 잘 알고 있고 풀기 쉬운 문제로 해를 먼저 찾고 이 쉬운 문제와 Equivalent한 관계에 있는 문제에 대입해서 바로 해를 찾을 수 있다는 소리입니다.
쉬운 문제로 정답을 찾고 다른 문제에 접근하는 방식인데 여기서 중요한 것은 두 문제가 Equivalent라는 것이 증명이 되어야 한다는 것 입니다.
그래서 Equivalent problem을 만들어내는 몇가지 transformation이 존재하는 데 그것들에 대해서 같이 알아보겠습니다.
Change varialbes
변수 변환 입니다. 일대일 대응 관계로 변수변환 함수가 존재한다면 Optimization Problem의 해를 찾고 그 Optimal point를 일대일 대응 함수에 넣어서 새로운 해를 찾을 수 있겠죠. 최적화 변수를 새롭게 mapping 해주는 함수 \phi (z)=x,\phi^{-1} (x)=z만 찾을 수 있다면 가능한 방법입니다.

Transformation of objective and constraint functions
다음으로는 objective function과 constraint function을 조금 변형 시키는 경우입니다. 이 목적함수를 변형시킬 때는 무조건 단조증가(monotone increasing) 함수로 변형을 해야합니다.
무슨 소리나면 우리의 새로운 목적함수 \tilde{f_{0}}(x)=\psi_{0}(f_{0}(x))가 단조 증가함수라면 이 함수의 최소지점은 정의역이 최소가 되는 부분입니다. 그리고 이 정의역이 최소가 된다는 것은 우리의 원래 목적함수를 최소화하는 것과 같은 맥락이죠.

Slack variables
Inequality constraints를 equality constraints로 만들어주는 것 입니다. 원래 f_{i}(x)\leq 0는 0\leq s_{i}에 대해서 f_{i}(x)+s_{i}=0 이렇게 equality constraints로 변경할 수 있습니다. 여유 변수를 새롭게 도입해서 inequality constraints를 equality constraints로 변경한 방식입니다.

Eliminating equality constraints
변수변환과 더불어 equality constraints를 동시에 없애주는 방식입니다. 즉, 변수변환 + h_{i}(x)=0을 동시에 만족시키는 매개함수 x=\phi (x)를 찾아주는 것이 핵심입니다. 그런데 이 x=\phi (x)를 찾아주는 것이 쉽지는 않겠죠. 이렇게 해서 새롭게 Equivalent한 problem에는 inequality constraints만 존재하게 됩니다.

Eliminating linear equality constraints
자 여기서는 동일하게 equality constraints를 제거해주는 것이 목적인데, equality constraints가 Affine function 일 때의 경우 입니다. 원래 original problem의 equality constraints를 Ax=b라 하겠습니다.
그리고 임의의 행렬 F\in R^{n\times k} , Range(F)=Null(A)이 있다고 가정해보겠습니다. F의 Column space가 A의 Null Space에 해당하는 것이죠. 따라서 AFz=0이 성립합니다.
그리고 나서 원래 original problem의 equality constraints Ax=b를 만족하는 x를 x_{0}라 가정하겠습니다. 이때 우리의 최적화 변수 x를 x=Fz+x_{0}라고 두면 A(Fz+x_{0})=0+b=b가 항상 성립하기 때문에 equality constraints를 지워도 됩니다. 단 F를 잘 찾는 것이 중요하겠죠.

Optimizing over some variables
예를 들어 우리의 목적함수에 변수가 x , y만 존재한다고 가정하겠습니다. 이때 목적함수를 x,y에 대해서 최적화 시키는 것은 먼저 x를 상수로 고정해놓고 y에 대해서 최적화를 진행한다음 x로 최적화 하는 것과 같은 이치 입니다.
아래의 그림으로 먼저 감을 잡을 수 있는데요.
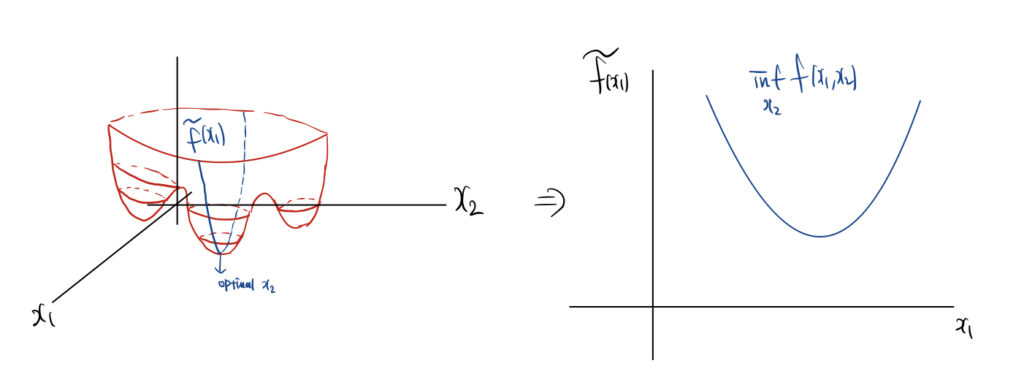
f(x_{1},x_{2})가 있을 때 우선 x_{1}를 상수로 고정하고 최적의 x_{2}를 찾은 다음 그 최적의 x_{2}로 픽스를 시킨 \tilde{f} (x_{1})에 대해서 x_{1}가지고 최적화를 진행하는 것 입니다.

이와 비슷하게 작동하는 alternating optimization 기법이 있는데요. 그 방법은 global minima를 보장할 수 없다고 합니다. 이와 반대로 지금 설명한 방식은 global minima를 이론적으로 보장할 수 있다고 하네요.
Epigraph problem form
마지막으로 Epigraph 형태로 문제를 변경할 수 있습니다.

자 문제가 f_{0}(x)\leq t 이렇게 있을 때 t를 최소화하는 것은 f_{0}(x)를 최소화 하는 것과 같습니다.
Convex Optimization
위에서는 일반적인 최적화 상황에 대해서 다루었고 이제는 Convex optimization에 대해서 얘기해보도록 하겠습니다. 이번글에서는 간단히 소개정도로만 할 것이고 다음 글에서 차차 구체적인 예시와 어떤 알고리즘들이 있는지 알아보도록 하겠습니다.
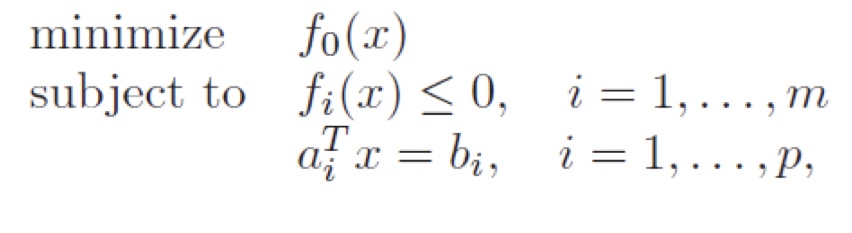
- 우선 목적함수 f_{0}(x)가 Convex function이어야 합니다.
- inequality constraints f_{i}(x) 역시 convex function이어야 합니다.
- equality constraints a^{T}_{i}x-b_{i}=0 는 affine function이어야 합니다.
- 마지막으로 feasible set이 convex set 이어야 합니다.
여담으로 Concave maximization problem 역시 Convex Optimization이라 볼 수 있습니다.
Global optimal = Locally optimal
Convex Optimization이라는 것이 증명이 된다면 가장 중요한 성질이 있었죠. Global Optimal을 무조건 구할 수 있다라는 성질이 있었습니다.
Proof)
그렇다면 “Global optimal = locally optimal” 이 정말로 성립하는 지 증명을 통해 알아보도록 하겠습니다.
우선 feasible point x에 대해서 x가 locally optimal point라 가정하겠습니다.
- f_{0}(x)=\inf \left\{ f_{0}\left( z\right) | z is feasible,\| z-x\|_{2} <R\right\} ,for some R>0
그런데 여기서 x는 locally optimal 이지, global optimal이 아니라고 가정해보겠습니다. 그리고 우리는 이 가정이 모순이라는 것을 밝혀서 결국 “Global optimal = locally optimal” 라는 것을 밝히도록 하겠습니다.
새로운 y를 등장시키도록 하겠습니다. 이 y를 우리는 global optimal 이라 정의하겠습니다. 그러므로 아래의 부등식이 성립합니다.
- f_{0}(y)<f_{0}(x)
그런데 이때 x와 y의 거리는 R보다 커야 합니다. 만약에 R보다 작다면 x가 극소점이라는 가정에 위배되기 때문입니다.
- \| y-x\|_{2} >R
그리고 이 상황에서 x와 y사이에 있는 z=\left( 1-\theta \right) x+\theta y를 고려하면서 정확히 x와 y 절반에 위치하도록 \theta =\frac{R}{2\| y-x\|_{2} } 를 이렇게 정의해주겠습니다.
- \| z-x\|_{2} <R
즉, z는 x와 x의 반경 내부에 들어와있기 때문에 f_{0}\left(x\right) \leq f_{0}(z)가 성립해야 합니다. 하지만 Convex optimization 같은 경우는 목적함수가 Convex function이기 때문에 정의를 이용하면
- f_{0}(z)\leq \left( 1-\theta \right) f_{0}(x)+\theta f(y)\leq f_{0}(x)
이렇게 됩니다. 하지만 이는 f_{0}\left(x\right) \leq f_{0}(z) 여기에 위배되는 상황이기 때문에 애초에 우리가 가정했던 x 말고 다른 global optimal이 있다 라는 가정은 참이 아닌것으로 증명이 됩니다.
고로 Convex optimization에서 x가 locally optimal 이라면 그와 동시에 global optimal 이라는 것이 증명되었습니다.
Optimality criterion
다음으로는 목적함수 f_{0}가 미분가능한 함수일때 optimal point를 결정짓는 optimally criterion 하나를 소개하도록 하겠습니다. 우선 f_{0}가 Convex function이기 때문에 first order condition을 만족하게 됩니다.
- f_{0}(x)+\nabla f_{0}(x)^{T}\left(y-x\right)\leq f_{0}\left(y\right)
여기서 만약에 x가 optimal solution이라 가정한다면 f_{0}(x)\leq f_{0}\left(y\right) 이 항상 성립합니다. 그런데 이게 항상 성립되기 위해서는 0\leq \nabla f_{0}(x)^{T}(y-x)이 만족해야 합니다.
- 0\leq \nabla f_{0}(x)^{T}(y-x)
따라서 이 조건이 성립한다면 x는 optimal point 입니다. 기하학적으로 간단하게 설명하면 (y-x) 벡터와 x의 그래디언트의 코사인이 항상 양의 값을 가진다는 의미로 사이각이 예각이라는 뜻입니다. 여기서 다루는 Optimality Criterion 말고도 뒤에서 몇가지 중요한 Optimality Condition들을 다룰 예정인데 그건 그때가서 또 자세히 얘기해보도록 하겠습니다.
Proof)
우선 여기서 다룬 이 Optimality Criterion이 성립하는지 증명을 한번 같이 해보도록 하겠습니다.
우리가 증명하고 싶은것은 x가 optimal point일 때 f_{0}(x)\leq f_{0}\left(y\right) 이 성립하는지를 알고 싶은 것이고 반대로 f_{0}(x)\leq f_{0}\left(y\right) 이 성립할 때 x가 optimal point 인지 알아보는 것 입니다.
x가 optimal point일 때 f_{0}(x)\leq f_{0}\left(y\right) 이 성립하는 것은 위에서 살펴봤고, 이제 f_{0}(x)\leq f_{0}\left(y\right) 이 성립할 때 x가 optimal point 인지 알아보겠습니다.
우선 x가 optimal point 일 때 0>\nabla f_{0}(x)^{T}(y-x)이 성립한다고 가정해보도록 하겠습니다. 이번에도 반대의 상황을 가정하고 이것이 모순됨을 보이는 것이 증명의 방향입니다.
- 0>\nabla f_{0}(x)^{T}(y-x)
그리고 나서 z(t)=ty+\left(1-t\right)x 이렇게 line segment를 정의했다가 f(z(t))=f(ty+\left( 1-t\right) x)이것을 t=0일 때의 미분을 구해보겠습니다. g(0)=x이기 때문에 x 근방에서의 증감을 확인하기 위함입니다.
- \frac{d}{dt} f_{0}(z(t))|_{t=0}=\nabla f_{0}(x)^{T}(y-x)<0
자 f_{0}는 x 근방에서 감소함수라는 뜻입니다. 하지만 x 근방의 아주 작은 양의 값 t에 대해서도 x가 optimal point이기 때문에
- f_{0}(x)<f_{0}(z(t))
이 성립해야 하지만 이는 x 근방에서 감소함수라는 것에 대해서는 모순이죠. 즉, 처음에 했던 가정 0>\nabla f_{0}(x)^{T}(y-x)이 모순이고 원래 0\leq \nabla f_{0}(x)^{T}(y-x)이 만족한다는 것을 우리는 알 수 있습니다.
여기까지 증명한 것은 Convex optimization이 Inequality Constraints와 Equality Constraints가 존재할 때 Optimality Criterion이었습니다. 만약에 Convex optimization이 Unconstrained problem이라면 굉장히 쉽게 풀 수 있습니다. \nabla f_{0}(x)=0 지점이 global optimal 입니다. 증명은 간단하니 직접 해보시길 바랍니다.
여기까지 해서 간단하게 Convex Optimization이 무엇인지 얘기했습니다. 일단 X-Review로 최적화 이론을 다루는 것은 여기까지로 하고 또 기말고사 시즌이 오면 한번 짧고 굵게 다시 정리하도록 하겠습니다.
감사합니다.