[ICLR2022](Spotlight) How Do Vision Transformer Work?

네 이번에 리뷰할 논문은 Transformer와 CNN을 비교하여 각각의 특성을 분석한 논문을 가져왔습니다. 조원 연구원님이 공유해주셔서 알게되었는데 생각보다 매우 내용이 알차고 좋은 논문이었습니다. 얼핏 내용만 봤을 땐 지난번에 ConvNeXt 논문과 비슷한 특성을 보이는 것 같아 보이긴 하지만, 실제 내용은 ConvNeXt와 비슷한 의미로 충격적이며 시사하는 바는 매우 다른 논문이니 한번쯤은 꼭 읽어보셨으면 합니다.

Intro

해당 논문에서 저자는 먼저 ViT에 대한 기존의 상식적인 내용들을 토대로 몇가지 질문에 대한 답을 내놓습니다.

1. Q : Multi-head Self Attention(MSA)는 모델 성능 또는 최적화 관점에서 어떤 역할을 수행하나?
   A : Long-range dependency를 모델링할 수 있기 때문에 성능도 좋아지고 다양한 task에서 잘 동작한다.
2. Q : MSA는 Conv처럼 될 수 있나?
   A : MSA는 컨볼루션으로 표현할 수 있기 때문에 컨볼루션이랑 매우 유사하게 동작할 수 있다.
3. Q : MSA를 Conv과 어떻게 조합하여 사용할 수 있을까?
   A : 만약 조합해서 사용하게 된다면, 아무래도 추상적인 정보가 많이 포함된 high-level feuatre에서 MSA를 사용하는게 좋지 않을까 싶다.

자 이것이 주어진 질문에 대하여 저희가 생각하는 transformer의 상식선에서 답변할 내용들입니다. 하지만 저자는 이러한 답변들은 사실 다 잘못된 것이며, 해당 논문에서는 위의 질문들에 대하여 올바른 답변을 하기 위한 다양한 실험들을 보여주는 방식으로 논문이 진행됩니다.

Q1 : What Properties of MSAs Do We Need To Improve Optimization?

저자가 말하는 Self-attention은 loss를 평평하게 만든다(landscape)

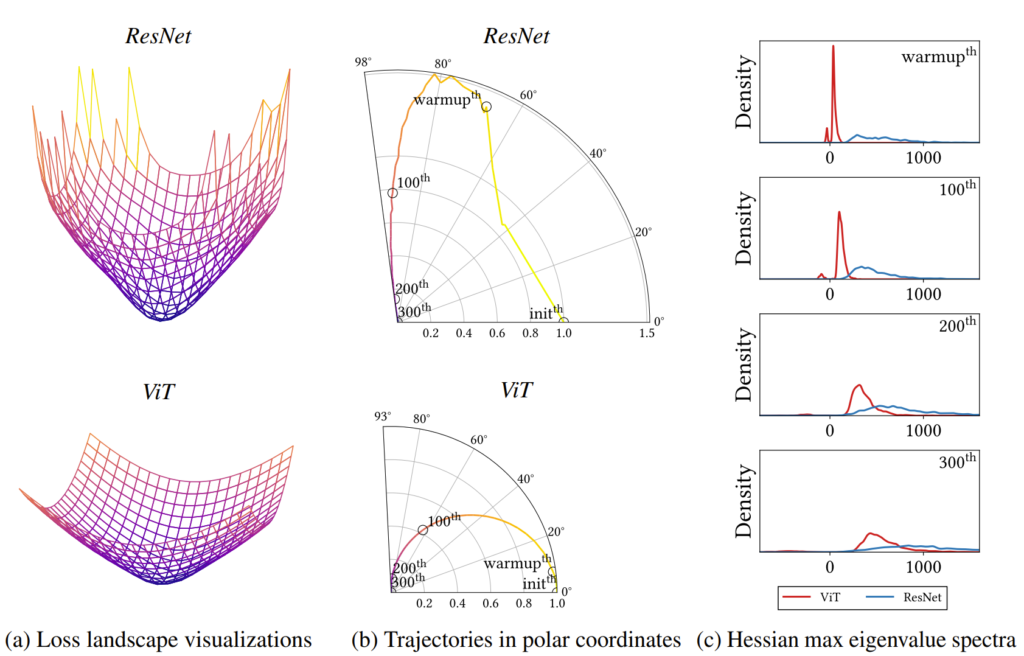
그림1-(a)에서는 두가지를 주목해야함. 먼저 첫째로 가장자리가 매끄러울 수록 좋고, 둘째로는 optima 부분이 평평할 수록 좋은 것. (b)는 논문에서 제안하는 learning trajectory visualization 방식으로, 화살표 방향으로 시작되는데 이때 ResNet은 산만한 반면, transformer는 부드럽게 움직이는 모습입니다. (c)의 경우도 논문에서 제안하는 방식이며 네트워크의 Hessian을 통해서 loss landscape를 찾는 방법임.

Hessian이란 무엇인가?

Hessian(또는 Hesse) Matrix는 어떠한 함수의 이차 미분을 의미합니다. 즉 함수의 곡률(Curvature)특성을 나타내는 행렬로 볼 수 있는데, 이 행렬이 인공지능에서는 critical point의 종류를 판별하는데 활용된다고 합니다.

참고로 Critical Point는 어떤 함수의 일차미분 값이 0이 되는 지점을 의미하며, 저희가 잘 아는 극대점, 극소점 그리고 안장점(saddle point) 등이 이에 해당합니다. 극대 극소는 많이 들어봤는데, saddle point는 또 뭘까요? 이에 대해서는 그림2를 보면서 설명드리겠습니다.

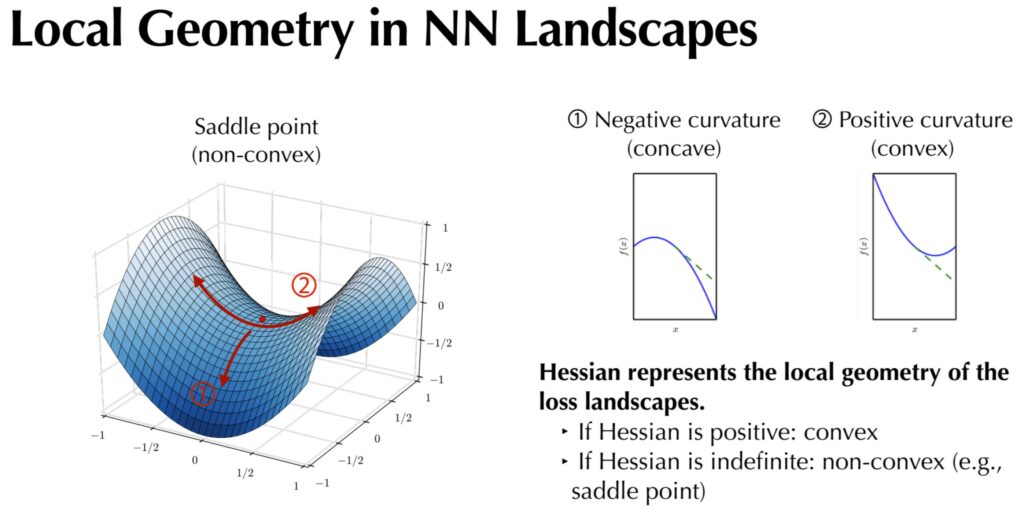
그림2 좌측에는 어떠한 안장 형태의 그래프가 그려져있습니다. 해당 표면에서 붉은색 점이 하나 있는데 저 붉은색 위치는 위로 볼록한 지점이기도 하며(1번방향을 기준), 아래로 볼록한 지점이 될 수도 있습니다(2번방향 기준)

이처럼 위로 볼록한 지점과 아래로 볼록한 지점이 동시에 위치하는 지점을 saddle point(안장점)이라고 명칭합니다. 참고로 위로 볼록한 경우만 있을 때는 극대점(maxma), 아래로 볼록한 경우만 있을 때는 극소점(minima)이라고 합니다.

자 그러면 일차미분 값이 0이 되는 지점 중, 어떤 값이 극대, 극소 또는 안장점인지를 어떻게 알 수 있을까요? 이를 구분하기 위해서 사용되는 개념이 바로 Hessian matrix입니다.

구하는 방법은 다음과 같습니다. 먼저 critical point에서 Hessian 행렬을 계산한 뒤 그 행렬의 모든 고유값(eigenvalue)들이 어떤 부호를 가지고 있는지를 통해 확인할 수 있으며 아래와 같습니다.

1. critical point에서 구한 Hessian 행렬의 eigenvalue가 모두 양수이면 극소점이다.
2. critical point에서 구한 Hessian 행렬의 eigenvalue가 모두 음수이면 극대점이다.
3. critical point에서 구한 Hessian 행렬의 eigenvalue가 양수,음수 모두 가지면 안장점이다.

이정도면 대충 saddle point의 개념 및 Hessian matrix의 활용처에 대해 이해하셨을 것이라고 판단됩니다. 아무튼 Saddle point는 loss landscape에서 많으면 많을수록 수렴을 하기 어렵게 만들게 됩니다.

왜냐하면 Optimization의 가장 기초이자 목표가 바로 convex한 영역 즉 minima를 찾아가는 과정인데, saddle point의 경우에는 minima와 maxima가 동시에 위치하여 자칫하면 모델이 global minima에 수렴을 못해버리는 non-convex한 영역이기 때문입니다.

또한 Hessian matrix를 통해 우리는 loss의 landscape가 얼마나 굽었는지 역시도 알 수 있습니다. 이는 위에서 언급했듯이 Hessian matrix가 함수의 곡률을 나타내기 때문이죠.

요약하자면 Hessian matrix의 eigenvalue 값의 크기로 얼마나 굽었는지를 확인할 수 있으며, 부호를 통해 해당 지점이 saddle point인지 minima인지를 확인할 수 있습니다. 그리고 저자는 이러한 특성들을 이용해서 Transformer와 Convolution의 특성들을 분석하고자 합니다.

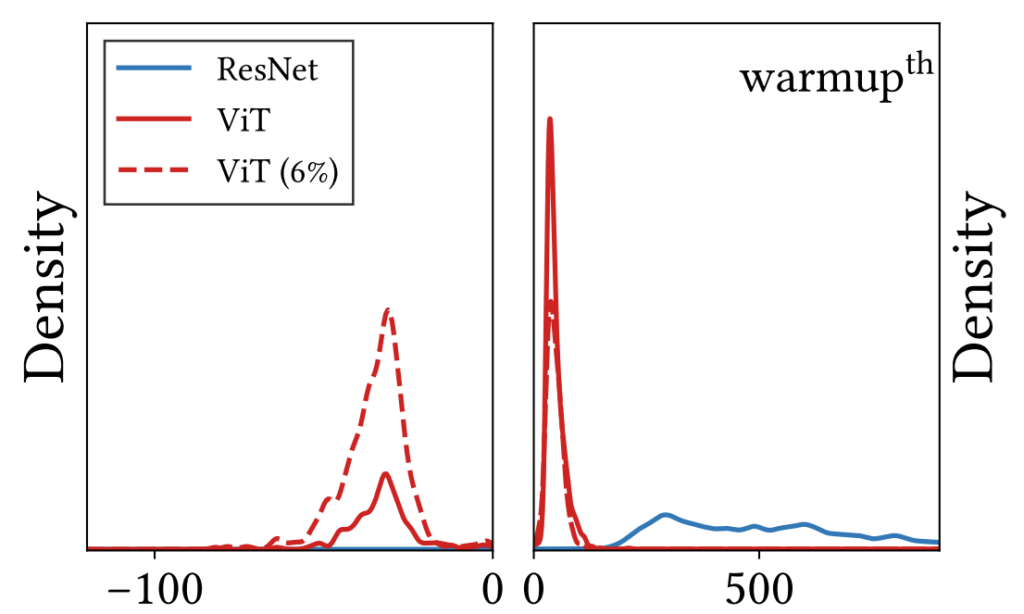
그림3은 CNN과 ViT 모델에 대하여 2가지 측면을 분석하고자 한 그림입니다. 먼저 첫째로는 loss의 landscape가 어떠한 convexity를 가지는지를 negative max hessian eigenvalue 분포(면적)를 통해 확인할 수 있으며 둘째로 곡률을 확인하기 위하여 positive max hessian eigenvalue의 평균값을 사용할 수 있습니다.

그러면 그림3을 보고 ViT와 ResNet의 특성들을 분석해보겠습니다. 먼저 그림3 좌측을 보면 ResNet은 음의 hessian eigenvalue를 거의 가지지 않는 반면에 ViT는 상당히 많은 양의 negative 값을 가지고 있습니다. 이는 Transformer가 CNN과 비교하여 loss의 landscape이 non-convex 하다는 것을 의미합니다.(ViT의 단점)

또 곡률 측면에서 보았을 때 그림3 우측과 같이 ViT는 Positive max hessian eigenvalue의 평균이 0에 가까운 작은 값들인 반면, ResNet은 전반적으로 값들이 큰 것을 볼 수 있습니다. 이러한 점은 Transformer 특히 Multi-head Self-Attention(MSA)이 loss의 landscape를 평탄화해줌을 의미합니다.(ViT의 장점)

그림3에서 붉은색 점선은 ViT 모델을 학습시킬 때 오직 6%의 traindata set만을 사용했다는 것입니다. ViT는 잘 아시다시피 data hungry 특성이 매우 강한 모델인데 저자는 data 양이 부족하게 될 경우 모델의 negative hessian eigenvalue들이 더 넓은 분포를 가진다는 것을 확인했습니다.

즉 ViT는 데이터 셋이 부족하게 되면 loss landscape에 saddle point가 많아져서 학습이 어려워진다고 볼 수 있겠군요.

위에 실험을 정리해보겠습니다. ViT는 negative hessian eigenvalue분포를 줄이는 조치를 취해서 saddle point를 최대한 적게 만들어야 모델 성능이 오를 것이며, ResNet은 positive hessian 값들의 크기를 줄여서 곡률이 완만해지는 조치를 취해야 한다는 것이네요. 즉 여기서 CNN과 Transformer는 서로의 장단점이 명확한 것을 확인할 수 있습니다.

그렇다면 두 모델은 왜 이렇게 서로 다른 특성을 가지게 되는 것일까요? 흔히 잘 알려진 사실인 CNN과 Transformer의 가장 큰 차이를 꼽자면 CNN의 local recpetive field로 인한 strong inductive bias와 Transformer의 MSA를 통한 weak inductive bias의 차이가 있죠.

저자는 이러한 차이로 인해 두 모델은 장단점이 분명한 특성을 가지고 있으며 Transformer의 weak inductive bias가 항상 더 좋아서 Transformer가 좋다 라고 주장할 수는 없다 말합니다.

그렇다면 Transformer는 어째서 landscape를 잘 평탄화 할 수 있을까요? MSA를 통한 long-range dependency 덕분이지는 않을까요? 저자는 이러한 질문에 대한 답을 하기 위해 또 다른 실험을 진행합니다.

먼기존 ViT는 전체 Feature map에 대하여 MSA 연산을 수행하기 때문에 Global Receptive Field를 가진다고 볼 수 있습니다. 저자는 여기서 Long-Range Dependency의 영향력을 보기 위해 MSA 연산을 local한 방식으로 변경하였습니다.

참고로 커널 사이즈가 8×8일 때를 global MSA라고 지칭하며, 5×5, 3×3으로 점점 작아질수록 long-range dependency가 줄어든다고 보시면 됩니다.

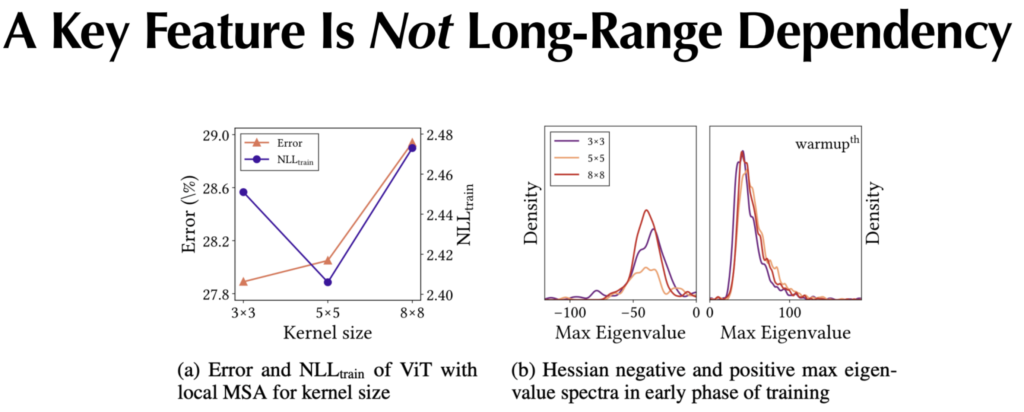
자 그러면 그림4-(a)에 대해 살펴보도록 하겠습니다. (a)는 local로 변경하였을 때 train set에서의 NLL loss값과 test셋에 대한 accuracy error 값을 나타낸 것입니다. 일반적으로 local한 경우에 더 성능이 올라간 것을 볼 수 있으며, 사실 이러한 결과는 Swin Transformer나 다른 방법론들에서도 나온 결과이긴 합니다. 즉 local MSA가 더 좋은 성능을 보인다는 것이죠.

하지만 저자는 test뿐만 아니라 train에서도 local MSA가 더 성능이 좋다는 것에 집중합니다. 왜냐하면 local MSA가 왜 성능이 더 좋은가?에 대하여 기존 방법론들은 local MSA가 일종의 regularization 효과를 가지고 있기 때문에, test에 대하여 성능이 잘 오른다 라고 주장하였지만, 만약 그 주장대로라면 train에서는 loss가 더 커져야하기 때문입니다.

하지만 저자는 train loss도 함께 잘 떨어지는 것을 봐서는 locality가 일종의 regularization 효과 보다는 모델의 학습을 더 잘 진행하여 표현력을 높일 수 있다고 합니다. 근데 3×3 커널 사이즈에서는 train loss가 크게 더 오르고 test 성능은 좋아졌으니 regularization 효과를 본 것이라고 생각하실 수도 있습니다.

해당 부분에 대해서는 저자가 다른 지표들을 통해서 보았을 때 역시 locality가 regularization이라고 생각하기는 어려우니 그냥 5×5 필터 사이즈가 딱 ViT에 적합한 sweet spot이라고 보는 것이 올바르다 주장합니다.

아무튼 다시 그림4로 돌아와서 그러면 이제 (b)를 보도록 합시다. 4-(b)는 그림3과 동일하게 negative & positive hessian eigenvalue 값들을 계산한 것입니다. 여기서 보시면 MSA연산에 일종의 locality를 부여하게 될 경우 negative hessian value들이 줄어드는 것을 확인하실 수 있습니다.

이러한 실험을 통해 저자는 MSA의 long-range dependency(weak inductive bias) 특성은 negative hessian을 늘려주는 특성이 있으며 곡률의 변화를 줄이는 것에는 딱히 큰 영향을 주지 않는다고 합니다.

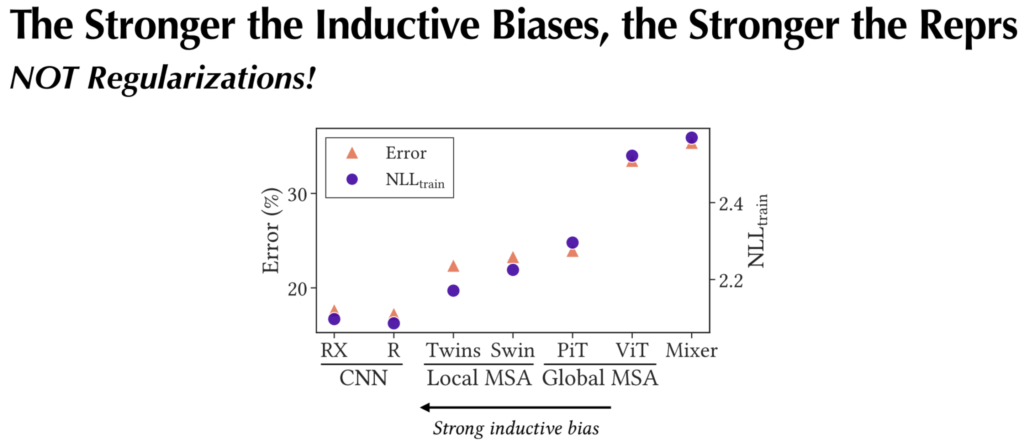
또한 strong inductive bias가 일종의 regularization 효과를 하지 못한다는 것에 대해 추가적인 설명을 더 하자면 그림5에서 CNN과 local MSA를 활용하는 방법론들이 train 대비 test가 더 큰 error 율을 보입니다. 만약 regularization 효과가 있었다면 overfit을 예방하는 효과가 있었을텐데 오히려 Global MSA를 쓴 방법론들이 overfit을 막는듯한 모습을 보여준다는 것이죠.

제가 볼때는 사실 이 주장이 애매한게, train과 test의 성능 갭이 좁은 것만을 보더라도 regularization 효과가 있다는 것이 아닐까..? 라는 생각도 들지만 저자가 말하고자 싶은건 regularization이 주요 쟁점이 아닌, strong inductive bias와 weak inductive bias가 서로 다른 특징들을 가진다는 것을 얘기하고자 하는 것 같습니다.

Q2 : Do MSAs Act Like Convs?

자 그러면 MSA와 Conv는 과연 어떠한 차이가 있을까요? 흔히들 알고 있는 지식으로는, Conv는 data agnostic하지만 channel-specific한 특성을 지니고 있으며, 반대로 MSA연산은 data-specific하지만 channel 축에 대해서는 agnostic한 특성을 가지고 있습니다.

보충 설명하자면 convolution filter는 채널축으로 다 다른 값들을 가지고 있지만 하나의 채널 내에서는 동일한 weight 값으로 연산을 수행하기 때문에 data agnostic, channel-specific이라고 합니다.

이러한 모두가 다 아는 일반적인 특성 말고, 저자는 두 연산법의 새로운 차이에 대하여 주장합니다. 바로 Convolution은 High-Pass Filter인 반면, MSA는 Low-Pass Filter라는 것이죠.

이것에 대한 실험을 진행하고자 저자는 아래 그림6과 같이 Conv와 MSA로 연산이 된 각각의 feature map에 Fourier transform을 수행합니다.

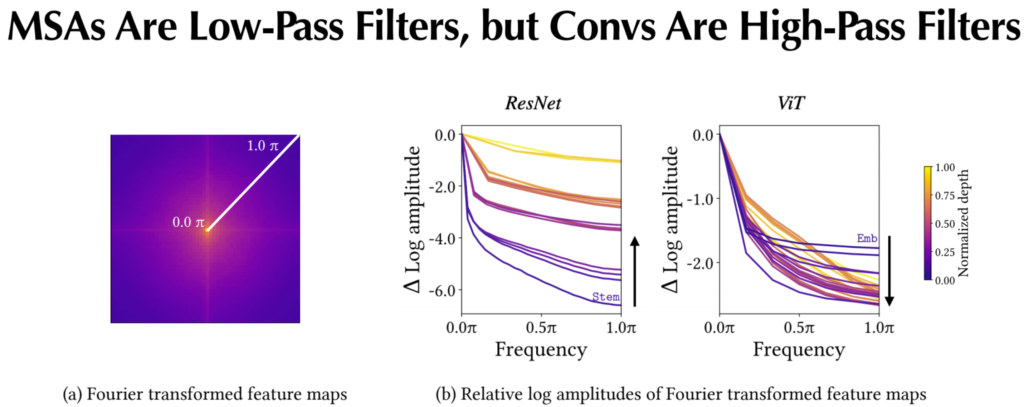
보시면 그림6-(a)는 feature map을 Fourier transformer하였을 때 결과값을 나타내는데, 중앙부에 0.0 파이로 적힌 곳이 low-frequency를 의미하며 가장자리 1.0파이에 해당하는 부분을 high-frequency라고 보시면 될 것 같습니다.

그럼 이제 그림6-(b) 결과를 통해 Conv와 MSA의 특성을 쉽게 확인하실 수 있습니다. 먼저 ResNet의 경우 레이어를 통과하면 통과할 수록 고주파 성분(1.0파이)이 크게 증가하는 것을 확인할 수 있으며, 반대로 ViT의 경우 레이어가 깊어질수록 고주파 성분이 줄어드는 것을 확인하실 수 있습니다.

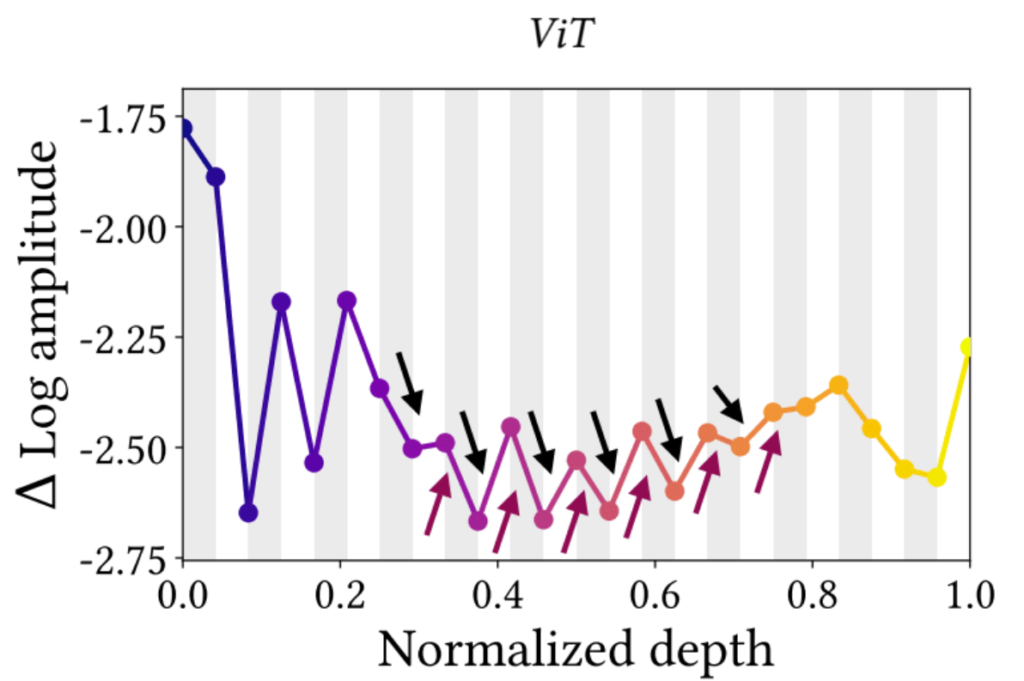
보다 직접적인 비교를 하고자 이번에는 그림7과 같이 ViT 내부에 대해서 고주파 성분의 변화도를 계산하였습니다. y축 값이 작을수록 1.0파이에서 멀어지는 것을 의미하며 이는 고주파 성분이 걸러져서 저주파성분들이 남는 것을 의미합니다. 또한 회색 영역은 MSA를, 흰색 영역은 MLP를 통과한 것을 의미합니다.

자 그러면 지금 전반적인 경향성이 (레이어 초반부를 제외하고) 회색영역(MSA)을 통과하면 1.0파이로부터 멀어지는 즉 고주파 성분이 줄어들며 반대로 MLP 연산을 수행하면 고주파 성분이 늘어나는 것을 확인할 수 있습니다.

자 요약하면 Convolution은 고주파 성분을 통과시키는 high-pass filter 연산이며, MSA는 저주파 성분을 통과시키는 low-pass filter로 볼 수 있다고 하였습니다. 그렇다면 실제 data에 각각 고주파, 저주파 성분의 노이즈를 넣게 될 경우 어떻게 되는 걸까요?

저자는 특정 주파수에 대한 노이즈를 추가하였을 때 CNN과 ViT가 각각 얼마나 성능 감소를 보이는지에 대하여 그림8에 나타내었습니다.

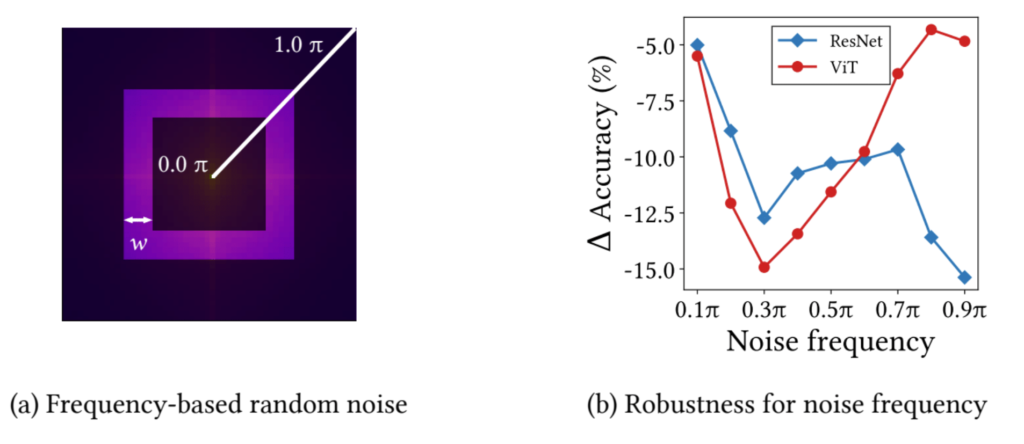
보시면 MSA는 저주파 성분만을 고려하고 고주파 성분은 제거하기 때문에 저주파 성분에 노이즈 들어갈 경우 성능이 크게 감소하며 반대로 고주파 성분에 노이즈가 들어갈 때는 성능 감소 폭이 그리 크지 않은 것을 확인하시 수 있습니다.

반대로 ResNet은 컨볼루션이 high-pass filter이므로 Transformer와 반대의 경향성을 보여주고 있는 모습입니다.

MSA aggregate Feature Maps, but Conv increases the variance.

자 그러면 MSA와 Conv의 차이를 또 다른 관점으로 살펴봅시다. 저자는 ResNet과 ViT에 대하여 각각의 feature map의 variance를 그림9와 같이 표현하였습니다.

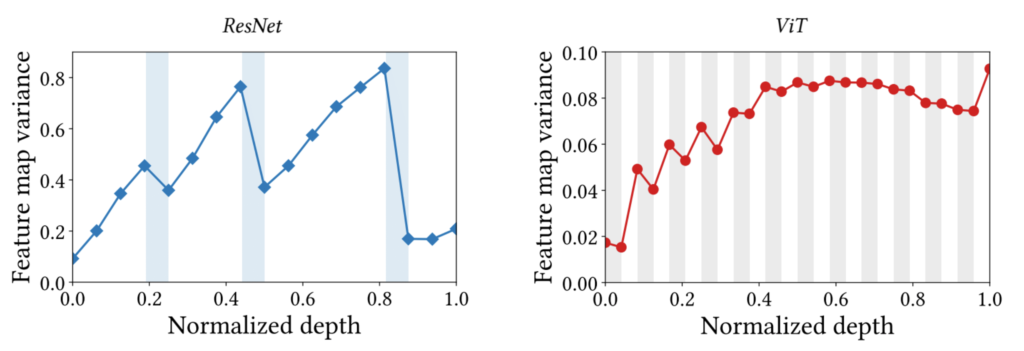
보시면 ResNet의 경우 흰색 영역에서는 variance가 점차 커지다가 하늘색 영역을 통과한 다음에는 variance가 줄어드는 모습을 볼 수 있습니다. ViT도 마찬가지로 하얀색 부분에서는 variance가 증가하는 경향성을 보이며, 회색부분에서는 variance가 감소하는 부분입니다.

여기서 눈치채신 분들은 아시겠지만, 하얀색은 Conv/MLP 연산을 의미합니다. 즉 컨볼루션 연산은 feature의 다양성을 증가시키는 역할을 한다고 볼 수 있는 것이죠.

반면 하늘색과 회색 영역은 각각 pooling과 MSA 연산을 의미합니다. 즉 이들은 컨볼루션 연산으로 다양화된 feature를 모아주는 역할을 수행하는 것이죠. 저자는 이러한 결과를 바탕으로, Conv와 MSA를 동시에 활용하게 될 경우에는 MSA를 Conv 뒷편에 위치하는 것이 바람직하다고 합니다.

Q3 : How Can We Harmonize MSA with Conv?

마지막 질문입니다. 위에 질문들에 대한 대답을 하는 과정에서 저희는 MSA와 Conv의 장단점을 다양한 측면에서 확인할 수 있었습니다.(Hessian, Frequency, Variance etc..)

그리고 이를 통해 Conv와 MSA는 한쪽이 더 우수한 일방적인 관계가 아니라, 서로의 장단점이 명확한 상호보완적인 관계라는 것을 알 수 있게 되었죠. 그렇다면 MSA와 Conv를 어떤식으로 활용하면 좋을까요?

일단 저자는 CNN과 Transformer들이 모두 multi-stage를 가지는 것에 대하여 집중합니다.

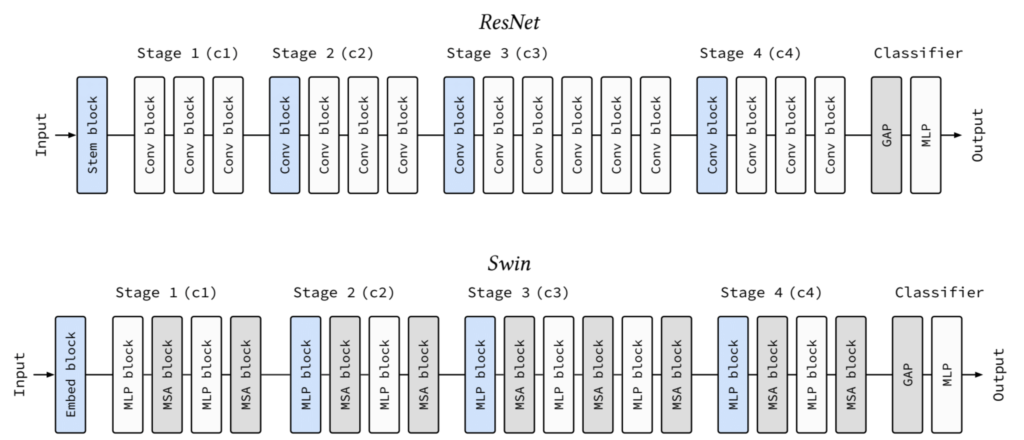
그림10은 ResNet과 Swin Transformer의 모형도를 나타낸 것인데, 이 둘은 동일하게 4개의 스테이지로 나뉘어져 있으며, 각 스테이지로 넘어갈 때마다 해상도가 2배씩 줄어드는 것을 확인하시 수 있습니다.

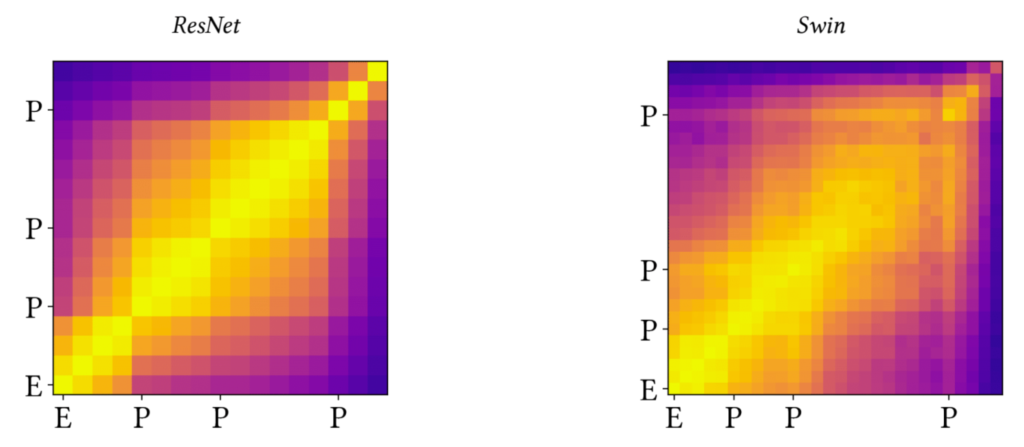
그리고 저자는 각 스테이지별로 featuremap의 유사도를 그림11과 같이 계산하였습니다. 그 결과 동일한 stage 내부의 feature map들은 노란색으로 활성화되어 유사도가 깊은 것을 확인할 수 있으며, 서로 다른 스테이지 끼리는 유사도가 그리 높지 않아 결과적으로 각 스테이지별로 노랗게 활성화된 박스 형태를 띄는 것을 볼 수 있습니다.

이를 통해 저자는 하나의 전체 네트워크는 서로 다른 작은 뉴럴네트워크들이 Sequence하게 이어진 multi-stage network라는 판단을 하게 됩니다.

이와 별개로 저자는 이번엔 Lesion Study를 통해 MSA와 Conv의 역할을 비교합니다. Lesion Study란 이미 학습된 모델을 가지고 특정 레이어나 모듈을 제거하였을 때 모델 성능이 얼만큼 감소하는지를 판단하는 것 입니다.

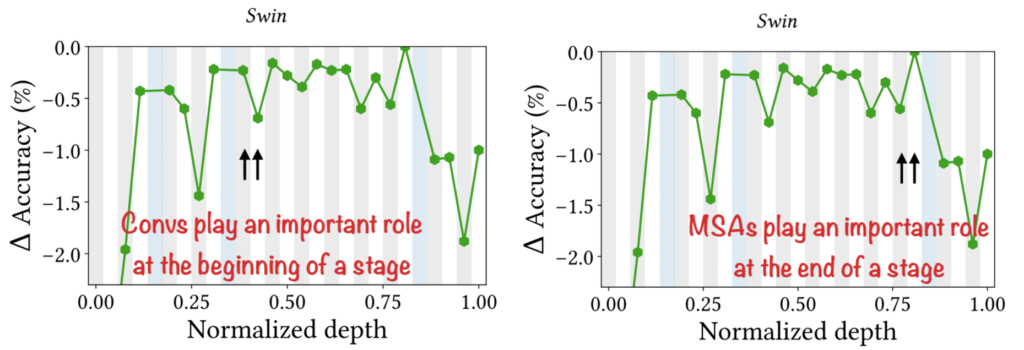
그림12는 모두 Swin Transformer에 대하여 동일한 Lesion Study 결과를 나타낸 것입니다. 그러니 한쪽만 보셔도 상관 없는데, 먼저 Swin Transformer의 경우 중간 stage에서는 MSA보다는 MLP(Conv) 부분을 제거하였을 때 더큰 성능 감소를 보여주고 있습니다.

반면 완전 뒤쪽 stage에서는, MLP보다는 MSA 부분을 제거하게 될 경우 꽤나 큰 폭의 성능 감소를 보여주고 있음을 확인하실 수 있습니다. 즉 후반 stage에서는 MSA가 더 중요한 역할을 수행한다 라는 것을 의미합니다.

저자는 이러한 실험들을 다 종합하였을 때 아래와 같은 결론을 낼 수 있었다고 합니다.

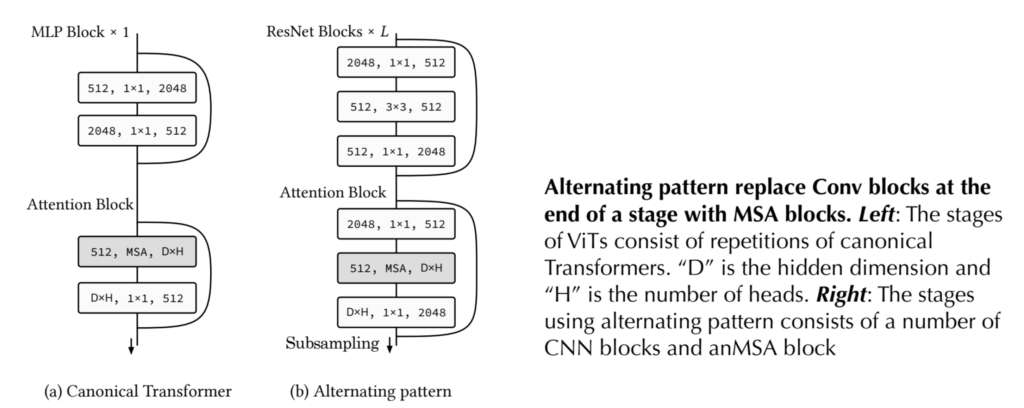
기존의 ViT는 MSA – MLP – MSA – MLP 등 번갈아가면서 연산을 수행하였습니다. 하지만 저자는 그러한 방식이 아닌, 먼저 Conv으로만 이루어진 블록의 연산을 쭉 수행한 뒤, 현재 stage가 끝난 후 다음 스테이지로 넘어가기 전에 pooling하듯이, MSA를 추가하는 방향을 제안합니다.

그리고 이러한 Conv block과 하나의 MSA를 한 스테이지로 보고 multi-stage로 모델을 구성하는 것이 최종 네트워크의 방향성입니다.

정리하자면 다음과 같은 규칙을 통해 저자가 말하는 새로운 하모니 구조를 생성할 수 있습니다.

1. Baseline CNN model(e.g ResNet)의 제일 마지막에 Conv Block을 MSA Block이 뒤따라오는 Conv Block으로 대체한다.
2. 성능이 계속해서 개선될 때까지, 단순한 Conv Block을 MSA Block이 뒤따라오는 Conv Block으로 대체한다.
3. 만약 성능이 개선되지 않았을 경우, 해당 스테이지에서는 더이상의 1~2번 규칙을 적용하지 않으며 다음 스테이지에서 다시 1~2번 규칙을 적용한다.

위의 규칙을 글로만 보면 이해하기 어려우실까봐 그림으로 살펴보도록 하겠습니다.

보시면 먼저 맨 마지막 스테이지부터 차례차례 (Conv block – MSA Block)을 붙여나갑니다. c4의 경우 MSA block을 계속 추가할수록 성능이 개선되지만, c3의 경우 2개 이상의 MSA block이 들어가는 순간 성능이 감소되게 됩니다.

이 경우에는 더이상 MSA를 c3에 추가하지는 않지만, c2의 마지막에 다시 추가하게 됩니다. 이때 성능이 크게 향상되는 것을 위의 Accuracy를 통해 확인하실 수 있습니다. 그리고 c2에 2개 이상의 MSA를 놓게 되면 다시 성능이 감소하니, 제거해주는 모습이며 마지막 c1의 경우 MSA를 하나만 추가해도 성능이 감소되므로, 최종적인 모델은 그림15와 같이 이루어지게 됩니다.

Experiments

자 그러면 거의 다 마쳤습니다. 이제 저자가 제안하는 새로운 구조는 어떠한 이점을 보이는지를 살펴봅시다.

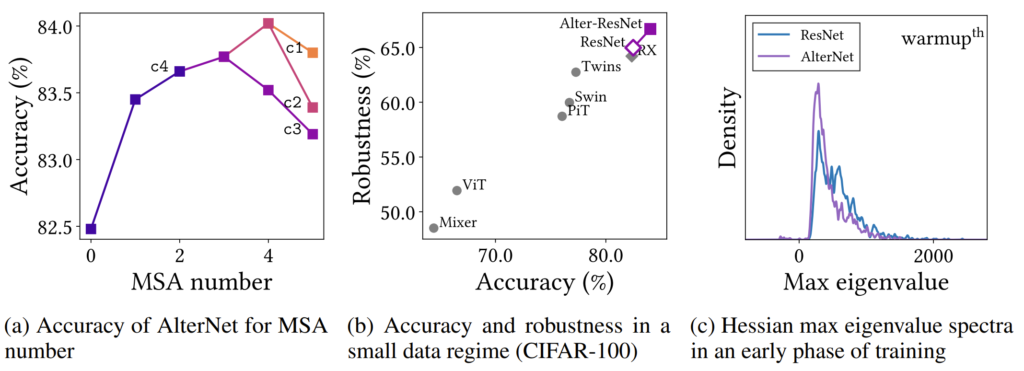
위의 결과를 보면 먼저 (a)는 그림14에서의 결과라고 보시면 될 것 같습니다. (b)의 경우에는 CIFAR-100과 같이 데이터가 많지 않은 모델에 대하여 정확도와 robustness를 측정한 것으로 보시면 됩니다. 참고로 robustness는 CIFAR-100의 평균 정확도라고 합니다.

아무튼 기존의 ViT를 대표적으로 Data hungry 특성이 강한 transformer 모델은 최소한 ImageNet-1K 수준의 방대한 데이터가 필요하기에, 데이터 수가 작은 CIFAR-100에서는 CNN 기반 방법론인 ResNet과 RX(ResNeXt)보다 성능이 좋지 못한 것을 확인하실 수 있습니다.

하지만 저자가 제안하는 Alter-ResNet의 경우 Transformer처럼 MSA 연산이 들어갔음에도 불구하고 CNN 모델들보다 더 좋은 성능을 보여주고 있습니다. 즉 Transformer의 장점은 크게 얻으면서, 단점인 data hungry 특성은 잘 해결했다는 점이죠.

또한 (c) 결과를 살펴보시면, positive max hessian eigenvalue 값들이 상대적으로 작아지는 현상을 볼 수 있으며, negative hessian eigenvalue 역시 줄어들어 saddle point가 크게 줄어든 모습을 확인하실 수 있습니다.

결론

해당 논문은 조원 연구원님이 공유해주신 덕분에 알게 되었는데, 기존의 ViT 관련했던 문제점들이 왜 말썽이었는지에 대하여 새로운 측면으로 확인할 수 있어서 정말 좋았습니다. 참고로 저자분이 연세대에서 박사 과정을 하시는 분께서 작성한 논문이라 직접 저자분이 한국말로 세미나 해주신 영상도 존재합니다.

Transformer에 관심 있으신 분들 또는 컨볼루션의 특징에 대해서 공부해보실 분들은 해당 논문 읽는 것을 강추합니다. 그리고 논문의 appendix가 엄청난 고봉밥을 자랑하니 시간 및 관심 있으신 분들은 한번쯤 읽어보시는 것도 좋겠네요ㅎㅎ..