이번 논문은 Normalizing-flow를 이용한 Super resolution 방법론 입니다. 제가 요즘 Normalizing-flow(NF)에 많은 관심을 가지고 있다는 것을 연구실 내 몇몇 분들은 알고 있으실 겁니다. 근데 어쩌다가 관심이 생긴 것인지는 다들 모르고 계실 거라 생각하는데요. 오늘 리뷰 논문이 이에 대한 답변 중 하나이며, 다른 연구원들도 관심을 가지게 될 계기가 될 거라고 생각합니다.
Intro
cGAN vs SRFlow

위에 있는 GIF를 보시면 cGAN과 리뷰 방법론인 SRFlow을 “cGAN is deterministic.”, “SRFlow is Stochastic“라고 설명합니다.
조금 쉽게 풀어서 설명하자면 cGAN은 입력값에 대응되는 출력값이 결정된 상태인 반면에 SRFlow는 입력값에 대응되는 값이 단일 값이 아닌 확률 분포를 가진 값을 가진다고 보시면 됩니다. 그런데 사실 값이 명확한 경우가 더 좋은 경우에 해당하지 않나? 란 의문점이 들 수 있습니다. 이런 의문점에도 불구하고 자신의 방법론이 “Stochastic” 하다는 주장을 왜 하는 지에 대한 궁금증을 해결하기 위해서는 GAN의 한계에 대해 알아야 합니다.

GAN에는 풀어야 나가야 할 여러 한계가 있지만 가장 대표적인 한계로 알려진 Mode Collapse 가 있습니다. 이는 생성자와 판별자 간 균형이 무너져 한 분포에만 치우지는 현상을 의미합니다. 이러한 문제는 생각보다 흔하게 발생합니다. 제 경험을 예를 들자면 중기청 과제에서 작물 질병에 대한 Image trnaslation을 진행하면서 나타났습니다. 변화하길 희망하는 작물 상태, 즉 개별적인 condition을 주었는데도 불구하고 작물 질병이 고정된 형태와 위치로 영상이 변화하는 현상이 발생했습니다. 이렇게 한 쪽에 치우치는 경우를 Mode Collapse라고 부릅니다.
이런 현상은 GAN의 목적인 판별자를 속이는 것이기에 발생하는 문제라고 볼 수 있습니다. 방금 예시를 든 Mode Collapse이 발생한 작물 질병에 대한 Image trnaslation 결과값들은 사람이 봐도 명확한 형태와 위치에 질병이 발생한 것을 볼 수 있었습니다. 반면에 condition으로 준 실제 작물 질병 영상은 비교적 명확하지 않은 경우가 많습니다. 질병이 옅은 케이스가 들어온 경우, 판별자는 생성자가 생성한 영상이 상대적으로 더욱 명확하기 때문에 진짜라고 판별하게 됩니다. 이러한 행위가 반복되면서 생성자는 판별자가 잘 속았던 생성 영상을 생성하는 방향으로 학습이 되며 Mode Collapse가 발생하게 됩니다.
앞서 설명한 내용을 통해 GAN은 condition으로 입력된 임의 값을 무시하고 생성 영상을 생성하는 케이스를 보았습니다. 이를 통해 GAN은 영상 대 영상, deterministic 특성을 강하게 가진 것을 알 수 있으며, 이로 인해 문제가 발생할 수 있다는 것을 볼 수 있습니다.
반면에 SRFlow는 가역적인 transformation으로 구성된 NF를 기반임으로 영상 대 영상이 아닌 데이터 분포를 명시적으로 학습이 가능합니다. 또한 제안한 Conditional Affine Coupling을 통해 Low resolution image(LR)을 condition으로 injection 함으로써 LR의 정보를 유지한 채 학습 및 추론이 가능해집니다.
Super resolution

Super resolution(SR)은 저해상도의 영상을 고해상도로 복원하는 태스크에 해당합니다. 해당 태스크는 영상 압축, 영상 복원 등 굉장히 많은 태스크에서 사용할 수 있으며, 컴퓨터 비전 분야에서는 전처리로써 사용이 가능하기에 무궁무진한 잠재력을 가진 태스크에 해당합니다. 그렇기에 많은 연구들이 진행되고 있으나, 꽤나 어려움을 가지고 있는 것이 사실입니다. 가장 대표적인 문제로 ill-pose problem이 있습니다. 위의 LR에 해당하는 왼쪽과 High resolution(HR)에 해당하는 오른쪽 영상을 비교해보면, 압축 손실로 인해 눈동자 모양, 털의 디테일, 수염 등 상당한 부분의 정보가 손실된 것을 볼 수 있습니다. 이러한 케이스에서 LR을 복원할 경우, 정보의 모호성(e.g.고양이의 수염 갯수, 위치 형태, 동공의 위치 등)으로 인해 단일 HR 영상이 아닌 여러 경우의 HR 영상이 존재한다는 문제가 있습니다. 하지만 기술의 한계로 현재 대부분의 연구들은 단일 고해상도 영상만을 예측하는 Single Image Super Resolution 에 대한 문제만 해결하는 추세입니다. 이런 한계는 라벨을 이용하는 지도 학습 기반의 방법의 특성(deterministic)으로 인한 한계로 볼 수 있습니다.
반면에 SRFlow는 라벨인 아닌 데이터 분포만을 이용하여 학습을 진행합니다. 이러한 특성으로 인해 유연한 표현이 가능해져 다중 고해상도 영상을 예측, 즉 Multi Image Super Resolution이 가능하다는 장점이 있습니다.
Normalizing flow
![slow paper] Glow: Generative Flow with Invertible 1x1 Convolutions | by Sunwoo Park | Medium](https://miro.medium.com/max/1838/1*4F-PlK3BotB-syKvcZZd-w.png)
NF는 Yoshua Bengio 그룹에서 발표한 NICE 을 통해 처음 머신 러닝에 적용되었습니다. NF의 기본적인 개념은 복잡한 분포를 만들기 위해 단순한 분포 p(z)에 순차적으로 f_i를 통해 복잡한 분포 p(x)를 만들자는 컨셉에서 시작합니다. 아주 단순하지만 명확한 방법이죠. 그럼 여기서 f를 어떻게 최적화 시킬 수 있을까요?
생각보다 의외의 곳에서 정답을 찾을 수 있습니다. 확률과 통계를 배우신 분들이라면 확률 변수 변환이라는 공식을 기억하실 겁니다. 아래의 수식은 다변수 확률 변수 변환에 해당합니다.

즉, f_i들에 대한 자코비안 행렬만 구할 수 있다면, 해당 문제를 해결할 수 있게 됩니다. 최종적으로 log 스케일이 추가된 아래 수식을 통해 알고 싶은 data space에서의 likelihood p(x)에 대해 직접적으로 Negative Log Likelihood를 푸는 문제로 단순화됩니다.
그럼 다시 의문점이 이렇게 좋은 알고리즘을 두고, 사용하지 않는 것일까요?
그건 바로 아래에서 이야기할 두 가지 조건으로 인하여 발생합니다. 먼저 기반이 되는 수식, 확률 변수 변환 공식이 적용되기 위해서는 1대1 대응 함수(전단사 함수), 즉 f가 가역성을 가져야만 합니다. 두번째, 자코비안 행렬의 계산량이 다루기 쉬워야만 합니다.
이러한 조건들로 인해 실제로 적용하기 어려움이 발생합니다. 하지만 이런한 한계에도 불구하고 위에서 언급한 NICE는 몇 가지 트릭을 이용하여 앞선 조건들을 만족 시키는 방법을 제안합니다.
NICE에서는 아래와 같은 형태를 가진 coupling layer라는 방법을 제안합니다.
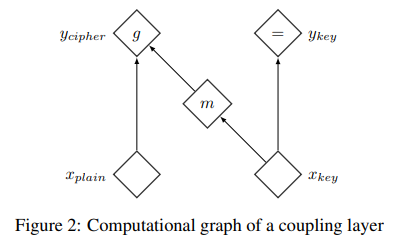
coupling layer는 x를 y로 추론하며 가역성을 가지고 자코비안 행렬의 연산을 쉽게 하기 위해 위와 같은 구조를 취합니다. 수식화하면 아래와 같습니다.
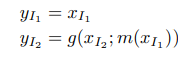
최종적인 y는 concat(y1, y2)로 얻어집니다. 여기서 m은 간단한 layer로 보시면 됩니다. m은 어떤 layer여도 상관 없습니다. (이러한 이유는 이어지는 설명을 통해 이해할 수 있습니다.) 단, g는 가역성을 고려해야하는데, 저자는 간단하게 취하기 위해서 +를 사용했습니다. (이러한 방법은 이후 flow 기반의 방법론에서도 그대로 수용합니다.) 이에 대한 역 함수에 대한 수식은 아래와 같습니다.
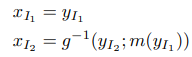
위에서 언급한 바와 같이 g는 +이기에, 이에 대한 역은 -로 보시면 됩니다. 이를 통해 첫번쨰 조건인 가역성 문제를 해결합니다.
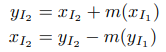
남은 두번째 조건인 자코비안의 쉬운 연산은 앞선 coupling layer를 통해 해결합니다. 그에 대한 수식은 아래와 같습니다.
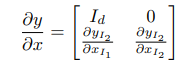
개인적으로 가장 재밌는 트릭이 해당 부분으로 생각합니다. y1=x1 이란 트릭이 행렬의 1열을 I와 0으로 만드는 건 정말 기발한 것 같습니다. 이를 통해 자코비안 행렬은 삼각 행렬을 구조를 가짐으로써, 우리는 최종적으로 diagonal을 이용하여 연산에 필요한 행렬식을 얻을 수 있게 됩니다. 여기서 한 가지, 해당 트릭의 놀라움은 dy2/dx1에 있습니다. 앞선 언급한 바와 같이 m은 아무 layer나 상관 없다고 했습니다. 해당 트릭에서 자코비안 행렬이 삼각 행렬이 됨으로써 대각 행렬의 diagonal만 필요하게 되어 dy2/dx1이 어떤 값이 들어와도 상관 없게 됩니다.
최종적으로 위에 정의된 log 텀을 통해 NLL loss로 최적화가 이뤄집니다.
SRFlow는 NF를 기반으로 구성된 모델을 제안합니다. 이를 통해 명시적으로 데이터 분포를 학습함으로써, ill-pose problem을 해결하고 cGAN이 겪고 있는 Mode collapse 문제를 해결할 수 있게 됩니다.
Method
전반적으로 어려운 이야기를 intro에서 다 풀었기 때문에 여기부터는 비교적 쉽게 이해 할 수 있습니다. 사실 저자가 제안한 방식은 flow 기반 생산자 모델로 성공한 Glow에 LR의 feature를 injection하는 것 이외에는 대부분 계승하였습니다. 그렇기에 Glow에 대해서는 다음 리뷰에서 자세히 다루고 해당 리뷰에서는 추가된 점만 설명하도록 하겠습니다. 전반적인 흐름은 위의 내용으로도 충분히 이해 가능합니다.
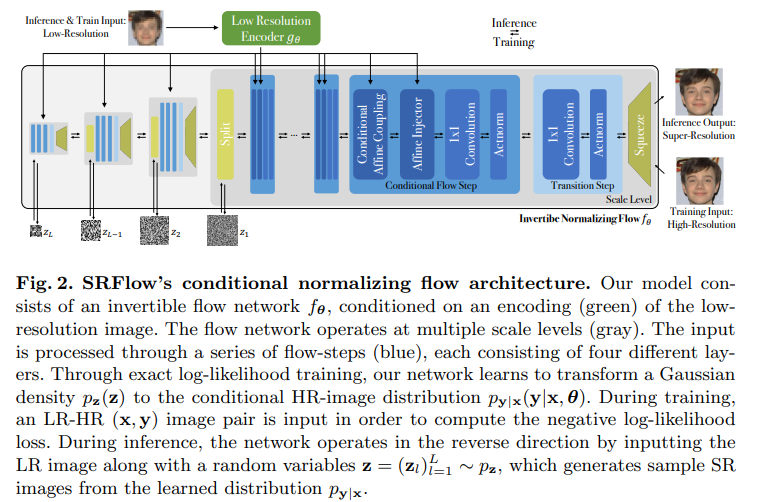
Conditional Flow Layer
Conditional Affine Coupling
저자는 LR의 정보를 효과적으로 전달하기 위해, low resolution image encoding u = g(x)를 통해 condition vector를 생성합니다. 그 후, 제안하는 Affine Injector를 통해 효율적으로 생성 영상을 LR에 해당하는 형태로 유도합니다.
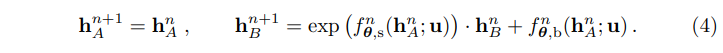
+ 전반적으로 NICE와 유사한 형태를 가지고 있으나, 수식 4의 오른쪽 값이 처음 보는 형태라 의아하실 수 있습니다. 해당 수식의 형태는 Glow에서 제안한 affine coupling 기법으로 기존에 단순히 덧셈만한 NICE에서 스케일링을 담당하는 f_s와 bias를 담당하는 f_b를 추가하여 affine 측면에서 고려한 연산으로 보시면 되며, 저자는 여기다가 LR에 대한 condition vector를 추가하여 예측하는 구나 하시면 됩니다.
Invertible 1 × 1 Convolution
해당 모듈도 Glow에서 제안한 모듈로 추후 자세히 다루도록 하겠습니다. 여기서는 단순하게 x 값을 적응적으로 x를 나누기 위해 사용되었다로 이해하시면 됩니다.
Actnorm
해당 모듈 또한 Glow에서 제안된 방법론으로 적은 Batch로도 Batch normalization의 효과를 얻기 위해 제안한 방법론 입니다. 해당 내용 또한 추후 리뷰에서 자세히 다루도록 하겠습니다.
+ 사실 y = s * x + b 형태를 가진 간단한 수식이긴 합니다만 flow 기반 모델에서는 가역성과 자코비안을 다뤄야 의미가 있기에 자세한 설명은 하지 않도록 하겠습니다.
Squeeze
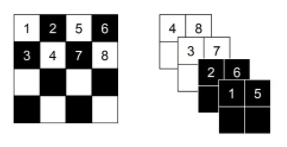
해당 모듈 또한 Glow에서 사용된 방법으로 flow의 특성상 입력값을 반으로 나눠야 합니다. 3차원을 가진 RGB를 고려하여 효과적으로 나누고, 먼거리에 있는 정보들을 수용하기 위한 기법으로 위의 그림과 같이 정보를 압축합니다.
Affine Injector
해당 모듈은 제안한 방법으로 Conditional Affine Coupling과의 차이는 LR에 대한 condition vector u만을 이용하여 직접적으로 정보를 주입합니다.
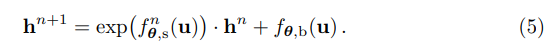
Experiment
저자는 해당 방법론의 Stochastic 한 특성을 보여주기 위해 다양한 실험을 진행하였습니다.
Image Content Transfer

Image Restoration
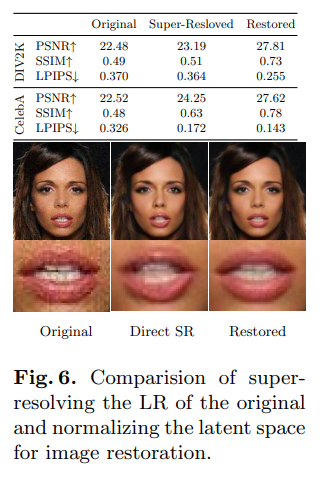
Face Super-Resolution

General Super-Resolution

Ablative Study

============================================================
무엇보다 해당 방법론은 처음으로 conditional NF를 제안한 점과 MISR임에도 불구하고 SR에서 SOTA를 달성한 것에 있어 큰 contribution 주었다고 생각합니다.
그리고 현재 트렌드를 따라가기 위해서는 지도 학습을 벗어나야만 한다고 생각합니다. 저는 이를 위한 지평으로 데이터 분포로만 학습하는 생성 모델 NF이 매우 적절하다고 생각하고 있습니다. 해당 리뷰를 읽은 다른 연구원들의 생각은 어떤지 궁금하네요.
리뷰 잘 읽었습니다. GLow에 대한 리뷰가 벌써부터 기대가 되네요.
Flow의 이점에 대해서도 이번 기회에 잘 알게 되어서 꽤나 만족스러웠습니다.
리뷰 중간에 수식 설명하는 부분이 중간중간 이해가 안가는 부분들이 존재하는데, 혹시 수식 관련 공부하실 때 참고하셨던 사이트나 자료같은 것이 있으신가요? 요번 기회에 Flow에 대해서도 한번 공부해보고자 하는데, Flow에 대하여 공부하실 때 참고하셨던 좋은 정보들이 있으시다면 공유해주시면 감사하겠습니다.
NF을 이해하는데에 있어 기초적인 지식을 얻고 싶으시다면, 이변 확률 변수의 변환을 먼저 보신 다음에 다변수 확률 변수 변환과 Jacobian matrix를 공부하시면 좋습니다. 확률로만 접근해서 어려우시다면 기하학 측면에서의 접근법도 같이 보신다면 이해하는데에 도움이 될겁니다.
(위의 공식들은 교과서에서 다루는 내용으로 블로그에 검색하시면 충분히 많은 내용들을 볼 수 있습니다)
추가로 NF와 flow model에 대해 잘설명한 추천 동영상[1]도 같이 첨부하였으니 공부하시는데에 있어 도움이 되었으면 합니다.
++ 혹시 NICE 쪽에서 설명한 트릭 중 삼각 행렬과 자코비안 행렬에 대한 내용이 이해가 안가시는 거라면 금일 있을 세미나에서 다룰 예정이니 참고하시길 바랍니다.
[1] https://www.youtube.com/watch?v=CGzDh338BUs
감사링 bb