[arXiv 2019] Diverse mini-batch Active Learning

저는 이번에 다시 Active Learning 관련 논문을 들고왔습니다.

Active Learing?

Active Learning (이하 AL)을 쉽게 말하자면 오라클(인간 어노테이터)가 동일한 라벨링을 하더라도 더 효과적인(성능이 오르는) 데이터를 고르는 방법이라고 할 수 있습니다. 다시 말해 AL은 Unlabeled Data에서 사람이 반드시 라벨링을 해야하는 데이터는 무엇일까라는 관점으로 문제를 바라봅니다.

Semi-Supervised Learning 과 차이점?

반면에 Semi-Supervised Learning은 Labeled Data를 이용하여 어떻게 Unlabeled Data 를 라벨링할 수 있는지에 대한 관점으로 문제를 바라봅니다. 다시 말해 각 태스크는 Unlabeled Data를 어떻게 처리할 지에 방향이 다르다고 하면 이해가 수월할 것 같네요.

그렇다면 왜 이 논문을 리뷰하지?

“라벨링할 데이터 선정” 하는 방식에 대하여 현재 AL 안에서도 다양한 방법으로 연구되고 있는데요. 그 중 대표적인 방법이 Pool-Based Sampling 방식으로 순서는 다음과 같습니다.: 1) Labeled Data로 모델 학습 2) 라벨링할 데이터 선정 후 오라클에게 전달 및 라벨링 3) 라벨링 데이터를 기존 Labeled Data와 합쳐 다시 모델학습

기존 연구들은 2)번 단계에서 오라클에게 전달할 때 데이터에서 개별 인스턴스의 정보량을 파악 후, 각 인스턴스를 쿼리(라벨링 요청)하는 방식이 지배적이었습니다. 그러나 최근 모델은 배치 단위로 학습하는 데다가, 개별 데이터를 사람이 하나씩 라벨링하는 것은 비효율적이라는 문제가 있습니다.

따라서, 배치 방식으로 쿼리를 보내는 방법론인 batch-mode active learning 이 제안이 되었습니다. 제가 이전에 리뷰한 Active learning for convolutional neural networks: A core-set approach 역시 배치 기반으로 쿼리를 보내는 방식을 취합니다. 그러나 해당 논문을 온전히 이해하는 데에는 제가 아직 부족함이 많은 것 같아서, 비슷한 방법론을 제안한 Amazon Research의 “Diverse mini-batch Active Learning” 에 대해 읽어보았습니다.

이제 논문 리뷰를 시작해보도록 하겠습니다.

---

[arXiv 2019] Diverse mini-batch Active Learning

Introduction

제가 이전 리뷰(A core-set approach) 에서 서술한 Divesity, 그리고 Informative-based 방법론들에 대해 언급합니다.

- Informative: 쿼리하는 인스턴스는 정보력을 가져야 한다.
- Diversity: 쿼리하는 인스턴스는 서로 분별된 정보를 가지고 있어야 한다.

Informative (정보력을 갖춘) 데이터라고 한다면, 해당 데이터로 성능이 상승할 수 있는 데이터라고 할 수 있습니다. 이전 리뷰에서는 Uncertainty라고도 표현하였습니다.

사실 AL에서 데이터를 선정하는 방식을 직관적으로 생각하면 정보력이 높은 Top-K를 쿼리하는 방법이 있는데요. 그러나 이 방법의 단점은 “Redundancy(중복)” 이라는 문제점이 존재합니다. 대게 정보력이 많은 데이터만을 선정하게 되면 전체 분포를 고려하지 않은, 즉 서로 분별되는 정보가 아닌 정보력이 많은 비슷한 인스턴스에 대해서만 쿼리할 수도 있게 되는 거죠.

따라서 본 논문에서는 라벨링을 위한 배치 단위의 샘플을 선정하기 위한 informativeness 와 diversity 를 통합하는 알고리즘을 제안합니다.

그렇다면 어떻게 배치 단위로 인스턴스를 쿼리하고, 어떻게 informativeness와 diversity를 통합하였는지, 그리고 정말로 통합한 것이 맞는지를 리뷰해보도록 하겠습니다.

Method

위의 그림은 k-means algorithm을 대표하는 이미지입니다. 라벨은 알 수 없지만, 데이터들을 input space에 흩뿌린 상태에서 밀집한 것들을 같은 클러스터로 본다라는 아이디어에서 나온 알고리즘입니다. 공식은 아래와 같습니다.

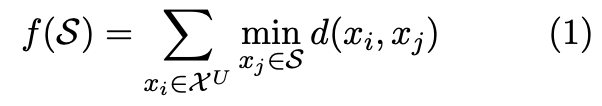
위의 식을 풀어보면, 라벨이 없는 데이터(비지도 학습이기 때문입니다)와 특정 centriod 와의 거리를 최소화하는 centriod 를 반복을 통해 계산하는 작업이 됩니다. j개의 centriod는 j개의 클러스터를 생성하고 새로운 데이터가 들어오면, 각각의 centriod 중 가장 가까운 위치에 있는 클러스터에 속하게 되는 것이죠. 따라서 본 논문은 쿼리하는 j 개의 인스턴스가 각각 다른 클러스터에 속하게끔 하여, diversity를 충족시키게끔 합니다.

정보의 양도 중요하지만, 정보의 다양성도 중요하기 때문에, 이를 각각의 centriod와 얼마나 가까운지까지 고려해 인스턴스의 정보력을 계산하겠다의 맥락이 되는 것입니다. 이러한 아이디어에 따라 아래의 새로운 목적 함수를 제시합니다.

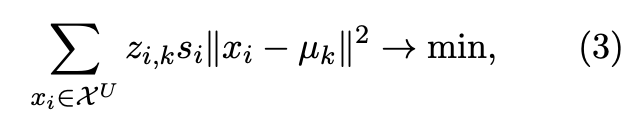
위의 등식에서 z_{i,k} 는 거리를 계산할 때, 데이터들을 해당 클러스터에 속하는 데이터의 거리만 계산할 수 있게끔 하는 [0,1] 두 개의 값을 가지는 값입니다. s_i 는 i 번째 인스턴스의 정보량에 대한 것입니다.

Experiment

논문의 저자는 query strategy에서 Margin Sampling을 사용합니다. 논문 내에서 Least Confidence나 Entropy sampling은 종종 random sampling보다 성능이 낮아, 해당 방법론을 사용했다고 합니다.

쿼리를 하는 인스턴스의 크기 k 에 대해서는 데이터셋 자체의 크기에 따라 다른 값을 적용하였다고 합니다. 전체적으로는 k=100 을 적용했지만, 상대적으로 데이터 크기가 큰 CIFAR-10에 대해서는 1,000을 적용했다고 합니다. 또한, 전체 데이터(U) 에 대해서 k-means 알고리즘을 적용한 것이 아니라, 일부 데이터에 대해서만 클러스터링을 적용하였는데, 그에 대한 크기도 파라미터가 됩니다. 공식은 아래와 같습니다.  βk>k 즉, β는 양수가 되는데, 예를 들어, 10개의 인스턴스를 쿼리하기로 하였고, β를 10으로 설정하였다면, 후보군 데이터셋을 100개로 선정하여, 클러스터링을 한 것이 됩니다.

이는 굉장히 중요한 파라미터로 이 역시 데이터셋의 크기에 따라 적정값이 존재하며, 데이터셋의 크기가 클 수록 큰 β 가 권장된다고 합니다. 또한, 쿼리하는 인스턴스의 갯수 k에도 의존적이라고 합니다. 아래 Section 에 따르면 β=10 이 robust한 성능을 보인다고 합니다

추가적으로 전체 데이터의 60~70 퍼센트의 데이터에 라벨링을 선별적으로 하는 것을 목표로 하였다고 합니다.

Results

해당 논문은 총 4가지 데이터셋에 대해 성능 평가를 보여줬는데요, 그 중 이미지 데이터셋인 MNIST와 CIFAR-10 에 대해서만 아래 첨부하였습니다.

MNIST

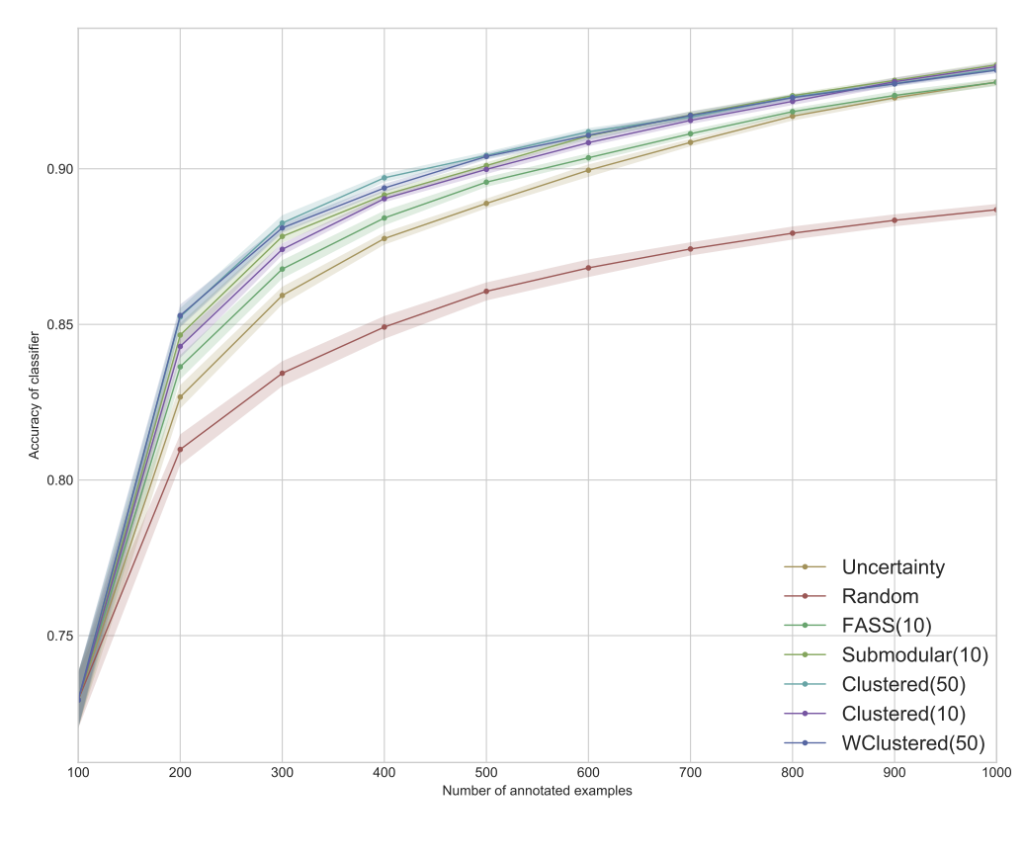
Accuracy on MNIST dataset

MNIST 데이터셋의 결과인 상단 그래프를 통해 먼저, 모든 Diversity-Based 방법이 Uncertainty 샘플링 기반의 방법론보다 우수하다는 것을 확인할 수 있었다고 합니다. 게다가 pre-filtering으로 큰 값을 가지는 β = 50의 Weighted Clustering 방법과 unweighted Clustering 방법 모두 β = 10의 더 작은 pre-filitering으로 Diversity-Based 방법을 뛰어넘으며, 동일한 β 값에 대해 본 논문에서 제안한 방법이 Submodular 뿐만 아니라 FASS보다 뛰어난 것을 확인할 수 있었습니다.

CIFAR-10

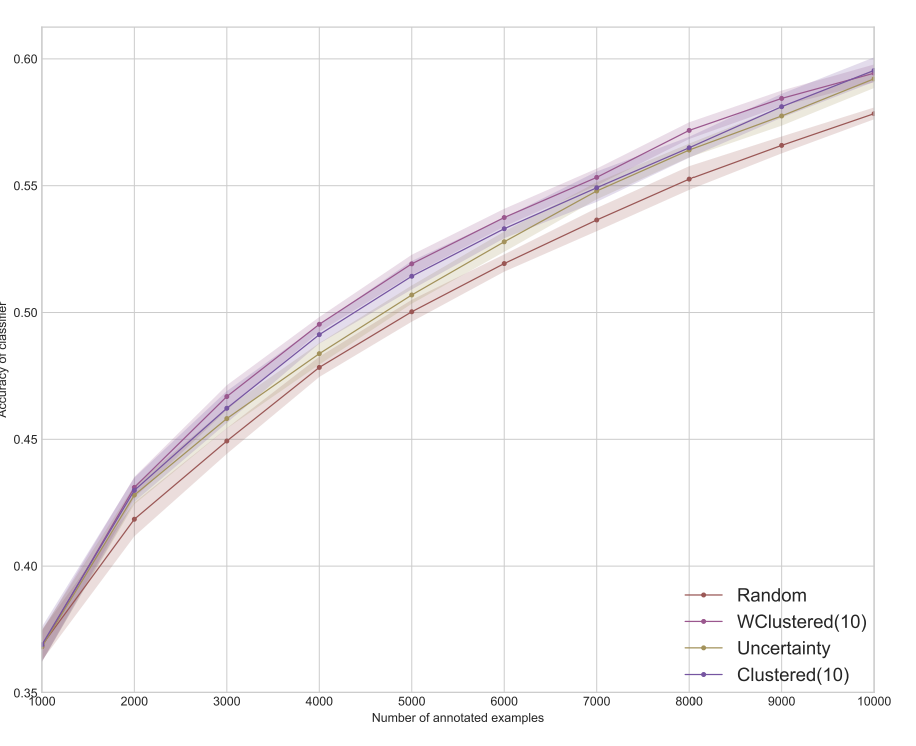
Accuracy on CIFAR-10 dataset

CIFAR-10의 경우 단순한 모델로는 충분한 성능이 나지 않기에 Resnet을 사용하였습니다. 이 때, 파라미터를 학습하기 위해서는 더 많은 데이터가 필요하기 때문에 배치 크기 k = 1,000으로 budget B = 10,000으로 늘려 실험 결과를 리포팅합니다.

상단 그림을 통해 Diversity-Based 방법이 Uncertainty 기반 샘플링보다 성능이 좋고, Weighted Clustering 이 Unweighted Clustering 버전을 능가하는 것을 확인할 수 있습니다.

Discussion

해당 방법론은 이전에 이루어져왔던 submodular function을 통해 diversity를 해결해왔던 논문들과는 달리 k-means algorithm을 통해, diversity를 해결하려 했다는 점에 의의가 있으며, 연산 복잡도 또한, 기존의 지수 복잡도에서 선형 복잡도로 줄여 속도 면에서도 크게 기여했다는 점에 의미가 있을 것 같습니다.