이번 리뷰 논문은 un/self-supervised represetation learning에 관한 내용입니다. 해당 방법론은 아주 간단하고 재밌는 개선된 방법론을 제시합니다. 기존 연구들과 동일하게 Siamese networks를 이용하는 방법을 사용하되, 한쪽에는 stop-gradient를 적용하는 방법을 사용합니다. 또한 Negative sample pair를 사용하지 않습니다. 추가적인 모델 설계와 새로운 개념을 추가하던 이전 방법론과는 다르게 minimalism을 추구하며 개선한 방법론은 현존하는 SOTA 방법론과도 경쟁력을 가진 성능을 보여줍니다.
Intro
우선 이번 리뷰에서 다룰 un/self-supervised represetation learning에 대해 모를 연구원들을 위해 간단하게 설명하고 넘어가고자 합니다. 정말 간단하게 설명하자면, 라벨이 없이 영상만으로 분류 문제를 풀고자 하는 태스크라고 이해하시면 됩니다.
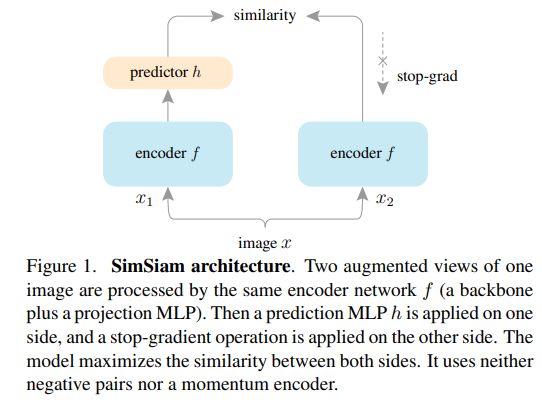
해당 태스크의 연구 흐름은 한 영상으로부터 다양한 augmentation을 가하여 동일한 구조에 파라미터를 공유하는 Siamese Networks에 태워 유사한 예측을 하도록 하여 feature representation에 대한 invariability를 가지도록 학습하는 방법(e.g. SimCLR, SwAV, BYOL…) 이 주를 이루고 있습니다.
기존의 연구들은 몇 가지 한계를 가지고 있었습니다. 4096의 매우 큰 배치 사이즈로 학습을 해야 하며, dissimilarity를 계산하기 위한 negative sample pair가 필요하다는 한계가 있었습니다. 이러한 한계들은 다양한 표현으로 인한 분포를 학습하는 방법들로 일정 학습 정보가 업데이트되면, 이러한 다양한 표현도 상수로 취급되어져 모델의 표현력이 ‘collapsing’된다는 문제가 있습니다.
+ 저자가 언급하는 ‘collapsing’은 feature reprensetaion에 대한 이야기입니다. 특징이 점차 두드러져야만 성능이 개선되지만, 학습이 점차 진행됨에 따라 평준화되는 현상을 의미하는 것으로 해석했습니다. 저자는 평준화되는 현상을 대조되는 특징 값이 상수화되는 현상이 원인이라고 하며, 이에 대한 증명은 실험적인 결과와 개념 증명을 통해 이야기합니다.
저자는 stop-gradient가 ‘collapsing’를 해결하기 위한 방법이라고 주장합니다.
Method

저자가 제안한 방법론은 Fig 1과 Alg 1에서도 확인 가능하듯이 매우 간단한 방법으로 작동합니다.
먼저 영상 x에 서로 다른 augmentaion을 가한 x1 = aug1(x), x2 = aug2(x)을 backbone model f (e.g. ResNet)와 Projection MLP에 태워 임베딩된 벡터 z1, z2를 추출합니다. 그 다음 prediction MLP h에 태워 output vector p1과 p2를 추출합니다. 추출된 2 쌍의 벡터는 아래의 수식 1과 같은 negative consine-similarity D(p{1,2}, z{2,1}) 최소화하도록 합니다.
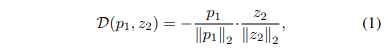
최종적으로 symmetrized loss는 아래의 수식 2와 같습니다.
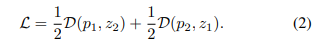
즉, 모든 영상에 대해 각각의 영상로부터 계산된 손실 함수는 -1에 가까워지도록 학습이 진행됩니다. 여기에 추가로 해당 방법론의 핵심인 stop-grad를 추가하면, 아래의 수식 4와 같습니다.
+ 여기서 sotp-grad는 alg 1에서 볼 수 있듯이, torch의 detach와 동일합니다.
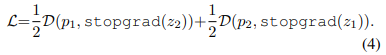
또한 optimizer는 SGD를 사용했으며, 특이하게도 learning rate를 lr x Batchsize/256으로 고정된 값을 사용하며, projection MLP는 2048-d에 3 layers와 BN만 적용하고 ReLU를 제거하였습니다. Prediction MLP은 2개의 layers를 사용하되, output fc에서는 BN과 ReLU를 사용하지 않고, hidden layer에서만 BN을 적용했다고 합니다. output은 둘 다 projection MLP와 동일한 2048-d을 가지며, hidden layer는 512-d를 가집니다.
이러한 구조를 가진 이유는 이후 실험 파트에서 다루도록 하겠습니다.
Experiment
해당 논문은 stop-grad가 어떻게 ‘collpasing’을 예방 했는지에 대해 명백한 증명은 못했다고 이야기합니다. 하지만 실험적인 결과와 개념 증명을 통해서 간접적으로 이를 증명하고자 했습니다. 우선 경험적인 연구인 실험 분석에 대해 다루도록 하겠습니다.
Stop-gradient
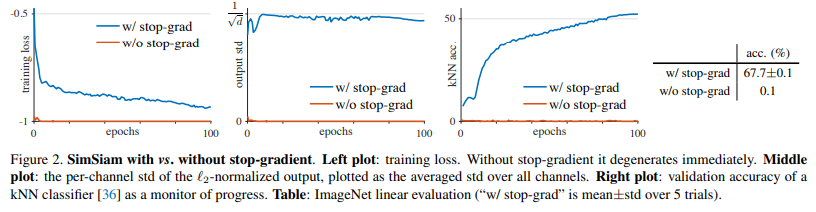
먼저 fig 2의 왼쪽 그래프에서 볼 수 있듯이, 양 쪽에 gradient를 전달할 경우에는 consine-simliarity가 학습 시작과 동시에 -1로 수렴하는 것을 볼 수 있습니다. 이는 대조되는 비교 값이 서로 간에 차별성이 없어진다는 것을 의미합니다. 또한 ‘collapsing’이 output이 상수로 변질된다면, 표준 편차가 ‘0’으로 도달한다는 것을 의미합니다. 이는 출력 값에 대한 표준 편차를 계산한 fig 2 중간 그래프의 빨간 곡선을 통해 대조되는 값이 상수화 된 것을 증명합니다. 마지막으로 fig 2 오른쪽 그래프와 왼쪽 표에서 보이는 바와 같이 output을 이용하여 ImagNet에서의 knn classifier에 대한 결과입니다. stop-grad를 사용한 경우 67.7%의 유의미한 결과를 보이는 반면에 w/o stop-grad는 0.1이라는 처참한 결과를 보여줍니다. 이를 통해 두 대조 값에 대한 차별성이 무너지고, 표현력이 감소한 것을 알 수 있습니다.
Predictor

저자는 Predictor mlp에 대한 3가지 실험을 진행했습니다. 우선 사용하지 않는 경우인 table 1 (a)에서는 0.1이라는 처참한 결과를 보여줌으로써, 해당 모듈이 identity mapping(항등 함수)로써 작동하는 것을 증명합니다. 재밌는 부분이 table 1 (c)로 보입니다. lr를 고정하여 실험을 진행하였을 때, lr이 유동적인 baseline의 성능 67.7%보다 높은 68.1%라는 성능을 달성하였습니다. 이러한 이유로 저자는 gradient가 끝 쪽에 존재하는 해당 모듈까지 충분한 영향력이 발휘하기 전에 lr이 감소한 것이라고 주장합니다.
+ 실제로 그런 것인지는 충분한 분석이 없어 100% 신뢰하기 힘들지만 실제로 다른 분야에도 동일한 결과가 나올 수 있기에 재밌는 분석이라고 생각합니다.
++ table 1 (b)에서는 학습을 진행하지 않고 random init로 초기화하여 실험을 진행하였습니다. 딱히 유의미한 분석은 없었고, 제 생각도 동일하여 아래로 뺐습니다.
Batch Size

Intro에서 다룬 것과 같이 기존 방법론들은 매우 큰 batchsize를 가진 상황에서 충분한 결과를 보여줍니다. 실제로 해당 방법론에서도 Table 2와 같이 Batchsize에 대한 실험을 진행합니다. 저자는 stop-grad를 통해 ‘collapsing’을 예방했기에, 적은 batch에서도 충분한 성능을 보여준다는 것을 Table 2의 실험을 통해 증명하고자 합니다.
+ 이러한 이유는 학습 파라미터가 바꾸기 전에 다양한 표현에 대해 반영하기 위한 것이라고 보고 있습니다. 해당 태스크는 라벨이 없이 학습하기에 다양한 표현에 대한 불변~유사도를 최대한 방영하는 것이 필요한 것으로 보입니다. ~ 확신을 위해서 추후 배치 사이즈가 크다는 방법론의 논문을 읽고 다뤄보도록 하겠습니다.
Batch Normalization

Table 3에서는 제안한 MLP 모듈들에서 BN을 사용한 경우에 대한 실험을 진행하였습니다. 실험적인 결과 적절한 양의 BN은 지도 학습과 동일하게 작동하는 것을 확인하였으나, 이러한 구조적 설계가 collpasing을 예방했다는 것이라고 볼 수 없었습니다.
Similarity Function
저자는 loss의 설계가 collpasing을 예방에 영향을 주었는지에 대한 실험을 진행합니다. 손실함수 중 D(p, z)를 아래의 수식과 같이 변경하여 실험을 진행하였습니다.
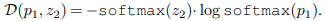
실험적인 결과, 아래의 표와 같이 consine에서는 68.1%, cross-entropy에서는 63.2%라는 성능을 보여주고 있습니다.
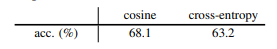
두 손실 함수 모두 유의미한 결과를 보여주고 있으며, consine-similarity가 아닌 다른 손실 함수에서도 효과를 보여주는 것을 의미합니다. 이는 즉, Similarity Function이 collpasing을 예방하는 것에 큰 영향을 주는 것이 아님을 의미합니다.
Symmetrization
마지막으로 실험적인 증명을 위해 저자는 siamese networks의 대칭적인 구조를 변형하여 대칭적인 모델 설계가 collpasing에 영향을 주는 지에 대해 실험하였습니다.

실험적인 결과, 비대칭적인 구조에서도 유의미한 실험 결과를 보여줍니다. 하지만 대칭적인 구조가 성능이 좋은 것을 보았을 때, 대칭적인 구조가 보다 밀도있는 다양한 표현을 보여줌으로써, 성능 향상에 기여했다고 볼 수 있으며, 이는 2장의 영상을 쌍으로 하여 비대칭적인 구조에 입력한 asym. 2x에서의 성능 향상이 앞선 주장을 뒷받침합니다.
Comparisons
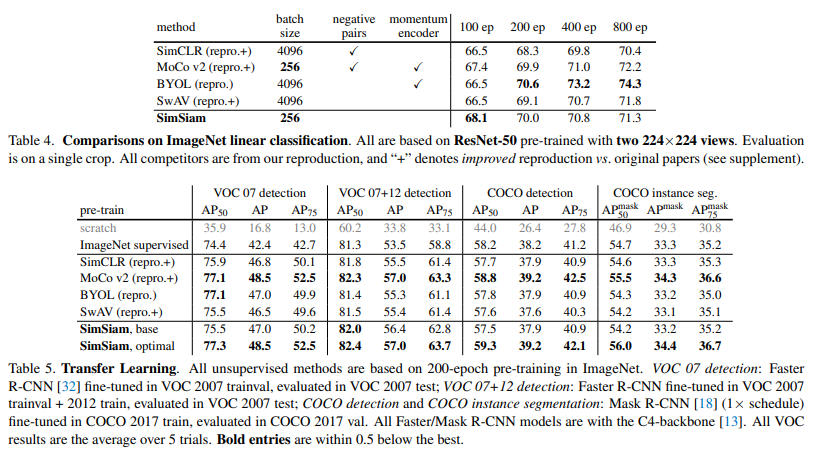
저자는 SOTA를 달성한 방법론들과 ImageNet과 Tansfer learning(detection, segmentation)에서의 성능 비교를 진행하였습니다. Table 4에서 해당 방법론은 상대적으로 작은 Batchsize와 간단한 구조에도 100 epoch에서는 가장 좋은 성능을 보여주고 다른 epoch에서도 경쟁력있는 성능을 보여줍니다. Table 5(공평한 비교를 위해 모든 방법론은 epoch 200에서 실험을 진행)에서는 모든 태스크에서 가장 좋은 성능을 보여주고 있습니다.
+ repro는 실험을 위해 저자가 다시 학습한 경우, +는 성능이 개선된 버전
++ 각 방법론들은 200 epoch보다 더 높은 epoch에서 좋은 성능을 보여줬습니다. 각 방법론이 제시한 epoch에서의 실험도 같이 있었으면 보다 나은 신뢰도를 가졌을 텐데 아쉬운 부분입니다.
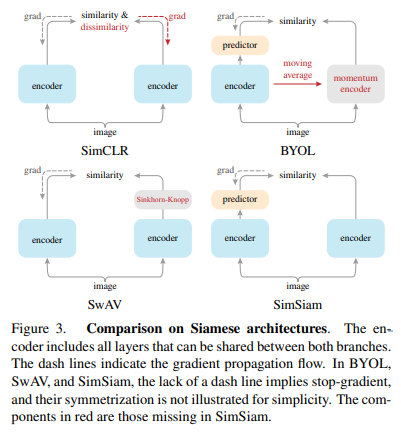
+ Fig 3에서는 SOTA 방법론과의 구조적 차이점을 도식화된 것을 볼 수 있습니다. 빨간색인 부분이 빠진 부분이라고 보시면 됩니다. 위의 방법론에 stop-grad를 추가하여 실험한 내용이 있으나, 각 방법론은 grad를 적용했을 때에 최적화된 설계로 해당 방법론에 대한 이해를 위한 유의미한 결과가 없어 따로 담지는 않았습니다. 궁금하신 분들은 논문을 참고해주세요.
=======================================================
해당 방법론은 얼떨결에 얻어 걸린 방법론이 너무 간단해서 이를 어떻게든 증명하기 위해 고군분투하는 모습이 논문에 담겨져 있었습니다. 하지만 역시는 역시. facebook에서 나온 해당 논문은 이를 과학적으로 유의미한 방향으로 풀어 나갔으며, 더 나아가 collapsing이라는 새로운 문제 정의 까지… 귀납적인 증명은 이런 식으로 하면 되는구나 를 깨닫게 해준 논문이기도 합니다.