이번 논문은 제목과 같이 proxy 기반의 손실 함수를 소개하는 논문입니다. Metric lenaring은 모델로부터 기술된 feature간의 거리를 같은 클래스는 가깝게, 다른 클래스는 멀어지도록 학습을 하는 것이 특징입니다. 이를 통해 feature의 특징이 명확해진다는 장점을 이용하여 유사하거나 특징 묘사가 불분명한 정보 간의 보다 명확한 특징 분류가 가능해집니다. 이러한 특성을 고려하여 이전 리뷰에서 다룬 fine-graied classification에서도 많이 채용하여 사용하기도 합니다. 또는 입력 정보와 유사한 정보들을 검색 해야하는 Retrieval 방법론에서 많이 사용됩니다.
Intro

Metric learning은 모델로부터 기술된 feature 간 의미론적인 거리를 조절하며 학습을 진행합니다. 해당 학습 방법은 크게 2가지로 분류가 됩니다.
우리가 알고 있는 대표적인 Metric learning에서 사용되는 loss로 Triplet loss(Fig 2, (a))가 있습니다. 해당 loss는 비교 기준이 되는 Anchor와 같은 클래스에 해당하는 Positive, 다른 클래스에 해당하는 Negative, 위와 같은 세 개의 데이터가 한 쌍을 이뤄 동일한 모델로 feature를 기술하고 Anchor-Positive 간 거리는 가깝게, Anchor-Negative 간 거리는 멀도록 손실 함수를 설계하여 학습하는 방법론에 해당합니다. 하지만 해당 방법론은 클래스 별 1 vs 1으로 비교한다는 한계를 가지고 있습니다. N-pair loss(Fig 2, (b))는 1 vs 1로 비교하는 Triplet loss의 한계를 극복하고자, Anchor 기준으로 하나의 Anchor-Positive 쌍과 N 개의 Anchor-Negative 쌍을 한번에 계산하는 손실 함수를 설계합니다. Lifted Structure loss(Fig 2, (c))는 N-pair loss와 동일하지만, Anchor-Negative N 개의 쌍 간 어려움 정도를 고려하여 밀어내는 정도를 조절합니다. 위와 같이 두 개 이상의 데이터 간의 관계를 이용하여 데이터와 데이터를 비교하여 보다 세밀한 관계를 학습하는 방법론을 Pair-based loss라고 합니다.
Pair-based loss는 Negtive와 Positive에 대한 지도로 데이터 간 세밀한 관계를 비교하여 학습이 가능합니다. 하지만 M개의 데이터 셋에서 쌍을 생성함으로써, O(M^2), O(M^3) 의 높은 계산 복잡도를 가지게 됩니다. 또한 직접 튜닝을 해야 하며, 이에 따라 오버피팅이 발생한다는 단점이 있습니다.
이런 복잡도 문제를 해결하기 위해서 Proxy-based loss가 제안 되었습니다. Proxy-based loss는 Batch 내에서 proxy를 두어 유사도를 계산하여 샘플링을 진행함으로써 별도의 샘플링을 진행할 필요가 없으며, 또한 직접 pair를 조절하는 것이 아니기에 발생 가능한 outlier와 noise에도 강인한 모습을 보여줍니다. 또한 Batch 자체에서 샘플링을 진행함으로써, 계산 복잡도가 pair-based loss에 비해 낮은 결과를 보여주었습니다. 하지만 직접 계산하는 것이 아닌 데이터 간 유사도를 고려하고, batch 내에서 고려하기 때문에 상대적으로 데이터 간 관계에 대한 고려가 낮아지는 문제가 발생합니다.
저자는 Metric learning를 크게 나누는 2가지 분류의 특성을 합침으로써 한계를 극복할 수 있다고 주장합니다. 저자가 제안하는 Proxy-Anchor loss는 각 proxy를 하나의 anchor로 활용합니다. 그 다음 한 batch 안의 모든 데이터 간 관계를 계산합니다. 이를 통해 별도의 샘플링이 필요 없어지고, nosie와 outliner에도 강인한 특성(proxy-based loss의 장점)을 가지며, 각 데이터에 따라 gradient를 주어줌으로써 데이터 간 관계성을 고려(pair-based loss의 장점)할 수 있다고 주장합니다.
Method
Review of Proxy-NCA Loss
Proxy-based loss는 Proxy Neighbor Component Analusis(NCA) loss에서 처음 제안 되었습니다. Proxy NCA Loss는 각 클래스 별 Proxy를 할당하여 클래스 수와 동일한 proxy를 이용합니다. 아래의 수식과 같이 embedding vector of input x에 같은 클래스인 경우는 positive proxy [latax] p^+ [/latax], 그 외의 클래스는 negative proxy [latax] p^- [/latax]로 두고 input 정보와 proxy 간 거리를 고려하며 학습을 진행합니다.
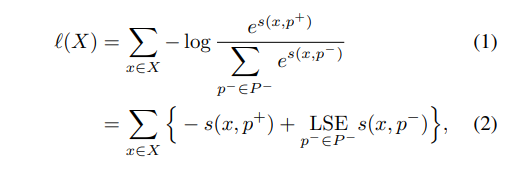
수식 1에서 s는 cosine similarity에 해당하며, 수식 2의 LSE는 Log-Sum-Exp function(+ smoothness를 고려한 max function)에 해당합니다. s(x, p) 관점에서 Proxy NCA loss의 gradient는 아래와 수식과 같습니다.
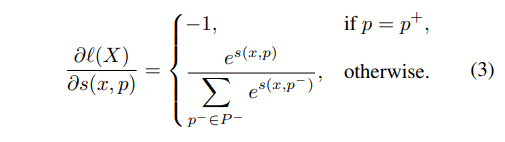
수식 3은 p가 postive일 경우 점점 가까워지도록 고려되고, 그 외의 경우, 유사도에 따라 강도를 조절하며 gradient를 주어줍니다. 즉, 유사도 측면에서 샘플링을 진행함으로써, 별도의 샘플링이 필요 없어집니다. 또한 클래스 수 C를 가진 proxy만 고려하면 됨으로써, 계산 복잡도가 O(MC) 가 됨으로써 pair-based loss보다 효율적으로 빠른 속도로 수렴이 가능해집니다.
하지만 Proxy NCA loss는 입력 데이터와 proxy 간 비교를 함으로써, 데이터-데이터 간 관계성을 고려하지 못하게 된다는 한계를 가집니다.
++ 수식 3을 좀 더 해석하기 위해서는 cosine similiarity에 대한 이해가 있어야합니다. cosine similiarity는 두 벡터가 가까울수록 값이 커집니다. 즉, 유사한 클래스(hard negative)인 경우에는 약하게 밀고, 극단적인 클래스인 경우 더욱 큰 값으로 밀어낸다고 해석할 수 있습니다.
Proxy-Anchor Loss
저자가 제안하는 Proxy-Anchor loss의 주요 아이디어는 각각의 proxy를 anchro로 하여 batch 내의 모든 데이터간 연관성을 계산함으로써 데이터-데이터 연관성(pair-based loss의 장점)을 보고자 합니다(Fig 2, (e)). 제안하는 방법은 Proxy NCA loss와 동일하게 클래스 별 하나의 proxy 할당합니다.
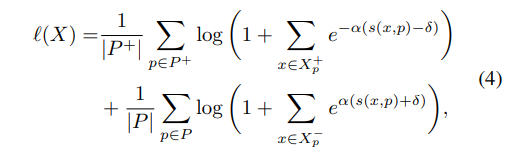
수식 4에서 NCA와 동일하게 모든 proxy P, positive proxies P+에 해당합니다. margin δ>0, scaling factor α>0에 해당하며,임베딩 벡터 집합를 positve vector set Xp+, negative vector set Xp-로 나눠 봅니다. 이를 쉽게 풀면 다음 수식과 같습니다.
++Softplus는 a smooth approximation of ReLU로 보시면 됩니다.
loss의 미분은 아래의 수식과 같습니다.
위의 수식과 Proxy NCA loss와 가장 큰 차이는 batch를 고려하고 Positve proxy 관점에서도 gradient를 부여한다는 점입니다. 먼저 메인이 되는 x에서 batch 내의 x를 X+, X-로 나눠 고려합니다. Proxy 또한 P+, P-로 나눠 메인이 되는 x에서의 proxy의 유사도와 X+와 P+간 정도를 계산함으로써 hard positive를 고려할 수 있게됩니다. Negative 또한 동일하게 작동합니다.
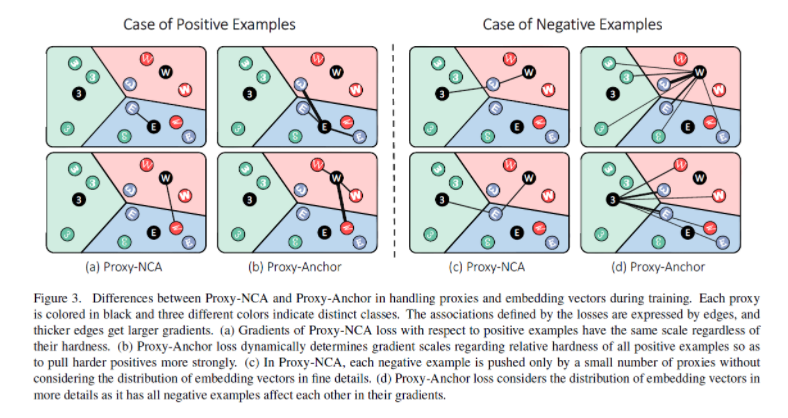
Fig 3과 같이 batch 내의 모든 정보에 대해서 상대적으로 어려운 정보에 더 많은 gradient를 부여함으로써 보다 나은 embedding space를 구성할 수 있게됩니다.
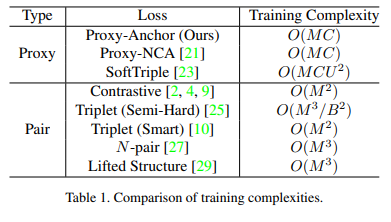
또한 Proxy NCA loss와 동일하게 batch 내 정보와 proxy 간 연산된 정보들을 재사용함으로써 구현이 가능하기에 동일한 O(MC)의 계산 복잡도를 가집니다.
Experiments
실험은 Metric learing에서 많이 사용되는 CUB-200-2011, Cars-196, SOP, In-Shop 위의 4개의 데이터 셋에서 진행되었습니다. 또한 이전 연구에서와 동일하게 Inception 모델에서 사용하였다고 합니다. (++ α=32, δ=10−1)
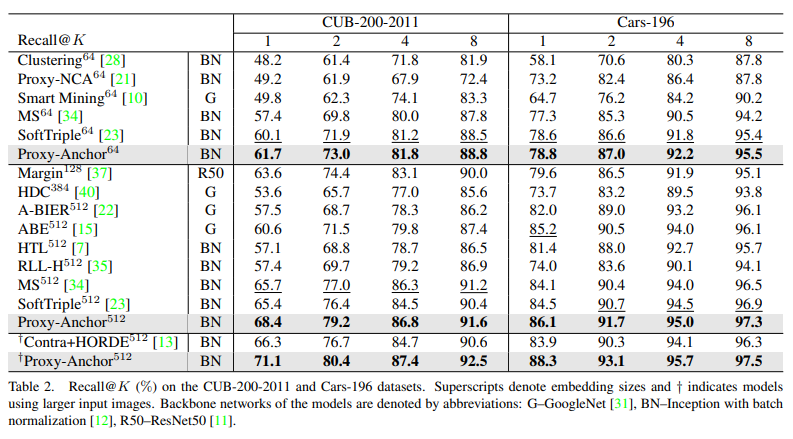
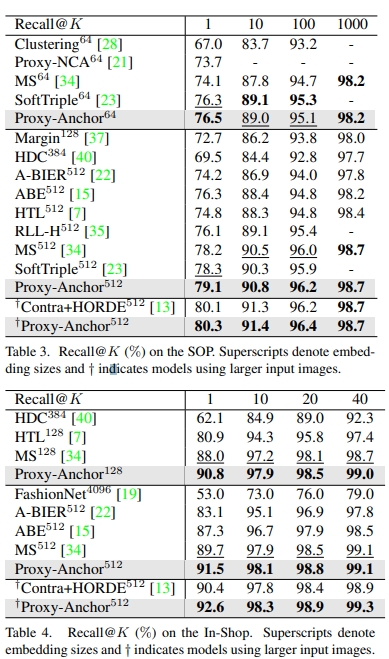

4개의 데이터셋에서 정량적인 결과에서 SOTA를 달성한 결과를 볼 수 있다. 또한 정성적인 결과, Fig 4에서 보이는 바와 같이 유사해 보이는 hard negative case에서도 다른 방법론보다 좋은 결과를 보여준다.
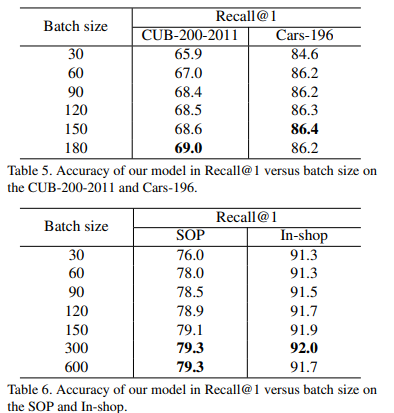
또한 batch 크기 별 실험을 통해 해당 방법론이 batch 내 정보를 이용하여 데이터 연관성을 이용한다는 것을 증명한다.
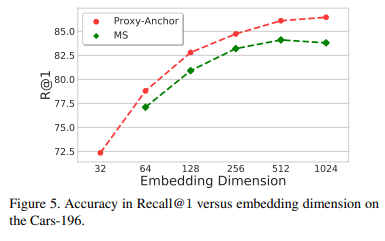
또한 embedding dimension 크기에 따른 성능 변화 실험을 보여준다. MS loss에 비해 보다 큰 dimension에서도 점점 좋은 성능을 보여주고 있다.

또한 loss의 하이퍼 파라미터 margin δ>0, scaling factor α>0 에 따른 성능 변화를 보여준다. α인 경우, 16 이상에서부터 좋은 성능 보여주고 있으며, δ인 경우, 값이 커지면서 성능이 향상되는 모습을 보여주지만, α가 커지면서 성능이 오히려 감소하는 경향성을 보여주고 있다.
========================================================
해당 loss는 지금 연구 중인 자기지도 학습 기반 병해 위치 검출 연구를 위해 찾아보게 되었습니다. 쭉 읽으면서 지금 그리고 있는 방향성에 매우 적합한 loss라고 생각이 들었습니다. 현재 코드 레벨에서 살펴보고 있으며, 해당 방법론을 통해 좋은 결과를 얻었으면 좋겠습니다.