[CVPR 2018] PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space

지난 PointNet 의 단점들을 보완한 point cloud 를 input으로 하는 더 발전된 형태의 network 인 PointNet++ 입니다. 실제로 point cloud 를 이용한 3D Detection 모델은 대부분 이 모델을 더 많이 이용하는 것으로 보입니다.

Introduction

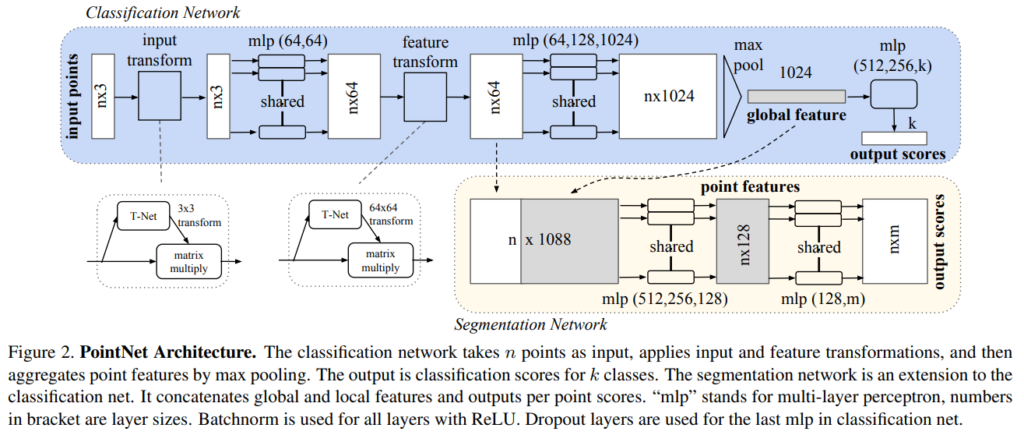
지난 PointNet 모델은 point cloud 를 가공하지 않고 raw 한 형태로 이용한 혁신적인 형태의 모델이었습니다. 하지만 이 모델에는 큰 단점을 가지고 있었는데 이는 local structures 를 파악하지 못 한다는 단점이 있었습니다. 이렇게 local feature 를 잡아내지 못 하는 PointNet의 단점으로 인해 fine-grained patterns 나 복잡한 구조를 파악하는 능력이 부족했다고 합니다. 지난 구조를 살펴 보면 PointNet 의 Segmentation 모델에서 특정 지점의 point feature 를 local feature 를 담고 있다고 보고 global feature 와 concat 해서 사용하는 것을 볼 수 있습니다. 하지만 이것으로는 local feature 를 잡아내기에 충분하지 않았나 봅니다. 이러한 이유로 생각해보았을 때 PointNet 은 이미지 내 모든 Point 를 한번에 처리하게 되서 이러한 문제가 발생하는 것인가 라고 생각했습니다. 일반적인 이미지처리를 위한 Conv Net 을 생각해보아도 일정한 크기의 kernel 이 계층적으로 쌓여서 특정 receptive field 를 파악하는 형태로 이루어 집니다. 이번 논문에서 제안하는 개선된 형태의 PointNet 도 이렇게 local feature 를 잡아내기 위해서 모든 Point 를 한번에 처리하지 않고 특정 group 별로 처리하게 되며, Conv Net 과 같이 hierarchical 한 구조로 만들어지게 됩니다.

Method

Review of PointNet

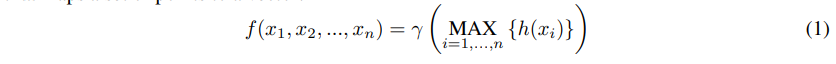
해당 논문에서는 PointNet 을 위와 같은 식으로 표현했습니다. 위 함수는 unordered point set {x_1, x₂, …, x_n} (x_i ∈ R^d , d: coordinates dimension) 이 주어졌을 때 f: X -> R 의 points to vector 매핑 함수입니다. 이때 r, h 는 주로 multi-layer perceptron networks 로 구성됩니다. 위 함수는 input point permutation (unordered point set) 에 대해서 invariant 하고 이 points 를 통해서 공간적 특징을 encoding 할 수 있습니다. 그러나 different scales 에서 local context 를 파악하는데는 다소 어려움이 있다는 단점이 있습니다. 그렇기에 해당 논문에서는 a hierarchical feature lerning framework 를 도입하게 됩니다.

Hierarchical Point Set Feature Learning

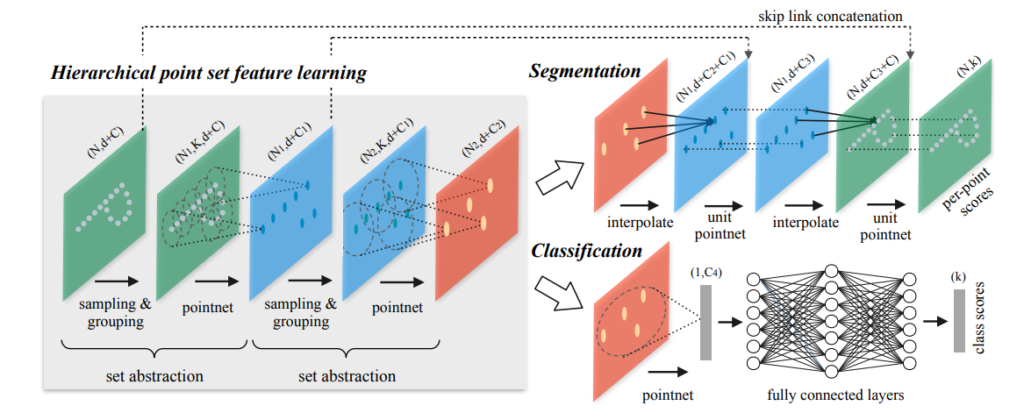
PointNet 에서는 single max pooling 을 통해서 전체 point set 에서 정보를 종합하게 됩니다. 해당 논문에서 제안하는 새로운 architecture 에서는 a hierarchical grouping of points 를 해당 hierarchy 를 따라 점점 더 큰 local region 의 feature 를 추출하나갑니다.

해당 hierarchical structure 는 몇 개의 set abstraction levels 라는 구조로 이루어지게 됩니다. 각각의 level 에서 a set of points 가 feature 를 추출한 더 적은 원소로 구성된 새로운 set 을 만듭니다. The set abstraction level 은 three key layers 로 구성됩니다: Sampling layer, Grouping layer, PointNet layer. Sampling layer 에서는 input points 로 부터 a set of points 를 선택하게 되는데 그러면서 local regions 의 centroids 도 정의하게 됩니다. Grouping layer 는 해당 centroids 의 주변 points 를 통해서 local region sets 를 구성하게 됩니다. 마지막으로 PointNet layer 는 원래 PointNet 의 기능인 local region patterns 를 feature vectors 로 encoding 하기 위해서 mini-PointNet 구조를 사용합니다.

A set abstraction level 은 N * (d + C) matrix 형태의 input을 받게됩니다. 여기서 N 은 d-dim coordinates 와 C-dim point feature 를 갖는 points 개수 입니다. ouput 으로는 N’ * (d + C’) 형태의 matrix 이고 local context 를 포함하는 d-dim coordinates, 새로운 C’-dim feature vector 의 N’ 개의 subsampled 된 points 입니다.

Sampling layer

input points {x_1, x₂, …, x_n} 가 주어졌을 때 여기에서는 farthest point samping (FPS) 라는 방법을 통해서 a subset of points {x_i1, x_i2, …, x_im} 을 선택하게 된다. 이 방법은 {x_i1, x_i2, …, x_ij-1} 과 가장 거리가 먼 점 x_ij 을 선택하는 방식으로 진행됩니다. 해당 방법은 같은 개수의 centroids 를 선택할 때, random sampling 에 비해서 전체 영역을 더 잘 커버할 수 있도록 선택하게 된다고 합니다. CNN 이 data distribution 에 무관하게 항상 특정한 영역을 scan 하는 것과는 다르게, 해당 sampling 방법은 data dependent manner 로 receptive fields 를 만들게 된다고 합니다. 이 말을 생각해봤을 때 CNN 은 항상 특정 크기의 kernel 로 진행되기 때문에 항상 일정한 크기의 receptive fields 를 갖지만, point cloud 는 거리 등 여러 요소에 따라 특정 지역의 data distribution 이 달라지게 되고 그에 따라 receptive fields 가 변경될 수 있어서 그런 것 같다고 생각했습니다.

Grouping layer

이 layer 의 input 으로는 N * (d + C) size 의 point set 과 N’ * d size의 a set of centroids를 받게되고, ouput 으로는 N’ * K * (d + C) size 의 groups of point sets 이 됩니다. 여기서 각 group 은 a local region 에 해당되고, K 는 centroid points 의 주변 points 개수가 되며 이 K는 group 마다 상이할 수 있습니다.

CNN 에서는 a local region of pixel 이 array indices 와 함께 Manhattan distance (kernel size) 에 의해 구성됩니다. metric space 에서 sample 된 point set 에서는 neighborhood of a point 는 metric distance 에 의해 정의됩니다.

group 을 만들기 위해서 여기서는 ball query 혹은 knn 을 이용하게 됩니다. ball query 는 특정 반지름 내에 있는 모든 points (K 개 이하) 를 찾습니다. knn 은 K nearest neighbor 를 찾게됩니다. KNN 과 비교했을 때 ball query 는 고정된 region scale 를 보장하기 때문에 더 선호된다고 합니다.

PointNet layer

이 layer 의 input 으로는 N’ * K * (d + C) 의 size 를 가지는 N’ 개의 local regions of points 를 받게됩니다. output 으로는 N’ * (d + C’) size 형태로 나오게 되며 각 centroids 마다 local region 이 추출되고 해당 local feature 가 the centroid’s neighborhood 를 encoding 하게 됩니다.

local region 에서 points 의 coordinates 는 a local frame relative to centroid point 로 변환되게 됩니다: x_i^(j) = x_i^(j) – x̂^(j) for i = 1, 2, …, K and j = 1, 2, …, d, x̂ 는 centroids 좌표. 이렇게 상대 좌표를 사용함으로써 local region 안에서 point-to-point relations 를 찾아낼 수 있게 됩니다.

Robust Feature Learning under Non-Uniform Sampling Density

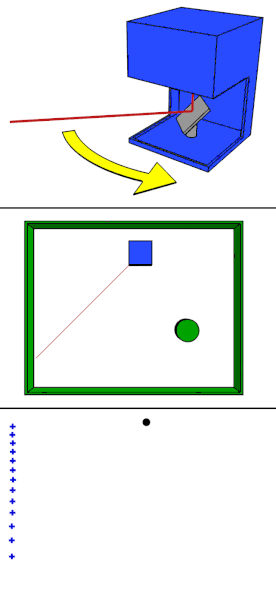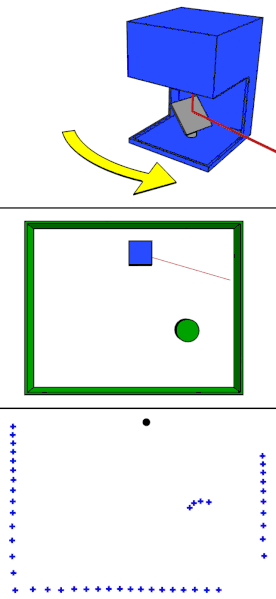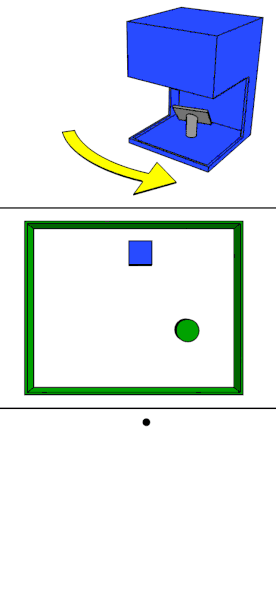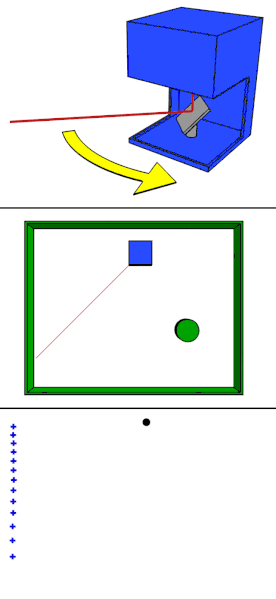
point set 은 area 별로 non-unoform density 를 갖는 것이 일반적이다. 이러한 non-uniformity 는 point set feature learning 에 상당한 어려움을 줍니다. dense data 에서 학습된 features 는 sparsely sampled regions 에서 제대로 작동하지 않을 것이고, 따라서 sparse point cloud 에서 학습된 모델도 fine-grained local structures 를 찾아내지 못 할 것입니다.

우리는 finest details 를 잡아내기 위해 densely sampled regions 에서 가능한 closely 하게 points 를 확인하고 싶지만 low density areas 에서는 이러한 것이 불가능 합니다. 이럴 때는 더 큰 scale의 patterns 를 찾아내야 합니다. 이러한 목표를 달성하기 위해 여기서는 input sampling density 가 변할 때 different scales 의 regions 으로부터 features 를 합성하도록 학습하는 density adaptive PointNet layers 를 제안합니다.

위에서 설명한 Hierarchical 한 구조에서는 각 abstraction level 은 single scale 에 대해서 작동하게 됩니다. PointNet++ 에서는 각 abstraction level 은 multiple scales of local patterns 를 추출하여 합성하게 됩니다. grouping local regions 와 combining features from different scales 에 따라 두 가지 형태의 density adaptive layers 를 제안합니다.

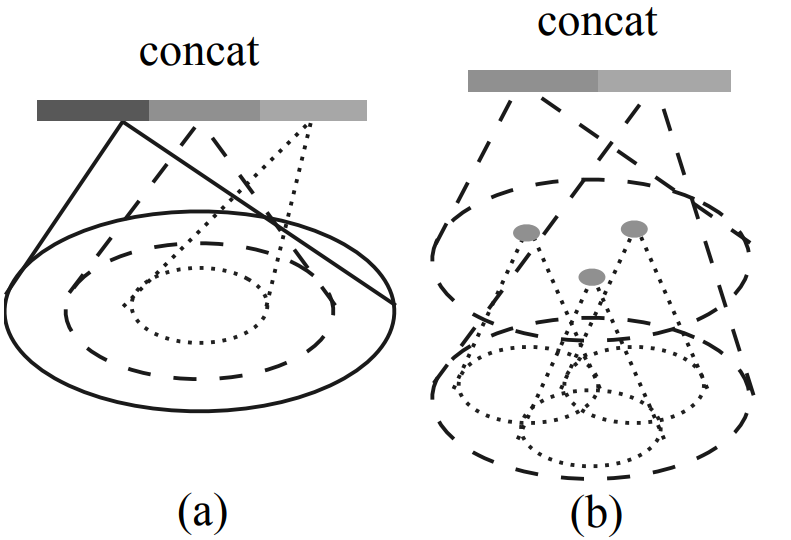
Multi-scale grouping (MSG)

첫번째 방법으로는 Fig 3 (a) 에서 보이는 것과 같은 방법으로 Multi-scale grouping 이 있습니다. 이는 다양한 scales 에서 grouping 단계를 적용하고 추출된 features 를 concatenate 하는 방법입니다. 이는 input points 에 대해 random 한 확률로 droping out 을 하며 진행되는데 이를 random input dropout 이라고 합니다. 각 training point set 에 대해서 dropout ratio θ 가 uniform 한 랜덤 확률 [0, p] (p < 1.0) 에서 선택되고, empty point set 을 피하기 위해서 p = 0.95 로 선택되었다고 합니다. 이렇게 함으로써 network 에 various sparsity 와 varying uniformity 를 가진 training set 을 제공할 수 있게 된다고 합니다. test 때에는 가능한 모든 point 를 사용합니다.

Multi-resolution grouping (MRG)

위의 MSG 방법은 scale 별로 계속 모든 point에 대해서 계산이 이루어져야 하기 때문에 computation 이 너무 expensive 하다고 합니다. 이를 피하기 위한 Fig 3 (b) 에서 보이는 것과 같은 multi-resolution grouping 이 있습니다. 이는 expensive computation 라는 위 MSG 방법의 단점을 보완한 방식입니다.

위 Fig 3 (b) 그림으로 해당 구조를 살펴보자면 특정 level L_i 에서 얻어진 features of region 이 concatenation of two vectors 로 표현된 것을 볼 수 있습니다. 왼쪽의 한 vector 는 low level L_i-1 에서 set abstraction level 을 이용해서 얻어진 feature 이고 오른쪽 다른 vector 는 local region에서 모든 raw points 를 직접적으로 이용해서 얻어진 feature 입니다.

density of local region 이 low 하면 두 번째 vector 가 더 reliable 하게 되고, high 하면 첫 번째 vector 가 더 reliable 하게 된다고 합니다. 이는 low 할 경우 data 가 너무 sparse 해서 close 하게 확인하기 어렵기 때문에 더 큰 resolution 에서 추출한 vector 가 더 reliable 하게 되고, high 할 경우 close 하게 확인하기 충분히 dense 하기 때문에 더 local feature 를 잘 추출할 수 있게 되기 때문이라고 생각합니다.

Point Feature Propagation for Set Segmentation

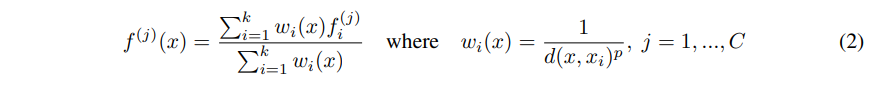
set abstraction layer 를 거치면서 original point set 이 점차 subsampling 되면서 크기가 줄어들게 됩니다. 하지만 set segmentation task 에서는 모든 original points 에 대한 point features를 얻기를 원합니다. 한 가지 해결책으로는 set abstraction level 에서 항상 모든 points를 centroids 로 sampling 해서 진행하는 방법이 있지만 이는 computation 에 있어서 너무 high cost 입니다.

여기서는 이러한 문제를 interpolation 기반의 hierarchical propagation strategy를 이용해서 해결하게 됩니다. feature propagation level 에서 point features 는 N_l * (d + C) points to N_l-1 로 propagate 됩니다. 여기서 N_l , N_l-1 은 set abstraction level l 에서의 input, output size 입니다. interpolation 방법으로는 knn 기반의 방법이 사용된다고 하며 original point set 을 얻을 때까지 해당 방법을 반복해서 적용한다고 합니다. 이 방법은 위 Eq (2) 와 같은 식으로 나타낼 수 있습니다 (default p=2, k=3).

이 방법에 대해서는 추상적으로는 이해가 되나 완전하게 이해가 되지는 않은 것 같습니다…

Experiments

Point Set Classification in Euclidean Metric Space

MNIST

우리가 잘 알고있는 MNIST 데이터셋입니다. 2D 이미지를 2D point cloud 형태로 변환하여 input으로 사용했는데, 기존 PointNet과 비교했을 때 더 좋은 성능을 보이고 있습니다.

ModelNet40

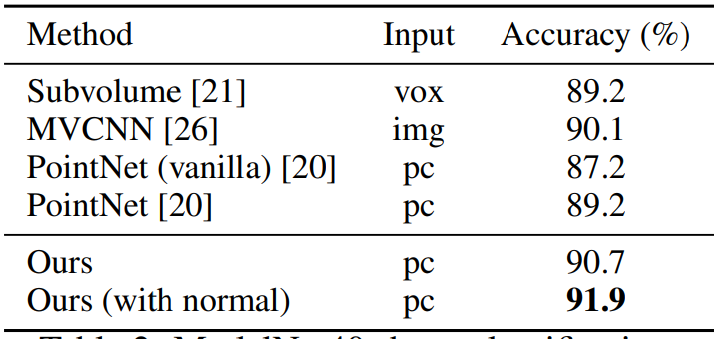
ModelNet40 데이터셋은 40개의 CAD 모델에 대한 데이터셋입니다. 해당 데이터셋에 대해서도 기존 PointNet 보다 더 좋은 성능을 보이는 것을 알 수 있습니다.