안녕하세요. 첫… 리뷰입니다. 저는 첫 X-Review에서 논문은 아니고, 제가 지난주에 공부한 SIFT와 BoVW, 그리고 Vlad에 대해 정리한 내용을 쓰기로 했습니다. 내용이 길어 최대한 압축했습니다. 여러 자료를 참고하여 정리하였으므로, 출처를 중간중간 남기면서 글을 작성했습니다. 그럼 시작하겠습니다.
SIFT
SIFT : Scale-Invariant Feature Transform / 이미지의 크기와 회전에 불변하는 특징을 추출하는 알고리즘
참고로 SIFT (Scale Invariant Feature Transform)의 원리를 기반으로 작성하였습니다. 아래 블로그는 6가지 단계로 좀 더 세분화 하여 설명하였는데, 저는 논문을 기준으로 단계를 다시 나누어 정리하였습니다.
먼저 “Scale space”라는 것을 만들어야하는데, 이름에서 유추할 수 있듯이 다양한 스케일(크기)의 이미지들을 모아둔 것이라고 한다. 이 부분에서 스케일을 조정할때는, 실제 크기를 바꾸는 것이 아니라 blur(일반적으로 가우시안 필터 사용)를 이용해서 크기를 고정하는 식으로 조정한다고 한다.
이렇게 만들때, Octave라는 개념도 등장한다. Octave를 사전에서 검색해보면, “어떤 음에서 완전 8도의 거리에 있는 음정. 또는, 그 거리. 물리학적으로는 진동수가 2배 되는 음정. 팔도 음정.”라는 뜻을 가지고 있는데, blur되는 이미지들의 묶음을 Octave라고 생각하였다. 하나의 Octave에서는 이미지가 K배씩 blur되도록 조정하는 식으로 Scale space를 만든다.
그럼 여기서 왜 이미지들을 이런식으로 blur해서 묶을까? 그 이유는 극값을 알아내기 위해서이다. Laplacian of Gaussian(LoG)를 사용하면, 이미지내의 엣지와 코너를 알아낼 수 있다. 하지만 우리는 Difference of Gaussian(DoG)라는 연산을 통해 계산한다. DoG는 LoG에 비해 연산량이 작고, 정규화 과정이 포함되어 있어 더 장점이 있다고 한다. 실제 DoG연산은 우리가 만들어낸 Scale space의 Octave의 이미지들에서 인접한 두 이미지를 빼는 식으로 쉽게 구할 수 있다. 이렇게 계산한 이미지는 DoG 이미지라고 부른다.
우리는 DoG 이미지를 통해 극값을 구할 수 있다. 지금 체크하는 픽셀의 값이 26개의 이웃 픽셀값 중에 가장 작거나 가장 클 때 극값으로 인정하는 식으로, 자신을 포함한 인접한 DoG 이미지(총 3장)을 보고 계산한다.
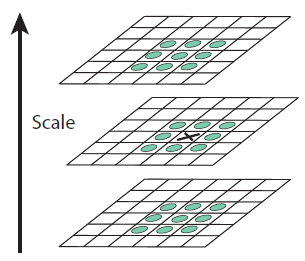
하지만 이렇게 만들어도 극소값, 극대값들의 위치에 접근할 수 없다. 진짜 극소값, 극대값은 픽셀과 픽셀 사이 공간에 위치할 확률이 크기 때문이다. 실제 위치를 구하려면 테일러 2차 전개를 사용한다고 한다. 수학을 잘 못해서 검색을 조금 했더니, 테일러 급수의 유도와 의미를 찾을 수 있었다.
1계 도함수는 바로 옆 포인트와의 관계, 2계 도함수는 양 옆 포인트와의 관계(혹은 바로 옆 포인트와 두번째 옆 포인트와의 관계로 생각할 수도 있다.)등을 설명하고 있는 것이기 때문이다. 따라서, 차수가 높으면 높을 수록 멀리있는 근사화하고자 하는 함수값에서 멀리 떨어진 곳까지도 함수의 근사가 정확해진다. 한마디로 요약하면, 테일러 급수는 특정 point의 도함수 정보를 이용해서 point 주변의 함수 값을 알아내는 방법이라고 할 수 있을 것 같다.
그래서 이 부분을 토대로 생각해보면, DoG 이미지로 계산한 극값을 미분해서 실제 위치에 근사시키는 것으로 이해했다. 여기까지 수행하면 우리는 이제 keypoint라고 부를 수 있는 극값을 많이 추렸다.
keypoint는 코너에 위치해야 활용 가치가 높다고 한다. 그래서 코너에 위치하지 않은 keypoint와 대비가 낮은 keypoint를 제거해줄 필요가 있다. 그럼 코너인지 아닌지는 어떻게 판별할까? SIFT에서는 Hessian Matrix를 사용했다. Hessian Matrix는 함수의 곡률 특성을 나타내는 행렬이라고 한다. 역시 처음보는 내용이라 검색을 했다.
- eigenvalue(고유값) : 화살표가 나타내고 있는 방향은 고유벡터, 그 길이는 고유값을 의미
- eigenvalue가 모두 양수인 경우: 해당 지점에서 함수는 극소값을 갖는다 (아래로 볼록)
- eigenvalue가 모두 음수인 경우: 해당 지점에서 함수는 극댓값을 갖는다 (위로 볼록)
- eigenvalue가 음과 양이 섞여있는 경우: 해당 지점에서 함수는 변곡점을 갖는다 (아래 볼록과 위로 볼록이 교차)
- SIFT에서는 2×2짜리 Hessian Matrix를 계산함
- 이 때, 2×2 행렬 M의 두 eigenvalue를 λ1, λ2 (λ1≥λ2)라 하면 영상 변화량 E는 윈도우를 λ1의 고유벡터(eigenvector) 방향으로 shift 시킬 때 최대가 되고, λ2의 고유벡터 방향으로 shift시킬 때 최소가 됩니다 (why? 그렇다고 합니다 ㅠ.ㅠ). 또한 두 고유값(eigenvalue) λ1, λ2는 해당 고유벡터 방향으로의 실제 영상 변화량(E) 값이 됩니다 (단, 윈도우의 shift 크기가 1일 경우). 따라서, M의 두 고유값 λ1, λ2를 구했을 때, 두 값이 모두 큰 값이면 코너점(corner point), 모두 작은값이면 ‘flat’한 지역, 하나는 크고 다른 하나는 작은 값이면 ‘edge’ 영역으로 판단할 수 있습니다. 실제 Harris 방법에서는 M의 고유값을 직접 구하지 않고 det(M)=λ1λ2, tr(M)=λ1+λ2 임을 이용하여 다음 수식의 부호로 코너점 여부를 결정합니다. 즉, R>0면 코너점, R<0면 edge, |R|이 매우 작은 값이면 R 부호에 관계없이 flat으로 판단 (단, k는 경험적 상수로서 0.04 ~ 0.06 사이의 값).
정리할만한 내용을 뽑으면 위와 같은 내용이었다. Hessian Matrix에서는 eigenvalue라는 것을 이용해서 keypoint가 코너에 위치하는지, 엣지에 위치하는지를 구분해 낼 수 있다고 한다.
우리는 이제 활용 가치가 높은 keypoint를 가지고 있다. 이 keypoint들에게 우리는 rotation invariance를 줄 것이다. keypoint 주변에 윈도우를 만들고, 36개의 bin을 가진 히스토그램을 만든다. 그럼 이 keypoint가 가르치는 방향을 알 수 있다. 가장 높은 bin이 히스토그램의 처음에 오도록 회전시켜 이 keypoint가 rotation invariance를 만족하도록 한다.
사실 앞서 수행한 과정들을 통해 scale invariance를 만족시키고 있다. 그럼 왜 이 불변성을 주는 것인가? 이미지 내에서 keypoint를 추출한다는 것은, 이미지의 크기가 변해도 회전해도 같은 점을 찾기 위해 하는 것이기 때문에 이러한 불변성을 부여한다. 하지만 불변성만 주면 어떻게 같은 keypoint라는 것을 찾을까? 그래서 keypoint에 식별 가능한 정보를 부여한다.
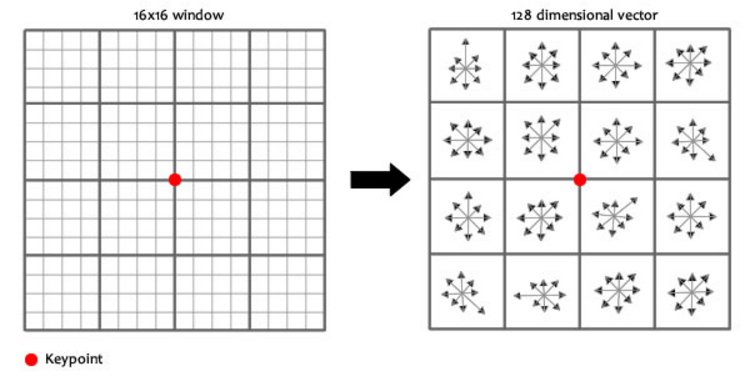
식별 가능한 정보는 위의 그림과 같이 할당한다. rotation invariance와 다르게 여기서는 8개의 bin을 가진 히스토그램을 사용한다. 우리는 위와 같은 과정에서 16×8짜리 숫자 벡터를 얻는다. 이 벡터에서 rotation invariance를 해결하기 위해 keypoint의 방향을 각각의 그레디언트 방향에서 빼고, 밝기 의존성을 해결하기 위해 정규화를 수행하면 SIFT에서 keypoint를 구하는 과정이 끝난다. keypoint간의 값이 최소가 되는 부분을 이제 동일한 keypoint로 계산할 수 있게됬다.
BoVW와 VLAD
BoVW와 VLAD는 SIFT와 같은 방법들을 이용해서 뽑아낸 특징을 이용해서 이미지에서의 visual words(local descriptor)를 뽑아내는 것이라고 이해했다. SIFT를 사용하는 것은 똑같은데, local descriptor를 만드는 과정에서 차이가 있었다.
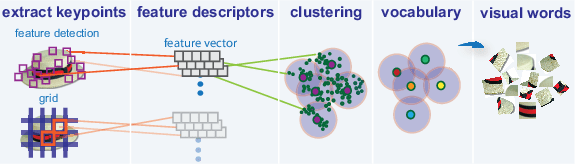
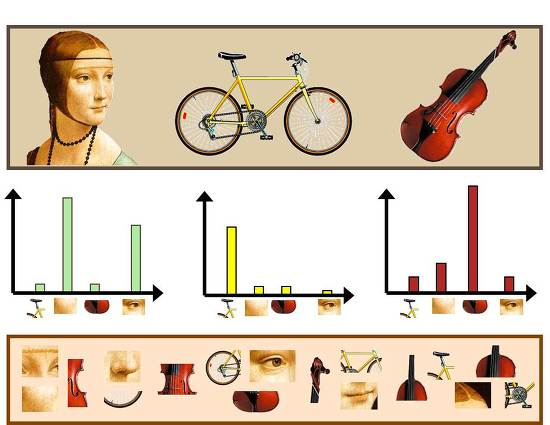
먼저 BoVW는 Bag of Words(BoW)라고 텍스트에서 사용하던 기법을 Bag of Visual Words(BoVW)로 바꾸어 이미지에서 사용하기 시작했다고 한다. SIFT를 통해 뽑아낸 keypoint(code)들을 clustering한다. 이렇게 만들어지는 군집의 중심점을 codeword라고 부른다. 이러한 codeword들이 모이면 codebook이 된다. 우리는 이미지의 특징들이 모인 local descriptor를 만들었다. 그럼 이제 이미지에서 뽑아낸 특성이 codeword와 얼마나 유사한지 비교하고, 이를 매칭해주는 과정을 통해 히스토그램을 만드는데, 이를 통해 이미지를 구분할 수 있게 된다.
정리에는 Bag of Words 기법, Bag of Words (BoW) 이해하기을 참고했다.
다음으로 Vector of Locally Aggregated Descriptors(VLAD)이다. VLAD 역시 SIFT로 만들어낸 keypoint를 사용하는 것 까지는 동일하다. 사실 여기서부터는 참고할만큼 자료가 많았다. 비디오를 이용한 행동 분류, [Github] VLAD/VLAD.py jorjasso/VLAD 그리고 Machine Intelligence – Lecture 5 (Computer Vision, Features, Fisher Vector, VLAD를 참고했다.
VLAD도 BoVW와 같이 clustering을 해야한다. 하지만 여기서 차이가 생기는데 BoVW에서 중심점을 뽑아 codebook을 만들었다면, VLAD에서는 중심점과의 거리를 이용한다. 하나의 cluster내에서 중심점을 뽑고, 그 중심점과 나머지 점과의 거리를 concat하면 VLAD vector가 만들어진다. VLAD는 차원수를 줄이기 위해 보통 PCA와 함께 사용한다.
여기까지가 공부하며 정리한 자료들을 한번 더 압축해서 글로 풀어낸 정리글입니다. 사실 SIFT→BoVW→VLAD 순으로 가면 갈수록… 자료가 없어지더라고요. 그만큼 정리된 내용들이 없어, 나중에 원본 논문을 꼭 읽어봐야 겠다고 생각했습니다. 정리글은 여기까지입니다. 감사합니다.
NetVLAD를 읽는 것이 VLAD를 이해하는데 훨씬 도움이 될 것이라 생각합니다.
시간 나면 꼭… 읽어보겠습니다…!
VLAD vector를 생성하는 과정에 대해 자세히 설명해주실 수 있을까요? cluster에 할당 및 벡터 합을 계산하고 concat하는 과정에 대해 설명되어 있지 않은거 같아 질문드립니다.
Cluster를 만드는 것은 BoVW와 동일하게 kmeans와 같은 방법을 이용합니다. 그리고 Vlad에서는 cluster의 중심점과 개별 descriptor의 거리를 계산하고, 이 거리를 concat해서 하나의 vector로 합치면, VLAD vector가 만들어집니다. 완성된 VLAD vector는 cluster의 갯수 * descriptor의 차원의 모양을 가지는 정도로 알겠습니다…
리뷰 잘 읽었습니다.
리뷰 내용 중 “BoVW와 VLAD는 SIFT와 같은 방법들을 이용해서 뽑아낸 특징을 이용해서 이미지에서의 visual words(local descriptor)를 뽑아내는 것”이라고 하셨는데, 엄밀히 따지면 local descriptor와 visual word는 서로 다릅니다.
SIFT와 같은 hand-craft based feature를 local descriptor라고 부르며 Visual word는 class의 영상들에서 추출한 local descriptor들을 잘 군집시켜놓고 각 descriptor가 어느 군집에 속하는지에 따라서 이를 히스토그램으로 표현한 것을 의미합니다.
또한 Vlad는 local descriptor 군집들의 가장 가까운 중심과 해당 descriptor에 대한 잔차를 이용해 새로운 feature 형식으로 만들기 때문에 이 역시도 visual word라고 보기는 힘들지 않을까 싶네요.
아하… VLAD에 대한 자료가 많이 없어서… BoVW에 빗대서 생각하다보니까 서로 대응해서 그렇게 생각한 것 같습니다. 알려주셔서 감사합니다.
광진이가 이해를 잘못했구만?
열심히 정리하긴 했는데, VLAD로 가니까 자료가 많이 없어서 어렵더라고요. 나중에 꼭… 보충하겠습니다 ㅠㅠ