Pixel Level prediction 방법론에서 영상과 영상을 비교할때 제일 많이 사용되고 있는 방법론인 SSIM을 좀 더 자세히 이해하고 문제를 찾기 위해서 이 논문을 읽게 되었습니다. Self Supervised Depth estimation 에서 Warping target image와 target image를 비교할때 사용되며 이 매트릭은 매우 중요한 역할을 하고 있습니다. 영상 비교를 위한 메트릭으로써 사이테이션이 무려 2만이 넘는 방법론이지만 이 방법이 과연 Depth estimation에 도움만 주고 있을까 생각이 들었고, 이 매트릭의 문제점이 무엇인지 알기 위해서 읽고 과연 이 논문에서 말하는 문제점이 Depth estimation에 어떠한 문제가 있을지 고찰해보았습니다.
- Introduction
SSIM은 굉장히 유명한 metric이라서 장점에 대한 논쟁의 여지가 없습니다. 하지만 그 유명세에도 불구하고 이 metric에 대한 조사는 별로이루어져 있지 않았으며, 이 논문에서 분석 결과 논쟁이 될만한 흥미로운 특징들이 있다고 합니다. 이 논문에서는 SSIM을 수학적으로 분석하며 직관적으로 문제가 될 수 있는 부분들을 보여줍니다. 결과적으로 SSIM을 이용해서 Image quility를 계산하여 딥러닝의 Loss function으로 사용할 경우 신경망 훈련이 잘못된 방향으로 될 수 있음을 시사합니다.
이 논문에서는 먼저 SSIM이 수식적으로 어떻게 작동하는지 알려줍니다. A와 B이미지의 SSIM을 계산할 경우 식은 다음과 같습니다.
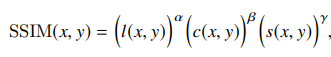
각 영상의 모든 픽셀에 대해서 SSIM을 계산하며 픽셀 주위에 평균, 분산, 공분산을 계산하기 위해서 11×11 사이즈의 가우시안 필터를 이용했습니다. 식에서 l, c,s는 각각 luminance(명도), contrast(대비), structure(구조) 를 의미합니다. 모든 요소들의 식들은 다음과 같습니다.
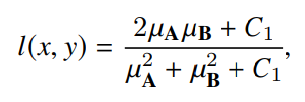
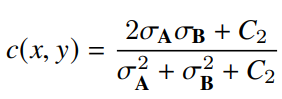
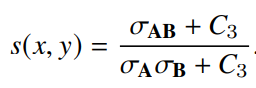
Wang et al에서 제안된 방법으로 C3=(C2)/2 로 정의 되었습니다. 따라서 C3=(C2)/C2와 α = β = γ = 1를 식 1에 대입하면 다음과 같은 식을 얻습니다.
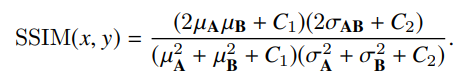
위 식과 같이 SSIM은 각 픽셀 주위 패치에 대해서 명도, 대비, 구조를 계산하여서 두 영상을 보다 세부적인 요소를 평가하게 됩니다.
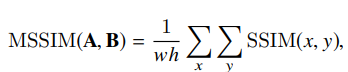
모든 픽셀에 대해서 평균을 취하게 되면 일반적으로 SSIM을 사용할때 쓰는 정석적인 식이 됩니다.
2. Mathematical Properties
이 섹션을 통해서 SSIM 속 각 요소들에 대해서 분석하고 그에 대한 영향을 다음 섹션에서 설명합니다. 먼저 각 요소들이 최소가 되는 순간들에 대해서 아래 그림을 이용해 설명합니다. 논문에서는 그림 외에도 각 식에 대해서 증명을 통해 설명하지만 저는 생략하겠습니다.
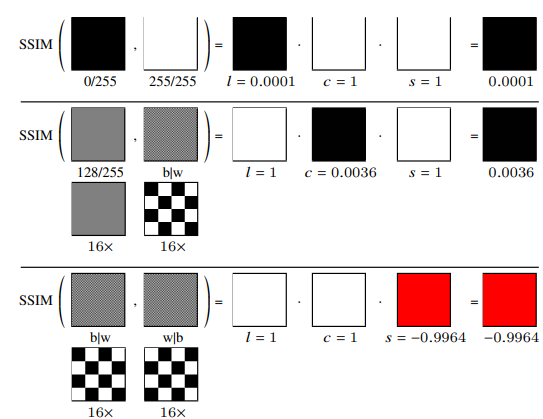
첫번째 줄은 Luminance가 최소가 되는 순간이며 모든 픽셀값이 동일하게 다른 순간입니다. 두번쨰 줄은 Contrast 가 최소가 되는 순간이며, input으로 사용된 것은 모든 픽셀이 중간 값으로 채워진이미지이며 다른 하나는 0과 255 값이 checkboard 패턴으로 채워진 이미지 입니다. 사람눈으로 봤을 때는 동일해보이지만 Contrast에서 차이가 생겨 SSIM이 매우 낮게 평가 됩니다. 마지막 줄은 Structure에 대한 것이며, 입력으로 패턴이 다른 두 checkboard 이미지를 평가할 경우 structure가 음수값을 보이게 됩니다.
위 그림을 보면 모든 요소들의 값은 -1 과 1 사이의 값을 뱉으며 이는 과거 연구들에서 SSIM이 -1과 1 사이의 값을 내뱉도록 설정한 내부 파라미터들에 의해서 그렇습니다. 하지만 이렇게 값의 range만을 위해서 설정되 값으로 이뤄진 SSIM의 경우 원하는 테스크에서 원하는 방향성으로 metric이 동작해줄지 확신할 수 없게 된다고 합니다. 따라서 SSIM 원래 식 1 속 α , β, γ 및 C1,C2,C3를 각 테스크에 맞게 조정하여 원하는 방향성으로 SSIM 조절해야한다고 이 논문에서 주장합니다.
3. Evaluation
이 섹션에서는 각 요소들의 문제점을 시사합니다.
3.1 Luminance
SSIM 속 Luminance는 두 영상의 값 Luminance를 평가하는 것으로 동일한 값차이 날경우 동일한 평가 값이 나와야하는 것이 직관적인 해석입니다. 하지만 이 논문에서 분석하길 명도값이 높을 경우와 낮을 경우에 따라서 평가 값이 다르다고 합니다. 아래 분석 결과들과 함께보면,
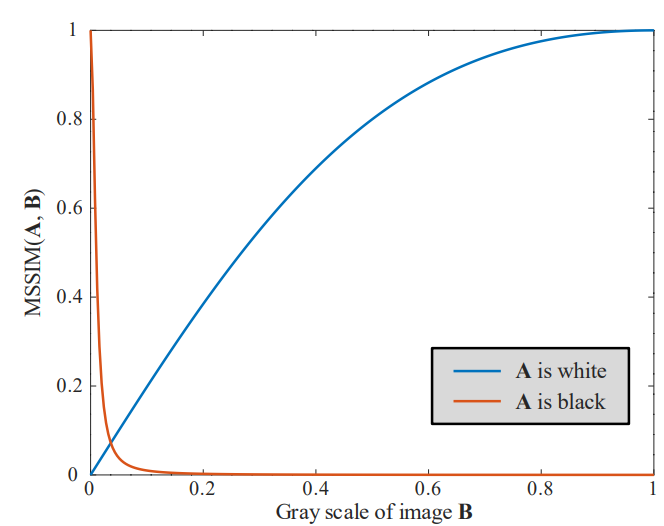
이 분석은 A이미지를 검정과 흰색으로 고정하고 B 이미지의 명도값을 변화시키며 영상의 MSSIM을 계산 한 결과 입니다. 두 결과의 그래프 양상이 확연히 다른 것을 볼수 있습니다. 이 그래프를 간단히 해석하기 위해서 아래 실험까지 보면,
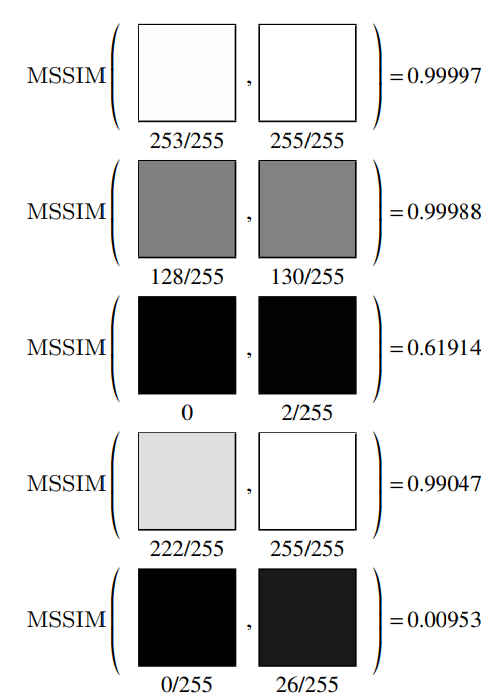
첫번째와 세번재를 보면 , 각각 값이 3 씩 차이 나지만 SSIM이 확연히 다른 값을 보인다. 또한 첫번째와 두번째를 보면 전체적이 값이 더 낮은 곳에서 비교하는 두번째가 더 낮은 SSIM을 보이는 것을 알 수 있다. 이 위 두 분석을 통해서 비슷한 명도 값을 가지는 픽셀들의 비교의 경우 어두울 수록 SSIM이 낮게 나온다는 것이다. ( 이 문제는 사실 Depth estimation에서는 굉장히 critical한 문제가 될 수 있다. 픽셀이 유사하더라도 정확한 값이 아닐 경우 학습에 방해 요소가 되는데, 이 결과에 의하면 명도가 높을 수록 SSIM이 오차를 판단하지 못한다는 것이다. )
3.2 Color
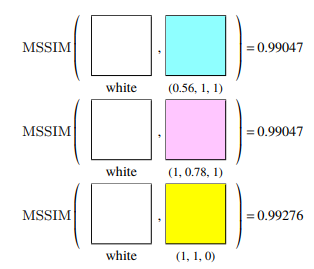
색깔의 문제는 luminance의 문제와 동일합니다. 명도가 높을 경우 눈으로 봐도 다른 색깔을 SSIM으로는 오차로 판단하지 못한다는 것입니다.
5. Conclusions
이 논문에서는 SSIM의 수학적 속성을 분석했으며 인간 시각 시스템의 속성을 준수하지 않음을 보여주었습니다. 이는 기존 SSIM의 목적이 아니였기에 놀라운 점은 아니지만, 현재 매우 다양한 분야에서 당연하게도 이 metric을 사용하고 있기에 너무 맹신하고 사용하는 부분을 바로 잡았습니다.
이 논문의 목적은 SSIM의 대한 맹신은 잘못된 방향으로 연구를 안내할 수 있기 때문에 이러한 믿음을 완화하는 것입니다. SSIM이 어떤 경우에는 유용한 결과를 생성하지만 다른 많은 경우에는 우리가 본 것처럼 반직관적인 결과를 생성할 수 있습니다. 이것은 인간이 합성, 렌더링 또는 자연 이미지 간의 차이를 감지하는 방법을 설명하기 위해 개선된 메트릭을 연구할 수 있는 기회를 제공합니다.
마지막까지 이 SSIM에 대한 분석에 대한 해결책을 제시해줄 것 이라 생각했지만… 딱히 없는 것 같습니다.. 허허 그래도 SSIM의 문제점을 파악할 수 있는 좋은 논문이였던 것 같습니다.