MonoDepth1&2

이번 리뷰는 Monocular Depth Estimation의 큰 흐름을 담당하는 논문들인 MonoDepth 1, 2에 대하여 간략하게 정리하였습니다. 워낙 유명한 논문이다보니 이미 X-review로 작성하신 분들이 종종 있어서… 양심 상 1편 2편을 모두 정리하였습니다.

Abstract

그 당시(2016년) 현존하는 Monodepth 방법론들은 성능은 준수하였으나 한가지 큰 문제점이 존재했습니다. 바로 지도학습 기반의 regression 문제로 풀려다보니깐, GT depth가 없으면 학습을 하지 못하는 것이죠.

하지만 광활한 양의 관련 GT 정보를 구하는 것은 매우 어려운 일이기에, monodepth에서는 이러한 GT 없이도 단일 영상 깊이 추정을 할 수 있도록 하는 새로운 제약조건(Loss)들을 제안하였습니다.

Depth Estimation as Image Reconstruction

단일 기반 깊이 추정 분야는 결국 한장의 영상을 통해 깊이를 추정하는 함수, 즉 \hat{d} = f(\bold{I})를 계산하는 것입니다. 현존하는 방법들은 위에서 설명한 것처럼 지도 학습 기반으로 이 문제를 해결하고 있으나 이는 방대한 양의 장소에서 실제 GT 깊이 정보를 구할 수 없다는 현실적인 문제에 직면하여 실용적이지 못합니다.

이를 해결하기 위해 제안하는 방법론은 Image Reconstruction 문제를 통해 깊이를 추정하고자 하였습니다. 즉 곧바로 깊이를 추정하지 않고, 왼쪽 영상을 통해 오른쪽 영상으로 만들 수 있는 Disparity Map을 구하는 것 입니다.( I^{l}(d^{r}) == \tilde{I}^{r}) 또한, 오른쪽 영상에 disparity를 적용해서 왼쪽 영상도 만들게끔 합니다.

이렇게 Disparity를 통해 왼쪽 영상만으로 우측 영상을 생성할 수 있게 되면, 스테레오 깊이 추정 기법과 같이 두 카메라의 Baseline, Focal Length, Disparity를 통해 Depth 계산이 가능해집니다.

Depth Estimation Network

제안하는 방법론은 왼쪽 영상만을 입력으로 하여 Left-to-Right, Right-to-Left Disparity 모두를 계산하게 됩니다. 일반적인 방법으로 그냥 Left 영상만을 통해 Right image를 만들 수 있는 Left-to-Right Disparity(d^{r}를 구할 수 있는데, 이 d^{r}는 Left Image와 Align이 맞지 않습니다.

그래서 Right Image까지 같이 사용하여 Right-to-Left Disparity(d^{l}를 만드는 경우를 생각해보아야 하는데, 이 방식의 경우 추론된 Disparity가 ‘Texture-copy’현상이 발생하고 이를 통해 추정된 Depth도 부정확합니다.

그래서 저자는 최종적으로 Left-to-Right, Right-to-Left Disparities( d^{r}, d^{l})를 모두 계산하여 두 Disparity의 일관성까지 유지함으로써 보다 정확한 Disparity를 추정하도록 하였습니다.

네트워크 구조는 대충 Encoder Decoder 형식으로 Skip Connection을 사용하였으며, 해상도가 2배씩 차이나는 Disparity Map을 총 4단계까지 추정합니다.(대략 디코더 내 CNN 블럭들을 하나씩 지나갈 때 마다 나오는 Disparity를 사용하는 듯?)

Training Loss

Loss는 Appearance Matching Loss, Disparity Smoothness Loss, Left-Right Disparity Consistency Loss까지 크게 3가지로 구성되어 있습니다.

Appearance Matching Loss는 SSIM과 L1 Loss를 사용하는 것으로, 쉽게 생각하면 실제 영상과 Reconstruction된 영상 사이가 닮게끔 하기 위한 것으로 보면 됩니다.

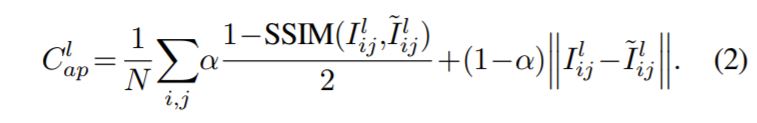
N은 픽셀의 개수를, I, \tilde{l} 는 원본 영상과 Reconstruction 영상을 의미합니다.

Disparity Smoothness Loss도 간단한데, 생성된 Disparity Map이 물체의 외곽 지역에서 부드럽게 연속적이지 못하고 뚝뚝 끊기는 현상이 발생하여 이를 해결해주기 위해 Disparity Map에서의 Gradient를 사용하여 스무딩이 되도록 학습한 것 입니다.

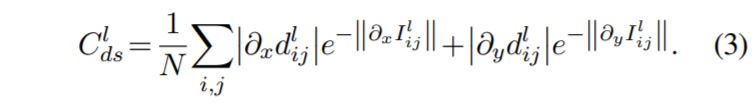
마지막으로 Left-Right Disparity Consistency Loss란 해당 모델이 왼쪽 영상 한장만으로 왼쪽과 오른쪽 영상의 Disparity를 다 계산하게 되는데, 이때 두 Disparity는 항상 일관성 있게끔 해주기 위해 패널티를 부여해주는 것입니다.

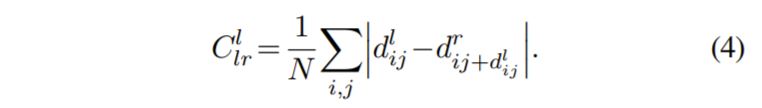
수식도 매우 간단합니다. 그냥 오른쪽 Disparity Map에서 왼쪽 Disparity 값만큼 픽셀을 이동시켜주었을 때 그 위치에서의 왼쪽 Disparity Map과 같게끔 L1 Loss를 적용해야 합니다.

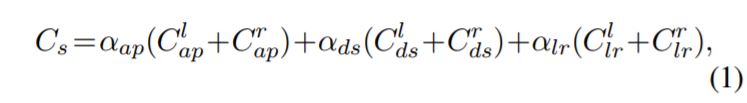
이렇게 각각의 Loss를 계산했다면 이를 다 더해주면 되는데, 위에 3가지 Loss는 왼쪽과 오른쪽 Disparity 각각에 대해 모두 계산하여 더해주게 됩니다. 그리고 위에서 설명했듯이 디코더가 4개의 순차적 스케일을 지니는 Disparity Map을 추론하기 때문에, C_{s}는 1~4개의 합을 다 더해서 최종적인 C가 계산됩니다.

Evaluation

논문에서 보이는 실험 결과들이 상당히 많은데 한번 정리해보겠습니다. 먼저 서로 다른 영상 변환 모델의 결과에 대해 살펴봅시다.

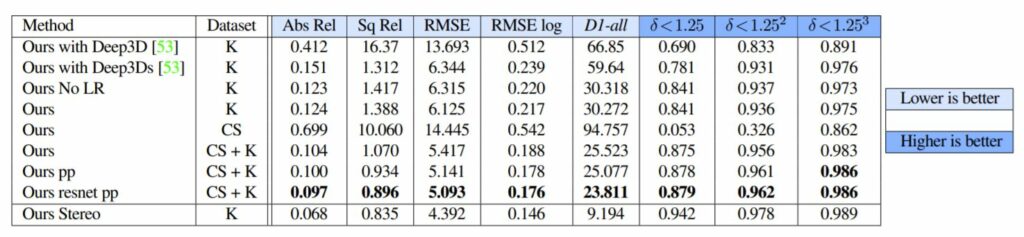
K는 Kitti Dataset, CS는 City Scape Dataset을 의미합니다. 위의 결과를 요약하자면 Left-Right Consistency Loss가 정량적인 결과에서도 미세하지만 더 좋은 효과를 보여주고 있습니다.

또한 Dataset을 Kitty와 City Scape를 섞어서 사용하였을 때 더 좋은 성능 향상일 일으킬 수는 있었으나, City Scape만을 사용하게 될 경우 성능이 많이 감소했다고 합니다. 저자는 아무래도 Kitty와 CS 데이터셋의 카메라 캘리브레이션 값이 달라서 생기는 문제로 보고 있지만, 그럼에도 둘을 같이 사용했을 때 성능이 향상되는 것은 분명하다고 얘기하네요.

위에 그림은 Deep3D와 MonoDepth의 Reconstruction Error, Disparity Map에 대한 정성적 결과입니다. Deep3D의 경우 Reconstruction Error는 잘 만들어 내고 있으나, Smoothness Loss가 없어서 Disparity Map이 상당히 거칠고 부드럽지 못한 것을 확인할 수 있습니다.

하지만 Deep3D에 Smoothness Loss를 적용해주면 이전 대비 깨짐도 적고 상당히 visual이 좋게 나왔습니다. 물론 MonoDepth가 더 좋은 결과를 보이고 있긴 하지만, Smoothness Loss의 역할을 확실하게 보여주는 결과입니다.

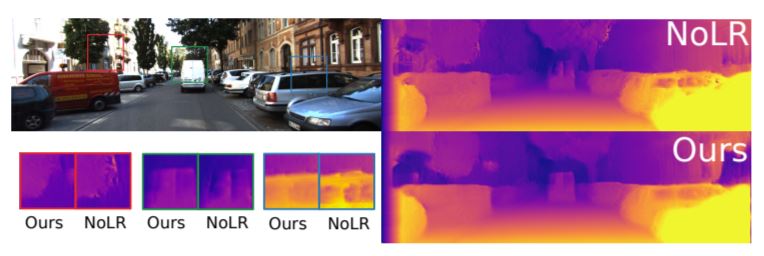
다음은 Left-Right Consistency Loss 입니다. 해당 제약 조건이 없을 경우 전체적으로 Disparity Map이 선명하게 추정이 되지 못한 것을 확인할 수 있으며, Zoom In 된 지점을 보면 보다 확실하게 확인할 수 있습니다.

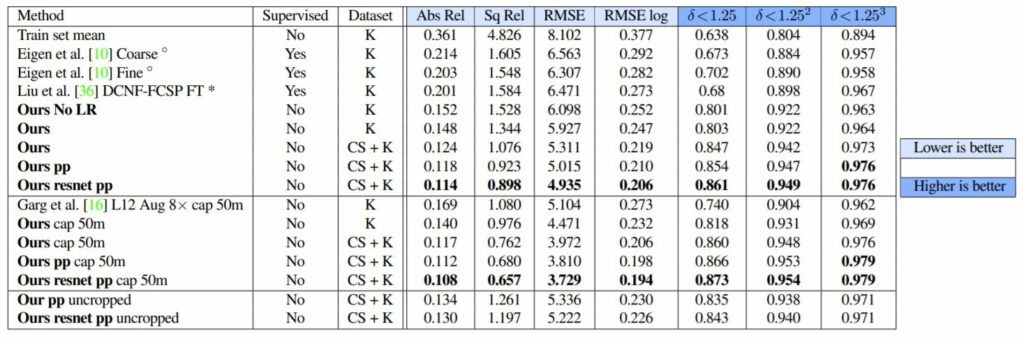
마지막으로 제안하는 방법론과 그 외에 다른 Depth Estimation 기법들과의 비교 실험입니다.

Improved Self-Supervised Depth Estimation

다음은 ICCV2019에 accept된 Monodepth2에 대하여 간략히 리뷰하고 마치겠습니다.

다중 이미지들로부터 Reprojection Error를 계산할 때, 기존의 Self-supervised 방법론들은 이용가능한 Source 영상들의 Reprojection Error를 평균을 취해서 사용하였습니다. 하지만 이 방식은 타겟 영상에서는 보이지만 Source 영상에서는 보이지 않는 지역 등의 경우에서 문제가 발생합니다.

예를들어 모델이 올바르게 Depth를 추정했다 하더라도, 이에 해당되는 지역이 Source 영상에서 Occlusion이 발생했다면 올바르게 Target 영상과 매칭이 되지 않을 것입니다. 그리고 이로 인해서 Photometric Error는 높은 패널티를 부여할 것이구요.

보통 이러한 문제들은 영상 경계면에서의 Egomotion 또는 Occlusion이 발생한 픽셀의 경우 이 문제가 발생합니다. 논문에서는 이러한 두 문제를 해결하기 위해 모든 Source 영상들로부터 Photometric Error를 계산할 시, 평균값을 취하는게 아니라 최소값을 사용하였습니다.

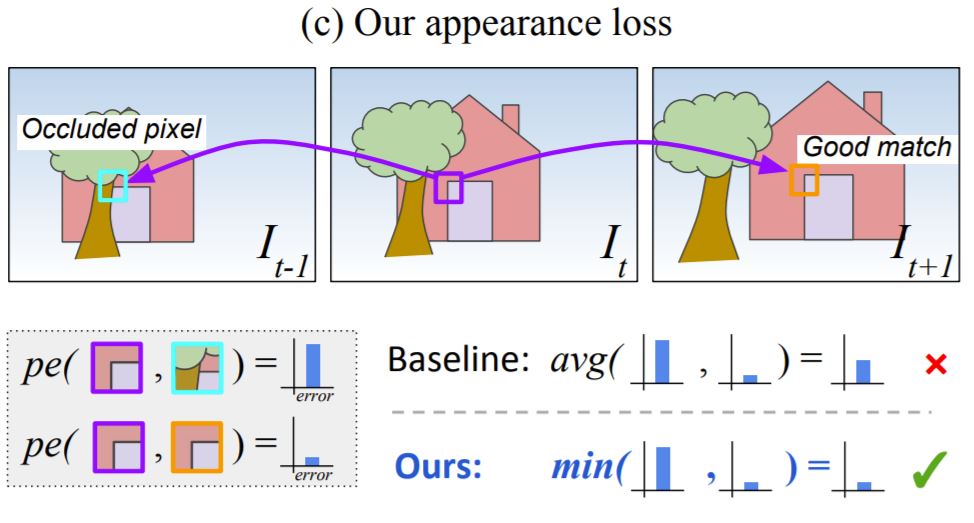
위에 그림을 보시면 이해가 더 쉬울 듯 합니다. \bold{I}_{t}를 기준으로 각각 앞, 뒤 프레임의 영상들이 존재합니다. 이 때 이전 프레임( \bold{I}_{t-1})에서는 문의 좌측 상단 모서리가 나무에 가려 보이지 않지만, 다음 프레임( \bold{I}_{t+1})에서는 분명히 보입니다.

이러한 각 경우에서 이전 프레임과 현재 프레임 사이의 Photometric Error는 당연히 클 수 밖에 없을 것이고, 현재 프레임과 다음 프레임 사이의 Photometric Error는 작을 수 밖에 없을 것입니다. 이 때 기존의 방법론들은 각각의 Error 값을 다 더한 후 평균을 내어 사용하였지만, 제안하는 방법론은 이 둘 중 최소값을 사용함으로써 Occlusion이 발생하였을 때 모델이 받는 Error Penalty를 줄였다고 합니다. 이를 수식으로 표현하면 아래와 같습니다.

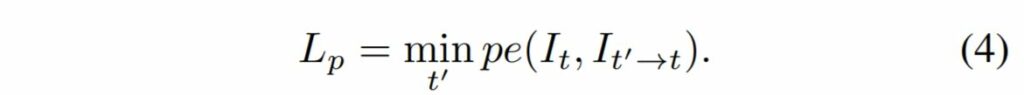
Auto-Masking Stationary Pixels

Self-supervised 기반 단일 영상 깊이 추정 방법론들은 학습 과정에서 두 가지 가정을 세우고 학습합니다. 첫째는 카메라가 항상 움직이고 있는 것이며, 둘 째는 장면은 항상 고정되어야 합니다.

하지만 이러한 가정들이 잘 지켜지지 않는 경우가 종종 있습니다. 예를 들어 자동차가 빨간 불에 멈춰서서 자동차(카메라)가 움직이지 않는 경우이거나, 또는 촬영된 장면 속 물체(자동차)가 움직이고 있는 경우가 있겠죠.

이러한 문제는 Depth Map을 추론할 때 무한대 값을 가지는 Depth 즉 Depth Map에 구멍이 나타나게 됩니다. 이러한 Depth Hole은 학습하는 과정에서 움직임이 물체의 움직임이 관측될 때도 자주 발생합니다.

저자는 이를 해결하기 위해 간단한 Auto-masking 기법을 사용합니다. 해당 기법은 하나의 frame에서 그 다음 frame으로 변화는 과정 동안 어떠한 대상 또는 배경이 외적인 변화가 없이 이전 프레임과 동일하다면 해당 픽셀들을 필터링 해버리는 방법을 말합니다.

이를 통해 네트워크가 동일한 속력으로 달리고 있는 물체를 무시하거나, 또는 자동차가 정차하였을 때 Frame 전체를 무시해버리는 등의 상황에서 효과적으로 대처할 수 있게끔 합니다.

그럼 어떻게 동작하는지 조금 더 자세히 알아봅시다. 저자는 픽셀 당 마스크 \mu 를 사용하는데 해당 마스크는 이진 마스크로 0 또는 1의 값을 가지게 되며 네트워크의 Forward Pass에 따라 자동적으로 계산이 됩니다.

그럼 0 또는 1의 값을 가지는 기준은 무엇일까요? 저자는 만약 차량이 정지해있거나, 또는 거의 동일한 속도로 다른 물체가 움직이고 있다면 앞 뒤 인접한 프레임 사이에 변화가 거의 없는 것을 관측하였습니다.

그래서 저자는 이러한 특징에 따라 만약 인접한 앞, 뒤 프레임을 Target 프레임으로 Reconstruction 할 때의 Photometric Error 값이 Reconstruction을 하지 않은, 순수한 앞, 뒤 프레임의 Photometric Error보다 작은 픽셀만을 사용하도록 \mu 를 설계하였습니다.

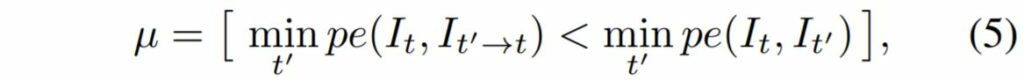
즉 정지해있거나 물체가 동일한 속도로 움직였을 때는 시간이 흘러도 매번 동일한 위치와 외형을 지니고 있기 때문에 동일한 픽셀 값을 가질 확률이 높을 것이며, 이는 Camera Pose를 통한 Reconstruction 과정을 거친 영상( \bold{I_t' \rightarrow t} )보다 더 낮은 Photometric Error를 가질 가능성이 높습니다.

Auto-masking 과정을 거친 경우의 예시 사진입니다. 첫번째 행은 차량이 움직이고 있지만 주변 차량들도 비슷한 속도로 움직이고 있어 인접한 프레임 사이로 비교 시 차량의 위치 변화가 없어 보이는 상황입니다. 두번째 행은 빨간불로 인해 차량이 정지된 상황이구요.

이러한 상황에서 픽셀 단위로 \mu 를 통해 프레임 사이에 변화가 없는 픽셀들에게 0을 부여하였으며, 이러한 검정색 픽셀들은 Loss를 계산하는데 전혀 사용되지 않습니다.

Multi-scale Estimation

기존의 방법론들은 Bilinear Sampler의 Gradient Locality 또는 학습 과정 중 Local Minima에 수렴되는 것을 방지하고자 추론된 Depth Map과 Image Reconstruction을 다중 스케일로 추출하여 Loss를 계산하고, 학습합니다.

하지만 이러한 방법들은 저해상도 영상 속 Low-texture 지역 내에서 Texture-copy Artifact 뿐만 아니라 Depth Hole들을 생성하는 경향성을 가지고 있습니다. (Texture-copy Artifact란 칼라 영상으로부터 Depth Map의 디테일이 부정확하게 변환된 현상을 의미)

이러한 Depth Map 속에 Hole들은 Low-texture 지역 내 저해상도 부분에서 발생할 수 있으며, 이로 인해 Photometric Error가 정확하게 계산되기 힘듭니다.

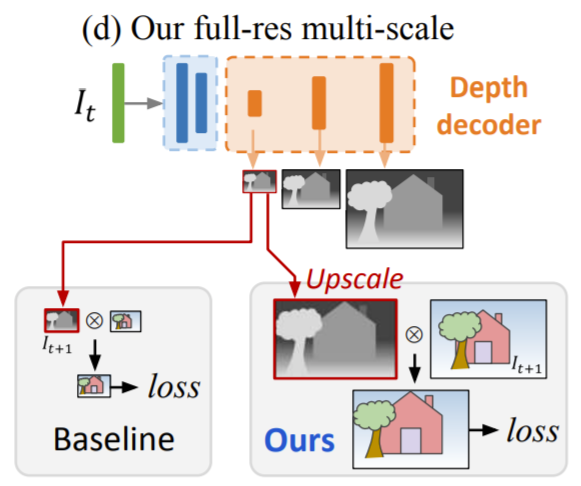
저자는 이러한 문제를 해결하고자 Disparity 영상들의 해상도와 Reprojection Error를 계산하는데 필요한 컬러 영상을 두 개로 나누었습니다. 애매한 표현력을 지닌 저해상도 영상에서 Photometric Error를 계산하는 것 대신에, 저해상도의 Depth Map을 입력 영상의 해상도만큼 Up-sampling 후, Reprojection과 Resampling을 거쳐 고해상도 영상에서의 Photometric Error를 계산하는것입니다.

이러한 과정은 마치 patch 단위로 매칭하는 것과 유사하다고 하는데, 저해상도의 Disparity 값들은 고해상도 영상 속 픽셀의 Patch 전체를 warping 하는 것과 비슷하다고 합니다. 아무래도 저해상도 영상을 억지로 고해상도로 늘렸으니 생성된 영상이 블러해질 수 밖에 없는데 이러한 저해상도 영상 속 픽셀을 고해상도에서 패치로 생각한 것이 아닐까 싶습니다.

아무튼 이러한 방식을 통해 각 스케일 별로 추출된 추론값들이 최대한 고해상도 타겟 영상으로 Reconstruction하도록 학습할 수 있다고 합니다.

Experiments

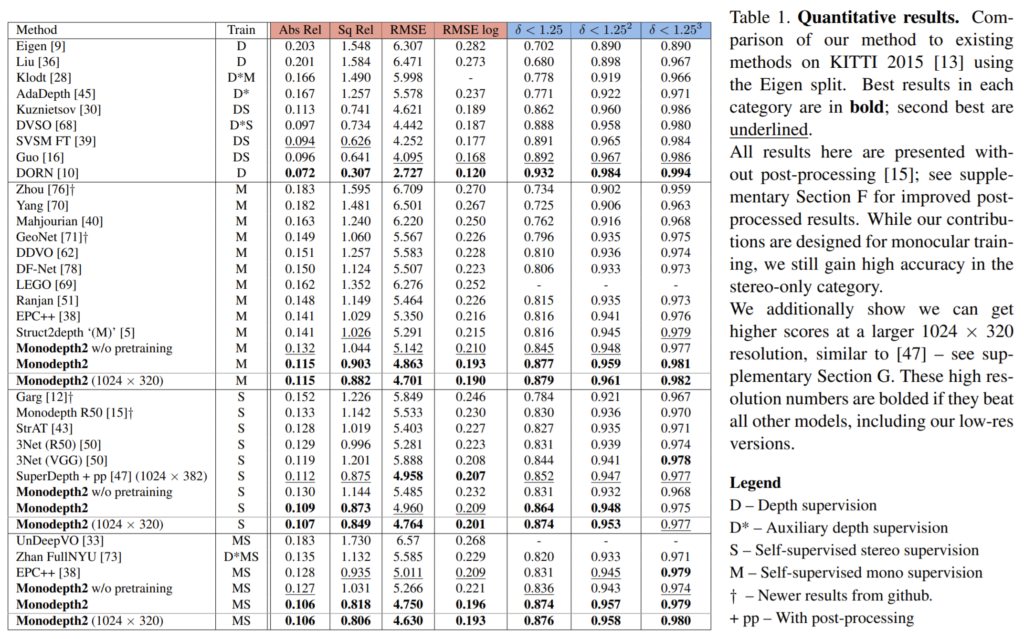
다음은 정량적 결과 표입니다.