이번 리뷰 글은 비지도 학습 기반의 스테레오 매칭 방법론 입니다. 해당 방법론은 스테레오로부터 얻을 수 있는 epipolar constraints를 고려한 attention mechanism을 제안함으로써, disparity variations을 고려하지 않고 추론이 가능하도록 합니다. 또한 이로부터 얻은 matching cost로 cycle consistency를 제안함으로써 비지도 학습이 가능하도록 한 방법론 입니다.
+ 해당 논문은 스테레오 기반의 방법론 뿐만이 아니라 제안한 main module이 추가된 Super Resolution과 High-resolution Stereo Datasets(Flickr1024)을 제안합니다. 이번 리뷰에서는 스테레오 매칭을 주로 다룰 예정 입니다. 관심 있으신 분들은 논문을 찾아보시거나 요청을 해주시면 추가로 작성하도록 하겠습니다.
Intro
CNN 기반의 스테레오 매칭 방법론들은 대부분 3D/4D cost volume을 회귀하여 disparity를 예측합니다. 이러한 방법론의 특징상 disparity의 variation 고정하는 방법을 이용합니다. 즉, Max Disparity 크기의 disparity index 지정해줘야 합니다. 또한 각 index에서의 score로부터 평균 혹은 weighted sum을 통해 aggregation된 값을 이용하여 예측합니다.
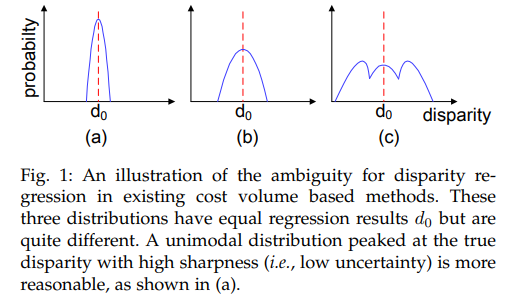
기존의 방법론들은 위에서 언급한대로 Max Disparity를 지정하여 각 disparity index로부터 score를 구하여 최종적인 disaprity를 구하는 방법을 사용합니다. Fig 1-(c)를 통해 기존 방법론에서 disparity를 유추하는 방법을 볼 수 있습니다. 모든 Max Disparity 크기의 disparity index로부터 추론 하기 때문에 모든 값을 고려합니다. fig 1-(a)를 보면 최대 index가 줄어들었기 때문에 보다 score가 높게 평가될 수 있으며, 이는 명백하게 합리적인 결론으로 보입니다. 저자는 이러한 이유로 max disparity를 지정하는 것보단 유연하게 계산하도록 하는 것이 성능 향상에도 도움이 될 것 이라고 주장합니다.
또한 해당 문제는 서로 다른 카메라로 촬영된 데이터 셋에서도 매우 실용적인 기능 입니다. 예를 들어 KITTI인 경우는 max disparity를 192로 설정하며, MiddleBury은 408를 가집니다. 사전에 미리 알아야하는 정보이기 때문에, 이미 계산이 된 세팅이 아니면 자유롭게 사용이 불가능하다는 단점이 있습니다. 해당 방법론은 max disparity가 고려되지 않으며, GT disparity가 없어도 학습이 가능한 비지도 기반의 스테레오 매칭 방법론을 제시하여 실용적으로 활용도가 높은 연구 결과를 제시합니다.
Method
PARALLAX-ATTENTION MECHANISM (PAM)
기존 self-attention mechanism은 Feature map R^{H * W * C} 를 R^{HW * C} 로 reshape하여 R^{HW * C} R^{C*HW } matrix multiplication을 이용하여 feature간(영상에서으 위치가 고려된) correlation을 얻는 방법을 이용합니다.
저자는 스테레오의 특성(epipolar constraints)을 고려하여 응용하는 방법을 제안합니다. 특별한 reshape operation과 geometry aware matrix multiplication을 이용하여 왼쪽 영상 픽셀에서 오른쪽 영상의 epiploar line의 모든 픽셀이 고려된 attention을 계산할 수 있습니다.
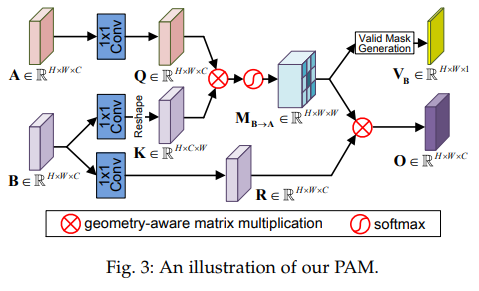
Fig 3을 보면 전반적인 흐름을 이해할 수 있습니다. A, B는 Stereo image pair으로부터 추로된 feature maps에 해당합니다. 두 feature map은 1×1 conv를 이용하여 각각 Query map과 Key map을 생성 합니다. 여기서 Key map은 K \in R^{H*C*W} 로 reshape 후, matrix multiplication과 soft max operation을 걸쳐 parallax-attention map M_{B->A} 를 획득합니다. 이를 통해 A의 한 픽셀에서 수평적인 위치에 해당하는 모든 포지션의 픽셀에 대한 attention score를 구할 수 있게 됩니다. 그 다음 B에 1×1 conv가 태워진 feature map과 M_{B->A} 곱해져 output map O를 추론하며, 그 동안에 M_{B->A} 에 1×1 conv 태워져 occlusion을 고려하기 위한 Valid Mask V가 생성되어집니다.
+ Key map을 reshape하는 이유는 왼쪽 한 픽셀과 평행하게 위치한 오른쪽 모든 픽셀과 계산한다는 말을 생각해보시면 이해하기 쉬울 겁니다.
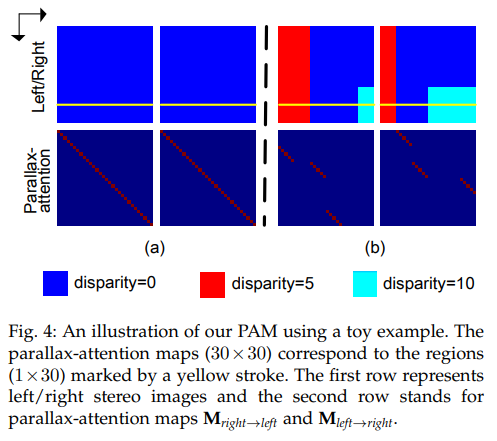
Fig 4를 보면 Parallax-attention map 조금 더 쉽게 이해를 할 수 있습니다. fig 4의 상단을 feature map이라고 가정합니다. 하단은 노란색 선에서의 Parallax-attention map (오른쪽->왼쪽, 왼쪽->오른쪽)에 해당합니다. Fig 4-(a)는 두 disparity가 0에 해당하기 때문에 스테레오 영상에서는 같은 포지션에 집중되며, matrix multiplication이 적용되어져, identity matrix 형태를 가지는 값이 유추됩니다. fig 4-(b) 중 red region(disparity=5)인 경우, (j-5)에 위치한 j 픽셀과 대응되도록 해야 하기때문에 (j, j-5)에 집중해야하는 포인트에 해당합니다. 요약하자면 Parallax-attention map은 두 대응되어야하는 픽셀의 disparity를 간단한 matrix multiplication으로 계산이 가능해지며, 학습을 통해 수동적으로 Max disparity를 입력하지 않고 유연하게 값들을 예측이 가능해집니다.
Left-Right Consistency and Cycle Consistency
저자는 신뢰도 높은 대응점을 획득 하기위해, left-right consistency와 cycle consistency로 구성된 regularize PAM을 제안합니다. 위에서 우리는 Parallax-attention map를 예측하여 sparse한 disparity를 예측할 수 있었습니다. 저자는 이를 이용하여 consistency를 제안합니다.
+ 이해를 돕기 위해 예시를 들자면 potenit에서 R-T를 align 시킬 때, 사용한 방법이라고 생각하시면 쉽습니다.
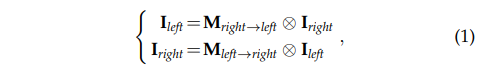
먼저 양방향의 Parallax-attention map를 구했기 때문에, 오른쪽과 왼쪽 영상을 반대로 곱한다면 다른 방향의 영상을 복원할 수 있다고 가정할 수 있습니다.
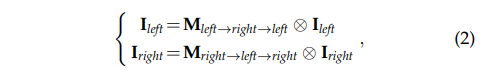
또한 Parallax-attention map을 다시 역으로 한번 더 계산하여 영상에 곱한다면 자기 자신을 복원할 수 있다고 가정이 가능합니다.
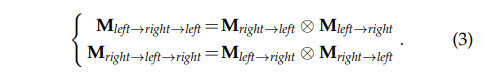
수식 1과 수식 2를 고려한다면 수식 3과 같이 두 파라미터는 서로 상관성을 가지게 됩니다. 즉, cycle-attention maps을 구할 수 있으며, 이를 loss에서 활용이 가능합니다. 이를 이용하여 순환적으로 서로의 값을 보완할 수 있으며 비지도 학습이 가능함을 보여주는 수식에도 해당합니다.
Valid Mask

위에서 우리는 Parallax-attention map을 구하는 방법에 대해 알아왔습니다. 하지만 해당 방법에는 치명적인 단점이 있습니다. 제한 없이 대응 값을 구할 경우, occlusion이 있는 장면에서도 값을 유추하게 됩니다. 해당 장면에서는 아무런 값을 구하지 않는 것이 타당한 경우에 해당합니다. 저자는 이러한 문제를 해결하기 위해, Occlusion에 대한 Valid Mask를 이용하는 것을 제안합니다.
해당 모듈은 굉장히 심플합니다. Parallax-attention map에서 occlusion pixel은 모든 pixel에서 매칭되지 못하기 때문에 모든 값들이 낮은 score를 가집니다. 이러한 특성을 이용하여 일정 임계값 이상의 값만 이용합니다.
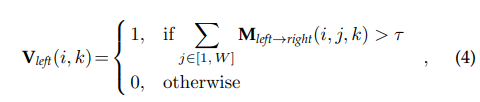
요약하자면 수식 4 값을 Parallax-attention map에 적용하여 occlusion 여부르 확인 가능한 Valid Mask를 제안합니다.
PAM FOR UNSUPERVISED STEREO MATCHING
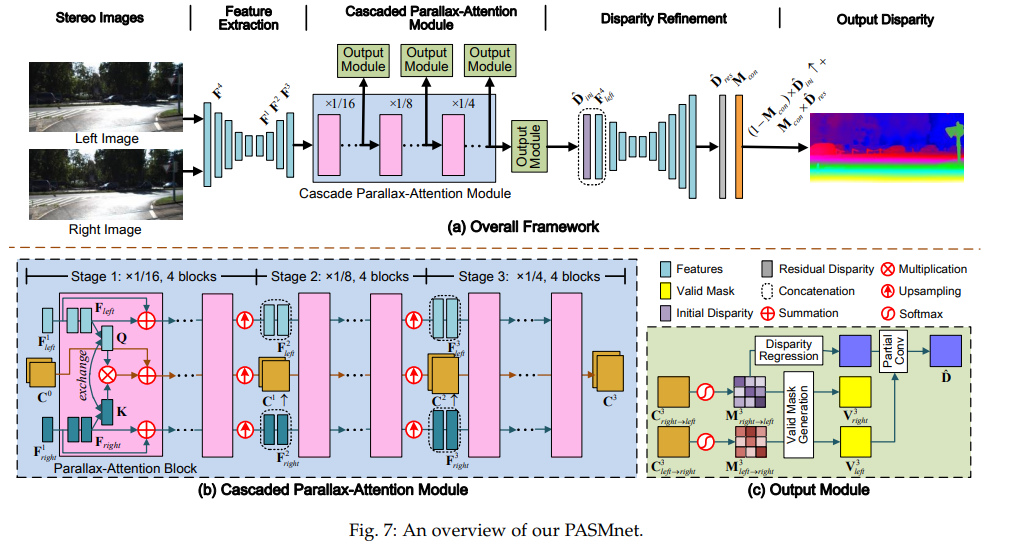
Cascaded Parallax-Attention Module
먼저 stereo image pair는 파라미터를 공유하는 Hour-glass network를 통해 feature를 추론합니다. 여기서 scale에 따른 feature를 이용하기 위해서 서로 다른 scale feature를 재활용하여 scale에 맞는 Cascaded Parallax-Attention Module에 concat 되어 활용되어 집니다.
Cascaded Parallax-Attention Module은 3 stage(1/16, 1/8, 1/4)에 4개의 Parallax-Attention Block으로 구성되어집니다. 각 블록은 앞에서 언급한 PARALLAX-ATTENTION MECHANISM과 동일하게 Key map과 Query map을 이용하여 Matching Cost(Parallax-attention map(left->right, right->left))를 획득합니다. 다른 점은 Parallax-attention map만 구하고, 양방향의 특징맵으로부터 3×3 conv을 적용합니다. 다음 stage에서는 Upsampling을 적용하여 coarse-to-fine한 방법을 가져갑니다.
Output Module
해당 모듈에서는 valid map과 disparity를 예측합니다. valid map(양방향)은 위에서 언급한 임계값을 이용하여 예측합니다.
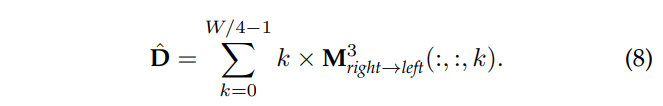
disparity를 추론하기 위해서 matching cost에 해당하는 후보들의 모든 weight를 합쳐 계산합니다. 이를 통해 disparity를 고정하지 않고 유연하게 예측이 가능해집니다.
Disparity Refinement
해당 모듈에서는 영상의 엣지와 같은 구조적인 정보를 활용합니다. 먼저 수식 8에서 예측된 디스패리티와 feature extraction의 앞쪽 layer에서 추출한 Feature map F_4과 concat하여 hourglass network에 태워 residual disparity map D_res과confidence map M_con을 획득합니다.
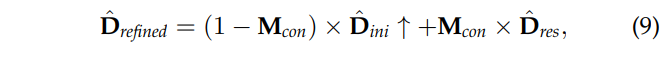
그 다음 수식 9를 이용하여 강화된 disparity map을 얻을 수 있습니다.
Loss
Photometric Loss
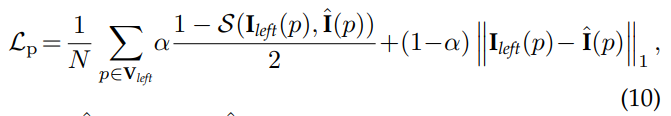
기존의 Photometric Loss와 동일하게 SSIM과 MAE를 이용하여 구합니다., p는 valid mask 중 1(non-occlusion)에 해당합니다.
Smoothness Loss
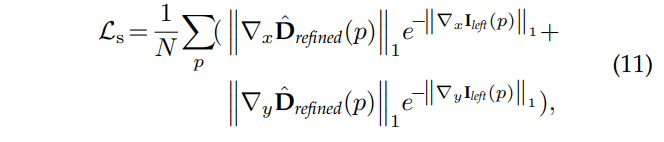
해당 로스 텀 또한 기존 loss와 동일하게 local smootheness를 강화합니다.
PAM Loss
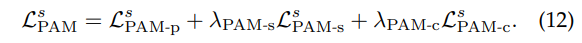
PAM Loss는 3 스테이지 별로 구해집니다.
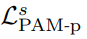
해당 로스는 photometric loss를 PAM에 맞도록 변형했습니다. 특히 parallax-attention map의 left-right consistency를 이용하여 loss를 구성합니다.
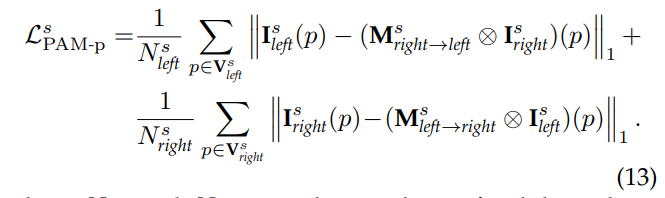
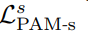
해당 로스는 smoothness loss를 변형합니다. 직접적으로 parallax-attention map에 규제를 가합니다.
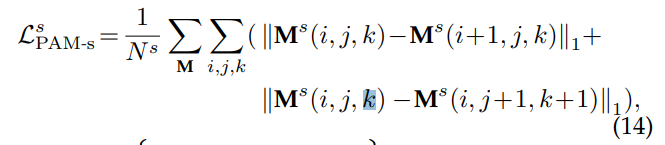
위의 수식을 통해 수평/수직 측명에서 유사성이 강화되도록 합니다.
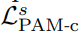
마지막으로 parallax-attention map의 cycle consistency를 이용합니다.
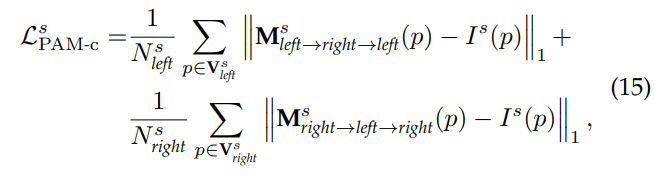
해당 로스는 수식 2에서 알게된 특성을 이용하여 cycle-attention map이 identity matrix와 같아야한다는 것을 이용합니다. 여기서 I는 identity matrix에 해당합니다.
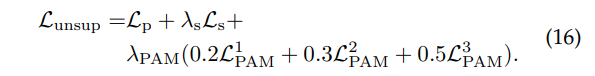
최종적으로 수식 16과 같이 loss를 계산하여 이용합니다.
Experiment
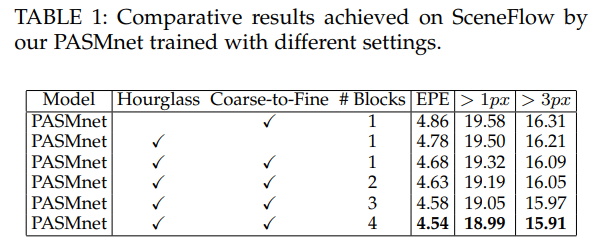
PASMnet에서 scale를 고려한 Hourglass network와 Coarse-to-Fine 방법의 영향을 성능 향상을 통해 볼 수 있습니다. palarax-attention block의 개수가 증가하며 성능이 향상되는 것을 통해 해당 모듈의 효과를 볼 수 있습니다.
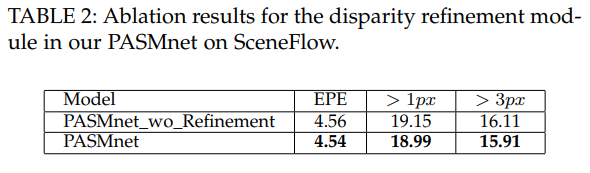
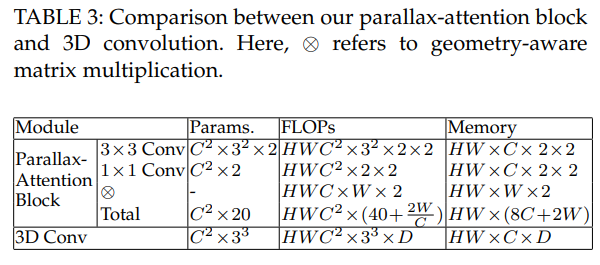
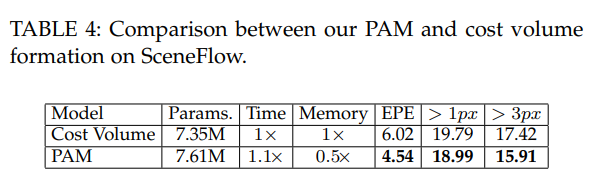
저자가 주장한 내용 중, 기존의 방법론 보다 적은 계산량이 든다고 했습니다. 해당 실험을 통해 기존 방법론들이 많이 사용하는 3D conv와 cost volume과 비교했을 경우, 상대적으로 매우 적은 계산량을 가진 것을 볼 수 있으며, 준수한 성능을 가진 것을 확인할 수 있습니다.

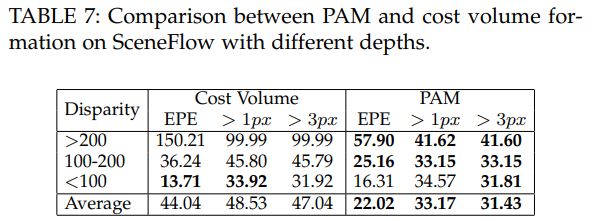
가장 중요한 실험에 해당하는 disparity range에 해당하는 실험입니다. 기존의 방법론에서는 범위 이상의 disparity가 주어질 경우, 성능이 급격하게 떨어지는 것에 반에 제안한 방법론은 어느정도 성능을 유지하는 것을 통해 제안한 모듈의 효과를 증명합니다.
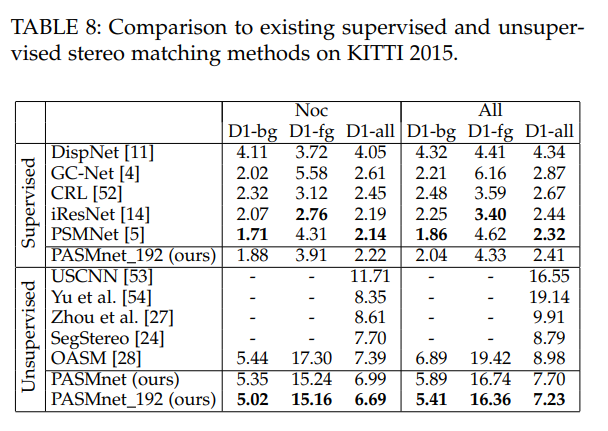
해당 실험에서 저자는 다른 방법론과 fair comparison을 위해 다른 방법론(비지도 학습)과 동일하게 disparity를 192로 범위를 지정했다고 합니다… 다른 지도 학습과 비교를 위해 지도 학습을 진행하여 비교를 했습니다. 결과적으로 비지도 학습에서는 다른 방법론보다 좋은 성능을 보이며, 지도 학습 방법론을 적용했을 떄도 기존의 방법론과 작은 차이를 보여줍니다.
END======================
해당 방법론은 기존의 트렌드인 방법과는 다른 연구 방향성을 제시 하였으며, 실용적인 측면에서 고질적인 문제인 disparity range에 대해 태클을 걸고 해결책을 제시하고 상대적으로 GT를 얻기 힘든 depth task에서 비지도 학습을 제안한 논문이다. 역시 이정도는 되어야 TPAMI에 올라가나 보다.
그리고 MTN에서는 R-T간 생성된 영상으로 cycle concistency 구하는 방법을 사용하였다. R-T 간 feature의 유사도를 계산이 가능하도록 feature engineering 학습한 후 해당 방법을 적용한다면 향상된 성능을 가진 스테레오 매칭 방법론을 제안할 수 있다는 가능성이 있다고 생각한다.