이번 리뷰 논문은 end-to-end의 Stereo Depth estimation에 대한 방법론이며, NeurlPS에서 Spotlite를 받은 페이퍼에 해당합니다. 매칭에 대한 모호함(e.g. 물체의 경계)을 해결하기 위해 offset 모듈과 Wasserstein Distances loss를 제안합니다. 또한 스테레오 매칭과 3D Object Detection에 대한 평가를 진행하였습니다.
Motive
단안 깊이 예측과 달리 스테레오 깊이 예측은 매칭된 두 픽셀로부터의 ray가 겹쳐지는 부분을 통해 3D point의 scale 모호성을 해결할 수 있는 장점을 있습니다. 또한 대응되는 모든 픽셀 쌍간의 거리(Disparity)와 두 카메라 사이의 거리(Baseline)에서의 삼각 측량 방법으로 깊이 정보를 추론할 수 있기에 LiDAR보다 dense한 깊이 정보를 가져올 수 있습니다. 하지만 픽셀간 잘못된 매칭이 발생할 경우, 정확성을 대폭 떨어뜨릴 수 있다는 단점이 있습니다. 픽셀 매칭은 조도 문제, 시점 차이로 발생하는 물체의 모양 변화 혹은 가려짐 문제, 물체 혹은 카메라의 빠른 움직임으로 인한 블러 등이 존재합니다. 이와 같은 문제들은 CNN의 발전으로 전통적인 기법에 비해 강인한 성능을 가져왔습니다.
학습 기반의 Stereo Depth estimation 또한 CNN을 이용합니다. CNN으로부터 두 영상에서의 매칭되는 픽셀별 Disparity value d(d /in {0,1,…,190,191})에 대한 categorical probability distribution S_disp을 예측합니다.

가장 나이브한 방법으로는 위의 수식처럼 모든 픽셀에서의 categorical distribution을 구해 argmax를 적용하여 매칭되는 픽셀쌍을 찾을 수 있습니다. 하지만 이 방법을 사용한다면 예측되는 disparity는 정수 타입을 가진 값만 가지게 됩니다. 정수 값을 이용할 경우, 표현 가능한 깊이의 범위가 줄어드는 한계가 존재합니다. 정수의 한계를 극복하기 위해 연속적인 값을 가지도록 아래와 같이 weighted combination(i.e. mean)을 이용하여 disparity를 예측하는 방식을 사용합니다.
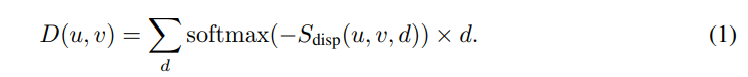
+ 해당 수식이 왜 mean을 의미하는지 이해가 안가시는 분들은 기댓값(wikipedia)에 대한 수식을 상기해보신다면 이해가 갈겁니다.
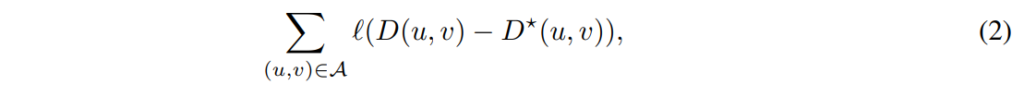
학습 기반의 방법론들은 영상의 feature extractor와 3d conv 추론하여 위의 수식 2와 같이 disparity error를 최소화하는 방식을 이용합니다. 최근 방법론으로는 disparity 대신에 depth를 직접적으로 예측하는 방식을 사용합니다. 해당 방법론에서는 disparity estimation에 주로 다룹니다.
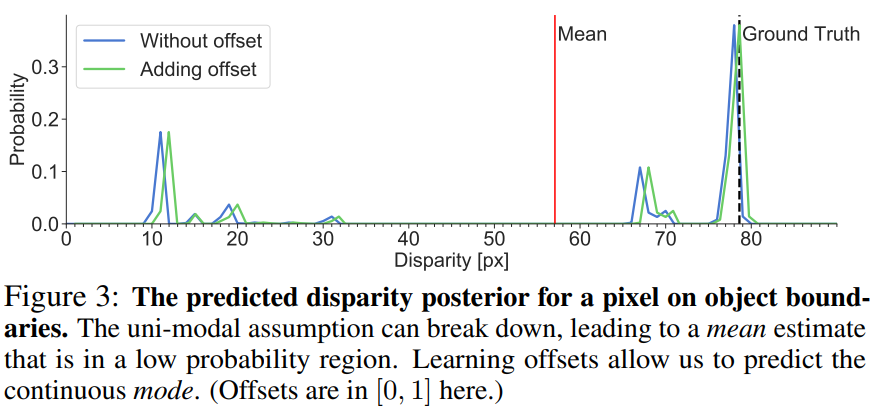
위에서 설명한 것과 같이 기존의 방법론들은 Fig 3와 같이 mean 값을 이용하여 정수가 아닌 예측된 정보들(disparity value 별 확률 값, mode)의 연속성이 고려된 float 값을 disparity를 가져감으로써, 보다 상세한 깊이 정보를 예측할 수 있습니다. 하지만 Fig 3에서 보여주는 것처럼 Mean과 GT가 가깝지 않은 경우가 생깁니다. 특히 물체의 경계선에서 fig 3과 같은 문제가 많이 발생합니다. 예를 들자면 배경이 하늘인 10m 거리에 위치한 차량 촬영된 영상이 있다고 가정하고, 차량의 경계선으로부터 매칭 픽셀을 찾는다고 가정합니다. 이상적인 결과는 예측을 위한 픽셀과 동일하게 다른 시점의 영상에서 차량의 경계선에 해당하는 픽셀을 찾아야합니다. fig 3을 빗대어 설명하자면 GT의 위치, disparity 80px에서의 대응 픽셀을 매칭해야합니다. 하지만 mean 값을 사용하는 최신 방법론들은 fig 3과 같이 다른 pixel을 매칭쌍으로 추정하고 최악인 경우 하늘을 매칭 픽셀로 추정하게 됩니다. 이로 인한여 모호한 지역인 경우 실제와 일치하지 않는 부정확한 추정이 발생할 수 있습니다.
다른 문제점은 수식 2와 같이 모델은 확률 분포에 대한 기대값을 이용하여 학습이 되기 때문에 실제 예측 값인 확률 분포을 직접적인 학습을 보장할 수 없다는 것에 있습니다.
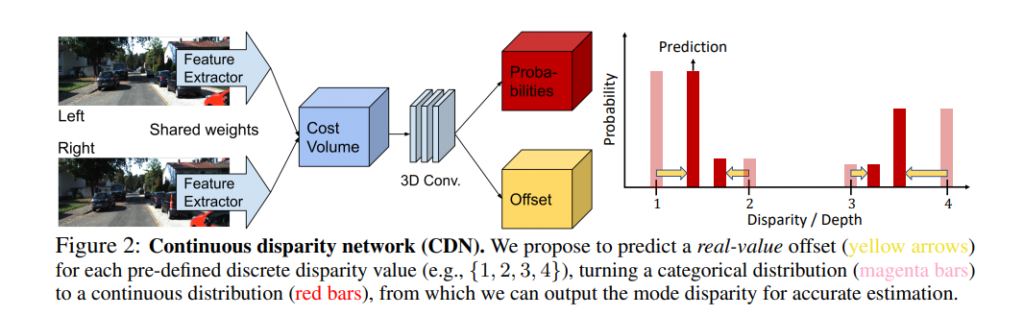
이러한 기존의 학습 기반의 방법론에 대해 문제를 해결하기 위해 Fig 2와 같이 categorical probability distribution에 대한 mode를 shift시켜 직접적으로 GT의 차이를 최소화하는 offset에 대한 모듈과 distribution을 GT에 유사하도록하는 Wasserstein Distances loss를 제안합니다.
Method
Continuous disparity network (CDN)
기존의 방법론들은 수식 1과 같이 확률 분포에 대한 mode들은 정수 형태를 가지는 문제가 있습니다. 해당 방법론에서는 연속적인 형태를 가져가기 위해서 아래와 같은 수식을 가진 softmax를 사용합니다.
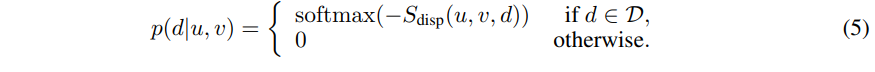
그리고 fig 2의 ‘Offset’에 해당하는 sub-network b(u, v, d)를 제안합니다. 정수 형태의 disparity value d에 대한 offset을 주는 예측하는 역할을 하며 수식은 아래와 같습니다.
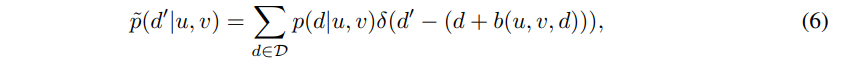
+ 수식 6에 대해서 쉽게 풀어서 설명하자면, 확률 분포 값들을 d에서 d’로 이동 시키기 위한 수식입니다.(보다 자세하게 이해하기 위해서는 dirac delta function이 뭔지 이해를 해야합니다. 간단한 설명으로는 0에 가까운 값은 1 그외의 값은 0을 내보내는 함수로 이해하시면 될 것 같습니다.) 지금 수식에서 d’=d+b(u, v, d)에 해당합니다. 즉 이전에 위치에 해당하는 d에서만 d’ – (d+b(u, v, d))는 0을 가집니다. 이때 디랙 델타 함수가 1을 가지고 이외에는 0이기에 이전 d에서 d’로 p을 옮기는 수식에 해당합니다.
해당 네트워크는 고정된 d를 offset을 통해 보정하는 것은 bbox를 offset으로 보정하는 one-stage object detection과 유사하게 디자인 됩니다. sub-network b(u, v, d)는 S_disp와 공유된 conv에서 fc 통해 학습/추론이 됩니다.
Learning with Wasserstein distances
============================================================================
+ Wasserstein distances??
해당 섹션에 대해 설명하기전에 Wasserstein distances이 뭔지에 대해 설명을 드리겠습니다. 딱히 필요없다고 생각하시면 다음 파트로 셀로 넘어가시면 됩니다.
해당 기법은 확률 분포 간의 차이를 측정하는 방법 중 하나입니다. 해당 방법외에도 확률 분포의 차이를 측정하는 방법에는 KL divergence가 있습니다. KL은 두 확률 분포의 엔트로피의 차이를 계산하는 방법론이며, 이를 거리 값으로 활용하기 위해서 사용하는 Jensen-Shannon divergence(JSD)~1/2KL(p||M)+1/2KL(q||M), M=(p+q)/2가 있습니다. 엔트로피를 이용한 방법들은 각 확률 분포의 기댓값에 대한 차이라고 근사가 가능합니다.
이러한 방법론과는 다르게 Wasserstein distances는 두 확률 분포를 유사하게 만들기 위해서 이동시켜야하는 횟수 x 이동 거리를 측정한 방법론입니다.
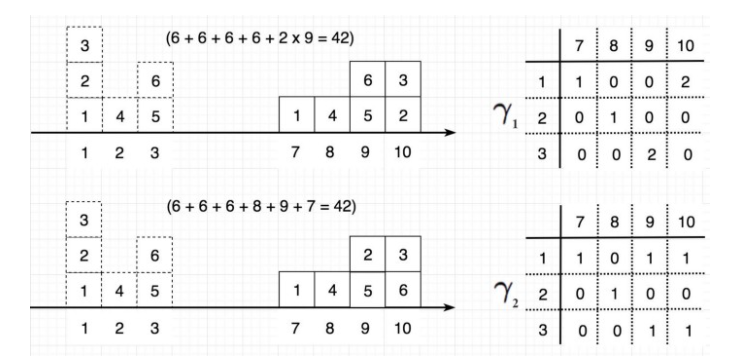
예를 들자면 위의 그림과 같이 1에 위치한 2개의 값을 10으로 옮기다면 r_1과 같이 (1,10) = 2 할당하는 식으로 표현이 가능합니다. 그리고 각 위치에 대한 이동 거리를 다 더하는 방법에 해당합니다. 위의 그림처럼 다양한 형태가 구성될 수 있습니다.
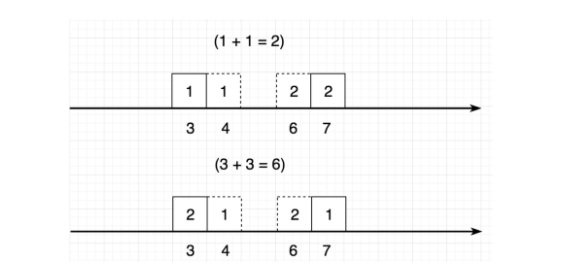
하지만 위의 그림처럼 항상 같은 거리가 나오는 것은 아닙니다. Wasserstein distances 는 코스트를 최소화하여 분포 p를 q로 이동시키는 것이라고 생각하시면 됩니다. 이를 수식화 하면 아래와 같습니다.
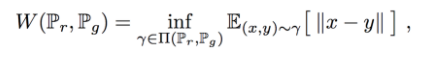
+ 여기서 inf는 상한(infimum)을 의미합니다.
해당 기법은 KL, JSD와는 다르게 확률 분포의 기하 정보가 고려된 거리 측정 법이라고 보시면 될 것 같습니다.
====================================================================
위 섹션을 통해 offset을 이용하여 분포의 위치를 조절하는 방법에 대해 소개하였습니다. 해당 섹션에서는 GT와 추론 분포 간의 차이를 계산함으로써 offset과 disparity에 대한 categorical distribution을 예측하는 Loss에 대해 소개합니다. 효과적으로 분포를 유지하기 위해 기하적인 Wasserstein-p distances 를 이용한 Loss를 제안합니다.
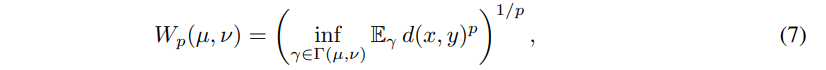
확률 분포 µ를 ν로 변화 시키기 위한 x에서 y의 이동 거리에 해당합니다. 위의 값들 p의 의미는 멱평균의 파라미터에 해당합니다. 수식 7을 GT가 존재하는 수식으로 변경하자면 아래와 같은 수식으로 간단하게 변경이 가능합니다.
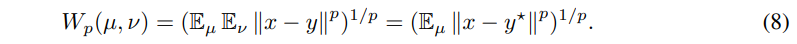
다시 수식을 offset이 적용된 d’에 관한 수식으로 변경한다면
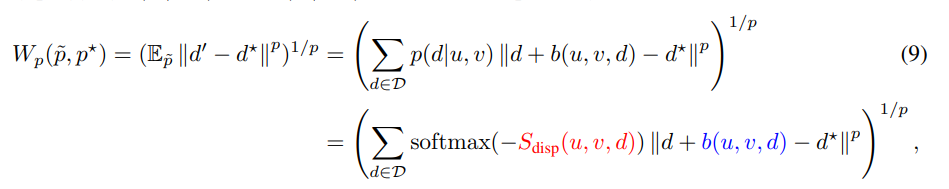
수식 9와 같이 간단하게 표현이 가능합니다. 빨간 색은 conventional disparity network을 학습이 가능한 부분이며, 파란색은 sub-network를 학습 가능합니다. 해당 방법론에서는 p는 1과 2를 이용하여 거리값을 구합니다.
Extension: learning with multi-modal ground truths
위 섹션에서 분포의 형태를 고려하여 offset과 S_disp를 예측하는 loss에 대해 소개하였습니다. 하지만 GT는 분포 형태가 아닌 단일 값이기에 직접적으로 분포 형태를 학습하는 것이 아닌, disparity를 통해 학습하도록 기대를 해야합니다. 저자는 보다 직접적으로 분포를 학습하기 위해서 multi-modal GT, 즉 분포 형태로 변화시키는 부분을 소개합니다.
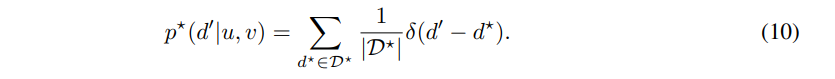
수식 10은 수식 6과 동일한 목적으로 우치를 d의 범위를 변경시키고 분포 형태로 변경시켜주는 핵심 부분입니다.
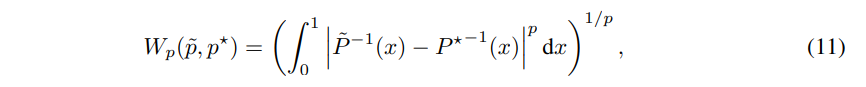
이를 수식 8에 대입한다면 수식 11과 같습니다.
(+여기서 P는 누적 분포 함수라고 하는데 왜 역함수가 붙었는지는 모르겠습니다. 추후 이해하게 된다면 추가 하도록 하겠습니다.)
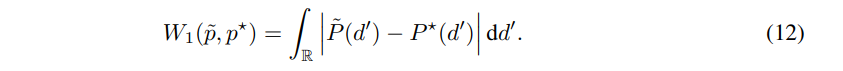
이를 p=1를 이용한다면 다음과 같이 간단하게 표현이 가능하며, 보다 효율적인 계산이 가능해집니다.
Experiments
실험은 Stereo disparity/depth은 Scene Flow, 3D object detection과 depth는 KITTI를 이용하여 평가하였습니다.
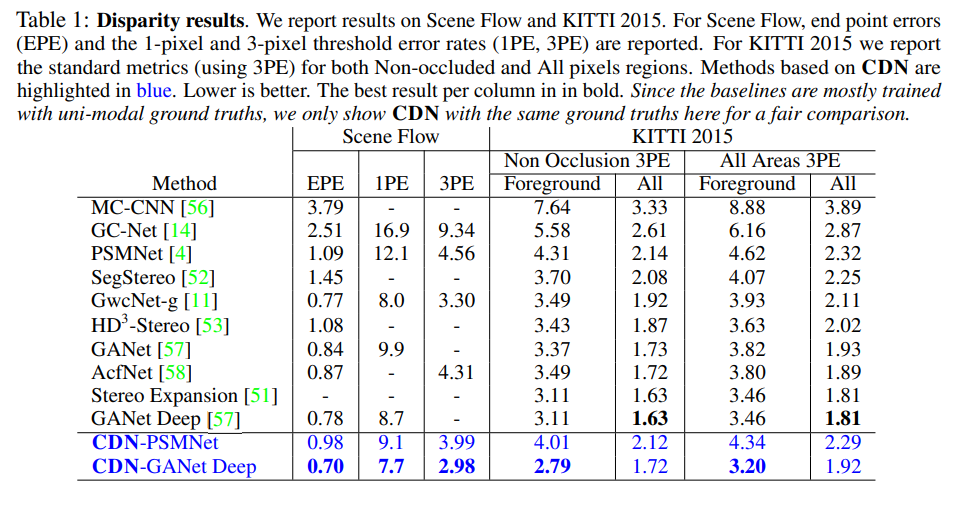
1PE 및 3PE로 표시된 1픽셀 및 3픽셀 임계값 오류를 사용합니다. PE는 큰 격차 오차를 가진 특이치에 강한 반면, EPE는 오류를 하위 픽셀 수준으로 측정합니다.
해당 방법론의 장점은 Table 1에서처럼 기존의 방법론에 적용이 용이하다는 점도 있습니다. 대부분의 실험은 기존의 방법론에 추가되어 실험이 진행되어졌습니다. 기존의 방법론에서 향상된 성능을 가지고 온 것을 확인 할 수 있습니다.
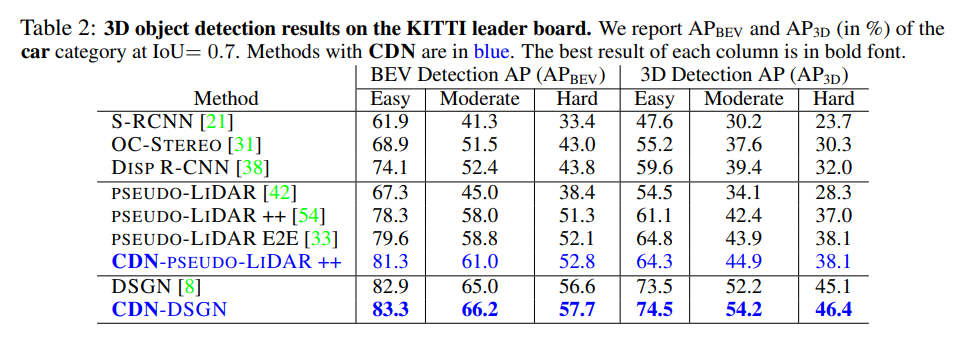
또한 추정된 Depth를 pseudo-lidar로 변형하여 3d object detection에 대한 실험을 진행하였습니다. 해당 방법론은 경계 부분의 모호성에 집중하였기에 물체의 경계면이 중요한 3d object detection에서도 성능향상을 가져온 것 을 확인 할 수 있습니다. 기존의 영상 기반 방법론보다 좋은 성능을 가져옵니다.

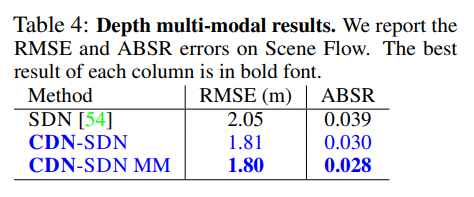
기존 방벙론에서 해당 방법론을 적용시 성능 향상을 보여줍니다. 여기서 MM은 GT를 Multi-Modal로 변경하여 학습한 부분에 해당합니다.
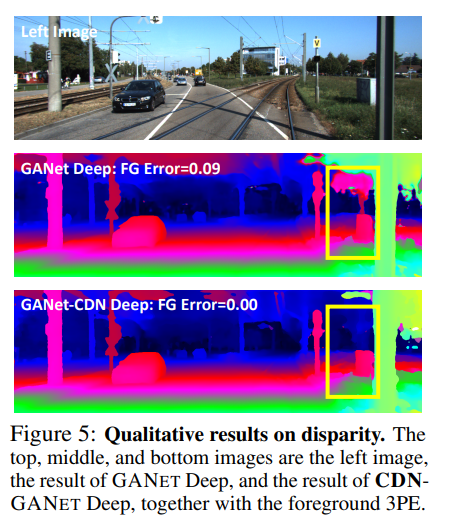
fig 5의 노란색 박스를 통해 경계면에 대해서 강인함을 보여줍니다.
==========================================================================
이번 리뷰 논문은 명확한 모티브와 그에 대한 해결책인 방법론을 제시합니다. spotlite를 받는 논문은 확실히 이유가 있는 것 같습니다. 논문은 이전의 방법론에 대해서도 설명과 간단한 수학식을 통해 명확하게 설명해주며 방법론에 대한 뒷받침 또한 명확하며, 정석적 정량적 결과물 또한 임팩트가 있었습니다.
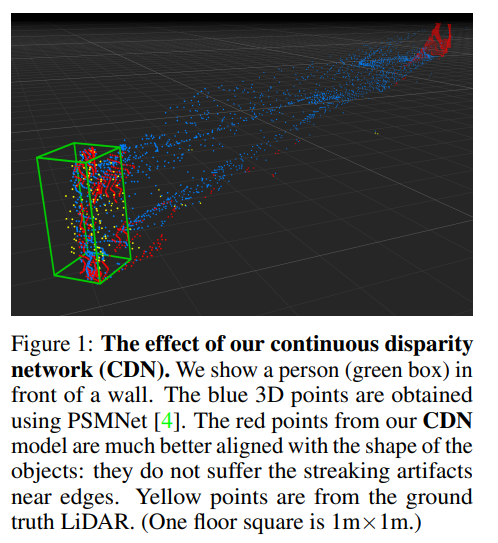
또한 Fig 1과 같이 이전의 방법론과 해당 방법론의 효과를 Pseudo-lidar로 표현한 부분은 정말 명확하게 장점을 잘 표현하는 것 같습니다. (Red : CDN, Blue : previous work, Yellow : LiDAR) 해당 방법론은 pseudo-lidar 기반의 연구들에 대해 방향성을 잘 잡아준 논문이라고 생각하며, 3d에 대한 연구를 위해서는 지속적으로 후속 연구들에 귀 기울여 봐야겠다는 생각이 듭니다.
Disparity 성능 비교 실험 테이블에서 전통적인 Disparity 계산 방식의 성능은 stereo expansion 부분을 보면 될까요?
혹은 stereo expansion이 딥러닝 기반 알고리즘이라면 논문에서 제안하는 방법론과 전통적인 알고리즘과의 차이는 어느정도 나는지에 대한 설명이 있다면 알려주시면 감사하겠습니다.
Stereo expansion [1]은 딥러닝을 이용한 방법입니다. 자세한 내용은 아래 인용문을 참고 바랍니다.
최신 Object detection 혹은 Classification에서 전통적인 기법과 성능을 비교하지 않는 것과 동일하게 해당 task에서도 비교하지 않습니다.
[1] Yang, Gengshan, and Deva Ramanan. “Upgrading optical flow to 3d scene flow through optical expansion.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.