transformer 공부를 해볼겸, 가장 시초가 되는 논문에 대하여 리뷰를 하고자 합니다.
Introduction
일단 transformer는 NLP 분야에서 제안된 방법론입니다. 특히 NLP분야 중에서도 번역 분야로 처음 제안되는 걸로 알고 있는데, 애초에 NLP 분야에 대해서는 잘 알지 못해서 간략하게만 정리하고 넘어가겠습니다.
transformer가 나오기 전에는 RNN기반 encoder와 decoder를 사용했다고 합니다. 예를 들어 “오늘 날씨가 흐리다.” 라는 문장을 모델의 입력으로 넣으면 문장 속 각 단어들이 하나의 벡터로 인코딩이 된 다음 이러한 벡터들을 문장의 끝에 올 때까지 디코딩을 통과하여 번역된 문장 “It’s cloudy today.” 이 나오게 됩니다.
간단한 문장정도는 기본적인 RNN 모델로도 충분히 학습되어 사용할 수 있겠지만, 책과 같이 매우 긴 문장의 경우에는 다양한 단어들이 나오므로 특정 단어들끼리 밀접한 관련이 있는지 없는지 등을 분석하기가 매우 어려워집니다.
그리하여 attention 기법을 추가로 사용하는 RNN 방법론들이 제안되었으며, 이러한 기법덕분에 긴 문장에서도 효과적으로 번역을 수행할 수 있다고 합니다. 하지만 RNN방법론 자체가 문장 속 단어들을 순차적으로 보기 때문에 속도적 측면에서 단점이 존재하였으며 성능도 무언가 아쉬웠습니다.
그렇게 하여 제안된게 바로 transformer입니다. transformer는 sequence-aligned RNN(or CNN)을 사용하지 않아 속도적 측면에서 기존보다 더 빠르면서도 transformer에서 제안하는 attention 방법론 덕분에 매우 우수한 성능까지 보장합니다.
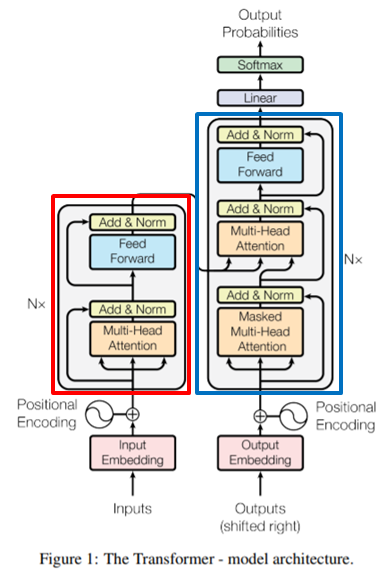
모델의 전체적인 구조는 그림1과 같습니다. 붉은 색 박스에 해당하는 부분이 encoder이며, 파란색 박스에 해당하는 부분이 decoder입니다. 얼핏보면 인코더와 디코더가 하나씩 존재하는 것 같아 보이지만, 실제로는 총 6개씩 존재한다고 합니다(각 박스의 왼쪽과 오른쪽에 N\times가 있죠? N이 6입니다.)
Encoder
일단 인코더 내부를 살펴보시면, Multi-Head Attention이라는 layer와 Feed Forward layer가 존재합니다. Multi-Head Attention은 단순히 attention layer로 볼 수 있는데, 인코더가 입력 문장 내 다른 단어들을 효과적으로 볼 수 있게끔 도와줍니다.
이러한 attention layer로부터 나온 output을 feed forward layer의 입력으로 사용하게 되며 중간중간에 residual 방식으로 합쳐지고 normalization 과정을 진행하게 됩니다.
Self-Attention
Attention layer에 대해서 더 자세히 알아보겠습니다. 먼저 해당 레이어의 입력으로는 문장을 단어로 쪼갠 다음, 각 단어를 벡터화시킨 벡터를 입력으로 사용합니다.

각 단어 벡터의 크기는 512이며, 당연하다시피 맨 처음의 인코더 입력에서만 벡터 임베딩을 진행하고 그 다음에는 하나의 인코더에서 나온 출력을 그대로 다음 인코더의 입력으로 사용합니다. 이때 2번째 인코더의 입력도 역시 512 크기의 벡터를 사용하게 됩니다.(단어 벡터의 크기는 하이퍼파라미터입니다.)
그리고 각각의 단어 벡터들로부터 Query, Key, Value 벡터들을 생성합니다. 각각의 벡터들을 생성하는 방법은 매우 단순합니다. 그냥 학습과정에서 3가지 종류의 weighted matrix를 단어 벡터에 곱해줌으로써 만들 수 있습니다. 이때 각각의 weighted matrix는 우리가 학습해야할 값입니다.
그 다음으로는 스코어를 계산합니다. 이게 무슨 말인가하면, self-attention을 하기 위해서 문장 속 하나의 단어와 그 외에 다른 단어들(자신 포함)끼리에 대하여 각각의 점수들을 모두 계산하는 것입니다. 즉 해당 단어와 제일 밀접한 관련이 있는 단어가 무엇인가를 스코어로 표현하는 것이죠.
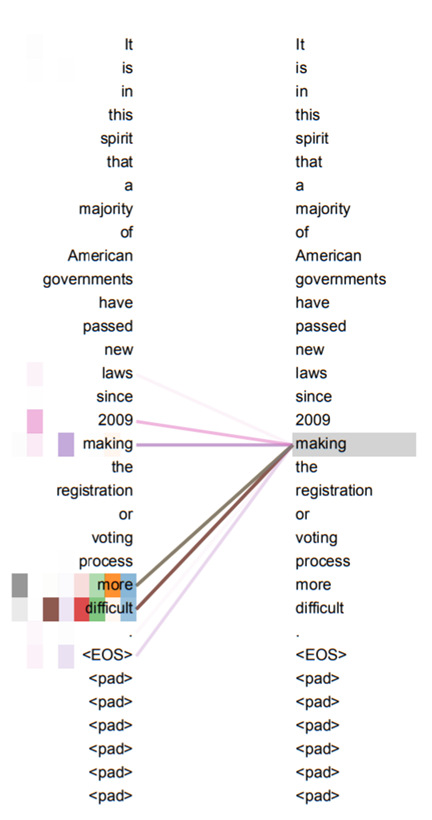
self-attention에 대한 위에 내용의 이해를 돕기 위해 그림3을 살펴봅시다. 그림3은 self-attention에 대하여 시각화하여 표현한 것입니다. It is in this … more difficult까지 긴 문장이 존재하는데, 이 문장 내에서 각 단어들끼리 얼마나 연관성을 가지고 있는지를 보기 위하여 각 단어들끼리 점수를 계산하는 것이지요.
그림3의 예시에서는 making이라는 단어를 인코딩하기 위해서 물론 입력 문장의 making도 영향력을 끼치긴 했지만 그 외에 more difficult라는 단어들이 영향력을 행사하는 모습을 볼 수 있습니다.
즉 self-attention은 모델이 입력 문장 속에서 다른 위치에 존재하는 단어들을 참고하여 현재 인코딩하고자 하는 위치의 단어를 더 정확히 인코딩한다고 보시면 될 것 같습니다.
다시 transformer로 돌아와서, 모델이 self-attention을 수행하기 위해서는 현재의 단어와 그 외의 단어들끼리의 연관성을 나타내는 스코어가 필요하다고 했었습니다. 각 단어별로 점수를 계산하는 방법은 간단합니다. 바로 해당 단어 벡터들의 query vector와 key vector를 내적해주면 됩니다.
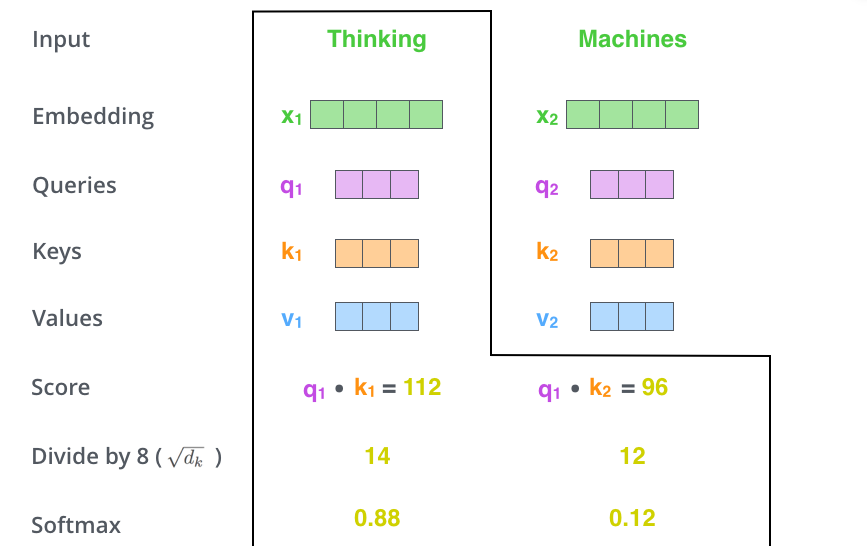
그림4를 보시면 쉽게 이해하실 수 있는데, 만약 입력 문장 속에 Thinking과 Machines라는 단어가 존재한다고 해봅시다. 그럼 해당 단어를 임베딩하여 512크기의 벡터로 만들어준다음, 3종류의 weighted vector를 곱해줌으로써 각 단어의 query, key, value vector를 형성합니다.
그리고 나서 attention을 하기 위하여 각 단어별로 score를 계산하는데, 이때 Thinking과 Thinking에 대한 score는 q_{1} \dot k_{1}으로 구할 수 있으며, Thinking과 Machine에 대한 score는 q_{1} \dot k_{2}로 계산할 수 있습니다.
만약 문장 속 단어가 n개가 존재한다면 쭉쭉 계산하여 q_{1} \dot k_{n}까지 계산하게 되겠죠?
그렇게 계산된 각 단어의 스코어에 대해서 8로 나누어주게 됩니다. 여기서 갑자기 웬 8로 나누지라고 하실 수 있는데, 이 8은 key 벡터의 사이즈인 64의 제곱근을 의미합니다. 이렇게 key 벡터 크기의 제곱근으로 나누어주는 이유는 학습할 때 gradient를 안정화시켜주기 위함이라고 합니다.
마지막으로 각각의 스코어들에 대하여 softmax를 진행해주게 되면 target 단어에 대하여 자신포함 문장 내 다른 단어들이 얼마나 관련있는지를 확률적으로 표현할 수 있게 됩니다.
softmax까지 마친 스코어값을 해당 단어의 value vector에 곱해주게 되는데, 이를 통하여 관련 없는 단어들은 스코어가 작은 값으로 곱해짐으로써 0에 가까운, 의미없는 값으로 나타날 것이며 관련이 있는 단어 벡터들은 1에 가까운 값들이 곱해짐으로써 이전값을 유지할 수 있게 됩니다.
마지막으로 스코어 값들이 곱해진 weighted value 벡터들을 모두 다 합해주면 self-attention layer의 최종 출력값을 구할 수 있게 됩니다.
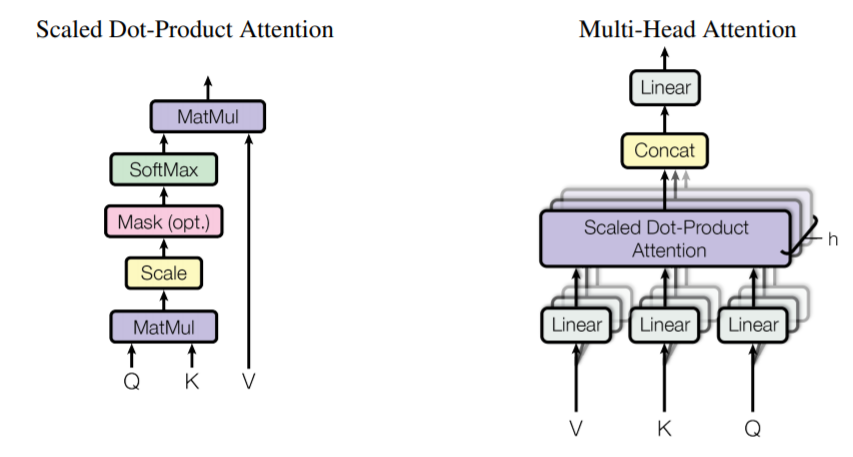
자 위에 설명은 그저 벡터에 대한 연산으로 설명을 진행했었죠? 하지만 각각의 단어들에 대해서 일일히 벡터로 계산하면 번거롭고 시간낭비입니다. 그래서 문장 속 단어 벡터들을 착착 쌓아서 행렬로 만든다음 위의 attention 과정을 진행하게 되며 아래 수식처럼 표현할 수 있게 됩니다.
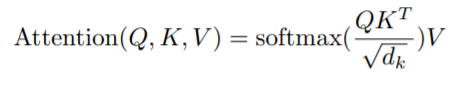
Q, K, V, \sqrt(d_{k})는 각각 Query, Key, Value vector들을 모두 packing하여 만든 행렬들과 key matrix 크기의 제곱근을 나타낸 것입니다. 각각의 행렬들은 역시나 단어벡터를 packing한 단어 행렬에다가 learnable weighted matrix를 곱해주면 만들 수 있겠죠?
Multi-head Attention
지금까지 알아본 내용은 단일 self-attention에 대해서 알아본 것입니다. 하지만 transformer에서는 multi-head attention 기법을 사용하여 더욱 성능을 향상시켰습니다.
Multi-head attention을 하는 이유에 대해서 먼저 알아봅시다. 해당 방식ad attention을 하는 이유에 대해서 먼저 알아봅시다.
가장 큰 이유는 바로 attention을 할 때 multi head를 사용하면 다른 단어들을 더 잘 볼 수 있기 때문입니다. 예를 들어 single head attention의 경우에는, 비록 score를 계산하면서 연관성이 있어 보이는 단어들에게도 높은 점수를 주겠지만 대부분은 자기 자신의 점수(위에 예시로 따지면 q_{1} \dot k_{1})를 높게 주려고 할 것 입니다.
하지만 8개의 multi head로 구성되어 있으면, 각각의 head 마다 서로 다른 weighted (random init) matrix를 통해 서로 다른 score들이 계산됨으로써 모델이 현재 단어 외에 다른 위치의 단어에 집중하는 능력을 확장시킬 수 있습니다.
또한 추가적으로 multi head를 사용하는 attention layer를 통해 생성된 벡터들은 서로 다른 representation space에 존재하게 됩니다. 논문에서는 각 벡터들이 서로 다른 representation space 존재함으로써 얻는 이점에 대해서는 언급이 없지만, 제가 생각하기에는 representation space가 늘어난다는 것은 벡터들의 표현 가능성이 더 늘어나니깐 학습에 더 좋은 영향을 준다는게 아닐까 싶습니다.
Multi-head attention 방법은 매우 간단합니다. 그냥 self attention 과정을 병렬적으로 진행하는 것입니다. self attention 과정에서 query, key, value를 만들기 위해 단어 벡터(행렬)에 learnable weighted vector(matrix)를 곱해주었었죠?
이 learnable weighted vector(matrix)는 랜덤하게 initial 되었기에 병렬적으로 동시에 진행하게 되면 각각의 attention layer에서 서로 다른 attention output을 생성할 것입니다. 이렇게 생성된 결과를 z_{n}라고 하겠습니다.
그럼 z_{1}, z_{2}, ..., z_{n}까지의 결과를 concat한 다음, 마지막으로 weighted matrix인 W0를 곱해버림으로써 입력 matrix와 동일한 크기의 output matrix를 만들어주며 (그렇게 하는 이유는, 모든 인코더의 입력 사이즈는 동일하기 때문입니다.) 이를 수식으로 표현하면 다음과 같습니다.

위에 self-attention~multi head attention 과정을 그림5에서 확인가능합니다.
글의 내용이 길어져서 일단 인코더까지만 내용을 끊고, 다음번 리뷰에 디코더 부분에 대하여 작성하도록 하겠습니다.
안녕하세요 정민님 좋은 리뷰 감사합니다.
self-attention에서 단어 벡터들의 쿼리(Query) 벡터와 키(Key) 벡터를 내적하여 score를 계산하여서 벡터 간의 유사도를 측정하고 두 벡터가 유사할수록 내적값이 크고, 다를수록 작아진다는 특징을 이용해서 어텐션 스코어(Attention Score)를 계산합니다. 이후에 소프트맥스를 적용하여 어텐션 가중치를 구하고 밸류 벡터(Value)를 곱하여 가중합을 계산하는 것으로 이해하였습니다. 이때 Key와 Value의 역할이 무엇인지 헷갈리는데 Key는 참조할 위치의 정보를 나타내고, Value는 해당 위치의 실제 단어 즉 Query와 비슷한 걸로 이해하면 될까요?
안녕하세요, 정민님 좋은 설명 감사드립니다.
제가 잘 모르지만 최대한 이해를 하고 질문을 드립니다
self-attention에서 Query와 Key의 내적을 통해 단어 간의 연관도를 계산하고, 이 점수를 기반으로 Value들을 가중합하여 최종 출력으로 사용하는 구조는 이해했습니다.
그런데 Query와 Key는 ‘얼마나 관련 있는지’를 판단하기 위한 기준이라면, 결국 모델이 어떤 단어에 더 집중할지를 결정하는 역할이고, Value는 그 집중의 결과로 가져올 “실제 정보”를 담고 있다고 이해했습니다.
그렇다면 Query와 Key는 서로 다른 representation을 가져야 하는 이유가 무엇일까요?
둘 다 input에서 동일한 정보로부터 생성되는데, 굳이 각각 다른 weight matrix를 통해 생성하는 구조를 선택한 이유가 있을까요?