[NIPS 2014] Generative Adversarial Network

Before Review

오늘 리뷰할 Paper는 그 유명한 GAN 입니다.

주워듣기만 하다가 논문이랑 관련 자료들을 참고해서 GAN에 대해 나름대로 공부를하고 정리를 해보려고 합니다.

읽으면서 정말 간단하면서도 명료한 아이디어에 감탄하게 됐고 , 수식 또한 어렵지는 않아서(수렴성 증명하는 부분은 빼고..) 전반적으로 이해하는데는 어려움이 없었습니다.

여담으로 GAN의 탄생 배경에 대해 조금 알아봤는데 당시에도 인간의 뇌를 흉내낸 신경망을 이용해 그럴듯한 데이터를 스스로 만드는 생성적 모델을 사용하고 있었지만 성능은 그리 좋지 않았다고 합니다.

복잡한 통계적 분석 기법을 각 요소들에 적용하는 방법들이 고려되고 있었는데 이는 수많은 계산이 필요한 일이였고 , 저자인 이안 굿펠로우는 이러한 방법이 좋지 않은 접근이라 생각하고 있었습니다.

맥주를 마시며 이 문제를 고민하던 이안 굿 펠로우는 마침내 “두개의 신경망을 서로 경쟁하면 어떨까” 라는 아이디어가 떠올랐고 집에 돌아온 후 몇시간동안 코딩을 한 결과 GAN이라는 멋진 결과가 나왔다고 합니다.(천재인듯 합니다..)

이렇게 2014년에 GAN이 세상에 등장한 이후 정말 많은 후속연구가 파생되었는데 오늘 그 시초가 되었던 GAN에 대해 review 해보겠습니다.

Introduction

사실 , GAN이 나오기 전에도 Generative Model들이 존재했지만 , GAN이 지금까지도 각광받는 이유는 적대적 생성 모델이기 때문인 것 같습니다.

적대적이란 말을 설명하기전에 우선 Generative Adversarial Network에 존재하는 두가지 network를 간단히 소개하겠습니다.

• Generative Model
  • 우리가 Input 으로 넣어준 Data(image, voice, text)의 distribution을 알아내려고 노력하는 network 입니다.
  • 이 Generator가 Data의 distribution을 잘 학습 했다면 학습한 distribution과 noise vector를 섞어줘서 그럴듯한 생성 data instance를 만들어 줄 수 있습니다.
• Discriminative Model
  • 입력으로 들어온 sample data가 진짜 input data로 부터 온 것인지 Generator로 부터 온 것인지를 구별하여 각각의 경우에 대한 확률을 estimate 합니다.
  • 입력으로 들어온 sample data가 Discriminator가 판단하기에 real data에 가까운 것 같다면 확률값은 1 , fake data에 가까운 것 같다면 확률값은 0 이런식으로 반환합니다.
  • 즉, 만들어진 가짜 데이터인지 진짜 입력 데이터로부터 온 것인지 구별하는 일을 하며 , 결과적으론 더 정교한 Generator를 만들기 위해 사용됩니다.

이를 가장 쉽게 설명해주는 예시가 위조 지폐범과 경찰인데 간단하게 말하면 위조지폐범(Generator)은 경찰의 눈을 피해 진짜 같은 위조지폐를 만들기 위해 노력하고 경찰(Discriminator)는 더욱 더 정교한 기법으로 지폐들을 검출하는 방향으로 노력합니다.

이것이 GAN의 핵심 아이디어 입니다.

결국 적대적 생성 모델이라는 것은 두개의 Network가 경쟁을 통해 정확해지고 이때 우리가 원하는 성능 좋은 Generator를 얻을 수 있습니다.

Generator 와 Discriminator의 Network를 본 Paper에서는 MultiLayer Perceptron으로 구현했고 후에 CNN이나 다른 network로 구현하는 많은 후속 연구가 나와있습니다.

Adversarial Network

이제 이 Adversarial Network가 어떻게 구성이 되는지에 대해 알아보겠습니다.

먼저 , 그럴듯한 데이터를 생성해주는 Generator부터 살펴보겠습니다.

Generator가 새로운 data instance를 생성하는 방식은 Generator가 학습한 distribution에 noise variable를 끼얹어서 만들어주는 방식입니다.

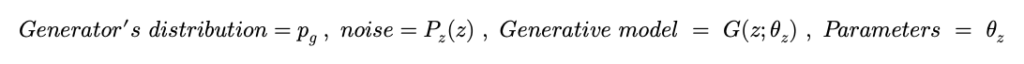
이때 , data instance를 만들어주는 것을 data space로의 mapping이라고 본 논문에서 표현하고 있는데 Generator distribution 에 noise를 섞어줘서 새로운 데이터를 만드는 것으로 이해하시면 되겠습니다.

Generator를 쉽게 G(z) 이렇게 표현하고 , 여기서 G는 미분이 가능하며 따라서 역전파를 수행할 수 있고 본 Paper에서는 Multilayer Perceptron으로 구성되어 있습니다.

다음으로 Discriminator를 알아보겠습니다. Discriminator 역시 Multilayer Perceptorn으로 구성되며 output은 하나의 scalar 값(확률)을 가집니다.

즉 , D(x)는 input으로 들어온 sample data(x)가 Generator가 아닌 data distribution으로 부터 왔을 확률을 나타냅니다.

introduction에서 알아본 것 처럼 Generator와 Discriminator는 서로 상반된 입장을 가지고 있습니다. 이러한 상항을 다음과 같은 Function으로 나타낼 수 있습니다.

V라는 loss function은 D와 G의 항으로 구성되어 있으며 어떤 Log값들의 Expectation 값들의 합으로 구성되어 있습니다.

함수를 이해하기 위해 서로의 입장에서 함수를 살펴보겠습니다 먼저 , Discriminator의 입장에서 loss function을 살펴보겠습니다.

• Discriminator의 입장

Discriminator는 data가 들어왔을 때 real data라면 자신있게 1을 외치고 싶을 것이고 , fake data라면 0을 외치고 싶을 것 입니다.

즉 , 최적의 Discriminator는 D(x)=1 , D(G(z))=0 이렇게 값을 가질 것입니다.

결국 D(x) , 1- D(G(z)) 값이 0 에서 1로 커지는 방향이 Discriminator 입장에서는 좋은 상황이며 , 이는 log(D(x)_{},_{}log(1-D(G(z))) 이 음의 무한대에서 0으로 가까이 가는 loss Function을 최대화 시키는 상황입니다.

• Generator의 입장

반대로 Generator는 Discriminator를 속이고 싶어합니다. 즉 D(G(z)) 값이 1이 되도록 만들고 싶어하는 녀석입니다. (사실 1까지는 아니고 0.5 정도로만 만드는 것이 목표입니다.)

만약 G(z)가 학습이 아예 안됐다고 가정해보면 , Discriminator 입장에서는 손쉽게 D(G(z))=0 이라고 결론 내릴 수 있습니다. D(G(z))=0 이라면 log(1-D(G(z))) 은 0의 값을 가지게 됩니다.

이제 G(z)가 학습이 충분하게 완료되어 real data distribution을 그대로 재현했다고 가정해봅시다. 이렇게 되면 Discriminator는 G(z)를 real data(x)라 착각하여 D(G(z))=1 의 값을 가지게 됩니다.

결국 1-D(G(z))값이 1 에서 0 으로 작아지는 방향이 Generator 입장에서는 좋은 상황이며 , 이는 log(1-D(G(z))) 이 0에서 음의 무한대로 발산하는 즉 ,loss Function을 최소화 시키는 상황입니다.

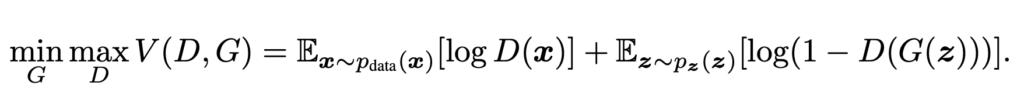
결국 이 V(D,G)라는 함수를 Discriminator는 최대화 시키는 방향으로 , Generator는 최소화 시키는 방향으로 학습이 진행되는 것을 알 수 있습니다.

학습의 과정을 간단하게 보여주는 그림입니다. (검은색 분포 : real data , 파란색 분포 : discriminator의 확률 분포)

noise variable z를 이용해 G(z)를 dataspace(x)로 mapping을 시켜주고 Generator distribution을 만들어줍니다(초록색).

초기에는 Generator가 real data distribution과 많이 다르기 때문에 discriminator가 generator와 real data를 잘 구분하여 비교적 큰 확률값을 가지고 있습니다.(구별을 잘 한다는 의미)

점차 학습이 진행되면서 Generator의 분포는 real data 분포와 비슷해지면서 최종적으로는 둘의 분포가 같아졌을 때 Discriminator는 0.5의 일정한 값을 가지고 있습니다.(x가 Generator로 부터 온것인지 real data인지 모르겠다는 의미)

GAN의 학습 알고리즘입니다. GAN이 가지고 있는 MinMax problem은 한쪽이 이득이 보면 한쪽이 손해를 보는 구조이기 때문에 두개의 네트워크를 동시에 학습시키지 않고 따로따로 학습을 시킵니다. 예를 들어 Discriminator를 먼저 학습시킨후 학습된 Discriminator를 가지고 Generator를 학습시키고 다시 이러한 과정을 반복하면서 학습하는 구조 입니다.

Discriminator는 Loss function을 최대화 시켜야 하므로 Gradient ascending을 해주고 있고 , Generator는 Loss Function을 최소화 시켜야 하므로 Gradient descending을 해주고 있습니다.

Theoretical Results

자 지금까지 GAN의 아이디어를 알아봤고 Discriminator , Generator에 대해 알아봤으며 전체적인 train 과정을 알아봤습니다.

이제 다음으로 GAN 알고리즘을 이론적으로 뒷받침해주는 근거에 대해 알아보겠습니다.

앞서 소개한 MinMax Problem에 P_{g}=P_{data} Global한 Optimum으로써 unique한 solution을 갖는다는 것을 확인할 것이고

다음으론 P_{g}=P_{data} Global Optimum으로 수렴할 수 있는지 확인할 것입니다.

일단 가장 먼저 고정된 , 임의의 G에 대해 optimal discriminator가 다음과 같다는 것을 증명하겠습니다.

optimal discriminator는 고정된 G에 대해 V(G,D)를 최대화 시키는 방향성을 가져야합니다.

• V(G,D)=E_{x\sim p_{data}(x)}[logD(x)]+E_{z\sim p_{z}(z)}[log(1-D(G(z)))]

• V(G,D)=\int\limits_{x} p_{data}(x)\times logD(x)dx+\int\limits_{z} p_{z}(z)\times log(1-D(G(z)))dz —– (1)

• V(G,D)=\int\limits_{x} p_{data}(x)\times logD(x)dx +\int\limits_{x} p_{generator}(x)\times log(1-D(x))dx —– (2)

• V(G,D)=\int\limits_{x} p_{data}(x)\times logD(x)+p_{generator}(x)\times log(1-D(x))dx

p_{data}(x)\times logD(x)+p_{generator}(x)\times log(1-D(x)) 의 최댓값은 a\times log(x)+b\times log(1-x) 의 최대값을 구하는 문제로 생각할 수 있고 간단하게 미분을 통해 x= \frac{a}{a+b} 에서 최대를 가지는 것을 확인할 수 있습니다.

이를통해 Optimal Discriminator = D^{{}\ast_{{}} }_{G}(x)=\frac{p_{data}(x)}{p_{data(x)}+p_{generator}(x)} 임을 확인할 수 있습니다.

조금 이해가 가지 않았던 것은 (1)에서 입력데이터는 분명 유한할텐데 무한한 continous random variable 의 Expectation 공식을 가져왔다는 점이고 , (2)에서 적분 변수가 바뀌는 과정이 단번에 이해가 가지는 않았습니다.

이 결과를 바탕으로 MinMax Problem을 다시 셋팅해본다면

C(G)=E_{x\sim p_{data}}[log\left( \frac{p_{data}(x)}{p_{data}(x)+p_{generator}(x)} \right)  ]+E_{x\sim p_{generator}}[log(\frac{p_{generator}(x)}{p_{data}(x)+p_{generator}(x)} )]

와 같이 변수가 G(generator) 하나 뿐인 C(G) 이렇게 표현할 수 있습니다.

그 다음으로는 C(G)의 전역해가 과연 p_{g}=p_{data} 인지 알아보겠습니다.

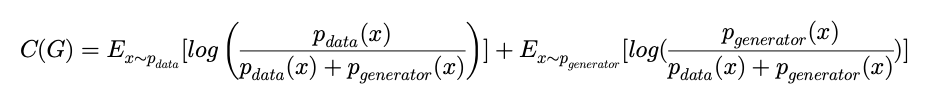
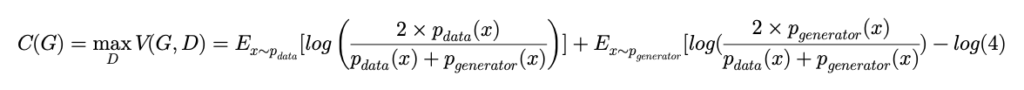
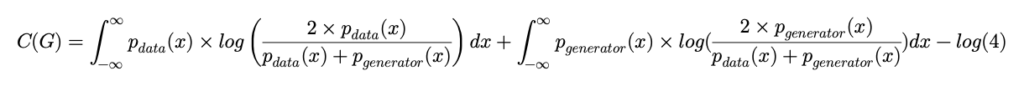
여기서 Kullbeck-Leibler divergence라는 측정값을 사용하는 데 이는 P라는 확률분포와 Q라는 확률분포가 있을 때 두 분포가 얼마나 다른지를 나타내는 값이라고 합니다. KL(P\parallel Q)=\int^{\infty }_{-\infty } p(x)\times log\frac{p(x)}{q(x)} dx

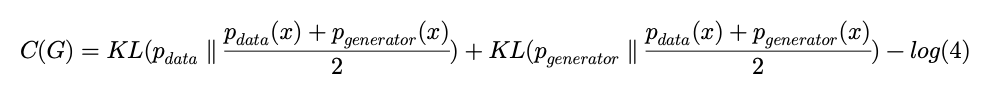
Jensen Shannon divergence 라는 개념이 등장하는데 이는 두 분포간의 차이(distance)를 나타내는 값으로 항상 양수 이며 , 비교하는 두 분포가 일치할 때만 값이 0이 나옵니다. JSD(P\parallel Q)=\frac{1}{2} KL(P\parallel M)+\frac{1}{2} KL(Q\parallel M)

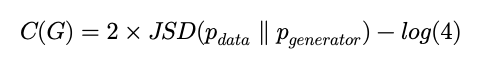
JSD가 0이 나와야 C(G)가 -log(4)의 최소값을 가지기 때문에 p_{g}=p_{data} 가 Global solution이자 유일한 solution이라는 것을 확인했습니다.

이제 마지막으로 Global Solution으로 과연 수렴을 할 수 있을지에 대해 알아보겠습니다.

사실 이부분은 제대로 이해를 못해서 가볍게 다루고 넘어가겠습니다.

여기서는 제약조건이 필요합니다. 먼저 G,D 모델이 각각 데이터의 확률 분포를 표현하거나 구별 할 수 있는 모델을 학습할 수 있을 만큼 용량이 충분해야하고 Discriminator가 고정된 G에 대해 최적값인 D*로 수렴해야 합니다.

앞의 가정이 충족 되었다면 V(G,D)=U(p_{g},D) 라 표현하고 이를 pg에 대해 편미분한 값이 Linear하게 나오므로 U가 Convex하기 때문에 수렴할 수 있다고 나와있는데… 이게 음 저는 뭔 소린지 이해를 하지 못했습니다..

Conclusion

Review가 길어진 것 같은데… GAN의 장점과 단점만 간단하게 알아보고 Review를 마치도록 하겠습니다. 장점으로는 Markov chain을 사용하지 않아도 되므로 따라서 Computation 이득이 있습니다. 단점으로는 Mod Collapse 문제 , Non-Convergence 문제 등이 있습니다.

장단점에 대해서는 또 따로 논문들을 찾아봐야 자세하게 얘기를 할 수 있을 거 같은데 이번에 GAN에 대해 알아봤으니 GAN의 후속연구들도 간간히 Review 해야겠습니다.