이번 리뷰의 주제는 제목에서도 알 수 있듯이 Multi-spectral 영상의 Structure Consistency를 향상시키는 논문입니다.
먼저 서로 다른 spectral의 카메라를 사용함으로써 얻는 이점은 자세히 말할 필요도 없으며 Multi-spectral Dataset은 많은 computer vision task에서 사용할 수 이습니다.
하지만 각각의 Spectral에서 촬영한 데이터 셋이므로, 최소 2대 이상의 카메라로 데이터 셋을 촬영하기에 실제 task에서 사용하기 위해서는 두 카메라에서 촬영된 scene이 픽셀 단위로 정합되어야만 합니다.
데이터 셋 촬영 시스템 단위에서 align을 맞추기 위해 세팅해놓을 수도 있지만, 데이터 셋 촬영 중 카메라의 큰 움직임 등으로 인하여 교합이 맞추어지지 않을 수 있겠죠.
게다가 Multi-spectral 특성 상 영상의 pixel intensity나, gradient variation이 매우 다르기 때문에, 일반적인 image align method는 사용할 수 없습니다.
그래서 해당 논문에서는 계산 효율성도 좋으며 multispectral 영상들의 intensity consistency로 향상시키는 방법론을 제안합니다.
논문에서 제안하는 방법은 structure consistency boosting(SCB)변환으로, 해당 변환 방법은 영상 본연의 엣지 구조들은 서로 다른 스펙트럼 밴드를 따라 상대적인 saliency를 보존하고 있을 것이다 라는 가정이 있습니다.
그래서 SCB 변환은 위에서 말한 영상 명도이 상대적인 saliency를 변환함으로써, multi-spectral 영상의 consistency를 향상시킵니다.
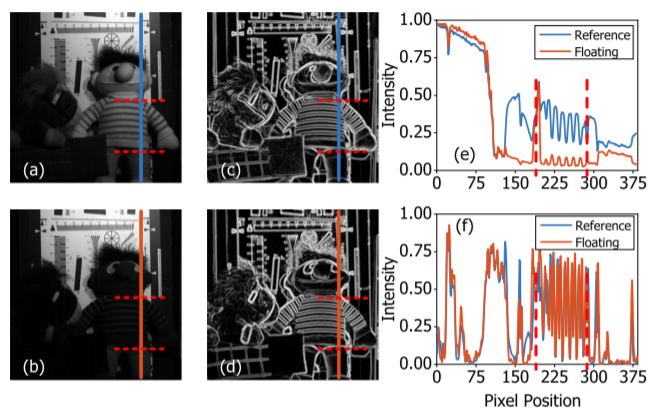
그림 1은, 동일한 장면에 대해 두개의 서로 다른 spectral band로 구성된 영상에 SCB 변환을 적용한 것입니다. 그림 1의 (e)를 보시면 빨간색 점선으로 구성된 부분은 사진 속 인형의 옷을 나타낸 부분으로 두 spectral 영상 간 명도 차이가 심한 것을 볼 수 있습니다.
하지만 그림1의 (f)에서 SCB 변환을 처리한 이후를 살펴보면 두 영상간에 intensity 분포가 몹시 일관성 있는 것을 볼 수가 있습니다.
이러한 SCB 변환을 기반으로 하여 저자는 multispectral image registration을 수행했다고 하는데, 과정은 다음과 같습니다.
- Window 안에서의 local mean intensity에 관한 픽셀 기울기의 saliency를 평가함으로써 SCB 변환을 수식화함.
- 자연적 영상들의 통계학적인 관점에서 또는 더 특별한 gradient-intensity correlation을 탐구하고, 일반적인 가우시안 함수를 통하여 이를 모델링함.
- 적은 양의 학습 데이터를 통해 파라미터들을 학습함으로써 SCB 변환을 최적화하게 계산함.
- 영상 피라미드와 gradient descent를 이용해 image registration framework를 나타냄.
SCB Transform
그림 1의 (e)를 살펴보면, 두 영상 사이에 intensity variation이 비선형적임에도 불구하고 인형 옷의 줄무니 inherent edge 구조가 상대적인 salient를 유지하고 있습니다. 여기서 inherent edge 구조는 픽셀 기울기를 참조하고 있으며, 이 픽셀 기울기의 크기는 local area 안에서 상대적으로 큰 값을 가집니다.
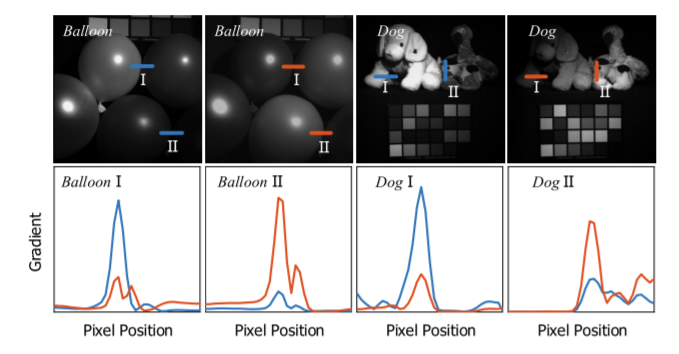
예를들어 그림 2를 살펴보면, 1행 1열의 I와 2행 1열의 I는 inherent edge 구조의 강도가 다르지만, 그들의 상대적인 saliency는 여전히 잘 유지되고 있음을 알 수 있습니다.
논문에서 제안하는 SCB 변환은 영상의 명도에서 inherent edge 구조의 상대적인 saliency를 변환하는데 목적을 두고 있으며 이는 multi-spectral image의 consistency를 향상시켜줄 수 있을 것이라고 합니다.
SCB 변환을 수식화하기 위해서, 먼저 픽셀 p와 이웃 픽셀 q에 대한 기울기를 수식(1)과 같이 계산해야만 합니다.
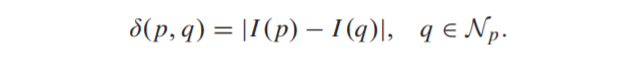
수식(1)을 보면, Multi-spectral image에서 널리 발생하는 gradient reversal 문제를 피하기 위해 절대값 연산을 취했다고 합니다. \mathcal{N}_{p} 은 윈도우를 나타내며 크기는 3 × 3, 5 × 5, 7 × 7로 설정할 수 있다고 합니다.
Inherent edge 구조는 중심 픽셀 주변에 locacl area 내에서 상대적인 salient이어야만 합니다. saliency evaluator는 수식 (2)와 같이 정의하였는데,
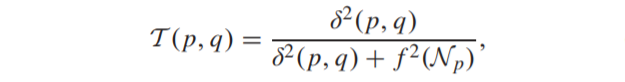
f(\dot{})는 \mathcal{N}_{p}로 부터 mean intensity와 같은 통계적인 계산을 할 수 있는 함수입니다.
f(\mathcal{N}_{p}) 는 기울기 \delta(p,q)의 상대적인 saliency의 정도를 나타냅니다.
만약 \delta(p,q)가 f(\mathcal{N}_{p})보다 매우 크게 나타난다면, \mathcal{T}(p,q)는 1에 근접하게 됩니다.
이는 edge structure(gradient)가 local area 내에서 매우 salient하다는 것을 의미합니다.
반대의 상황에서는 \mathcal{T}(p,q)가 0에 근접할 것이며 이는 saliency를 나타내는 구조가 없다는 것을 의미합니다.
저자는 SCB 변환을 모든 (p,q) 픽셀 쌍으로 통합함으로써 수식화하였는데, 이는 식(3)과 같습니다.
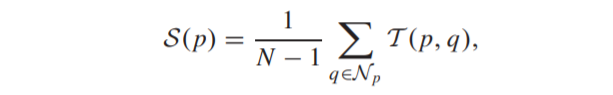
N은 이웃 윈도우의 크기를 나타냅니다. 위에 수식에 따라, f(\mathcal{N}_{p})는 자연 영상의 통계학적 prior을 조사함으로써 구할 수 있으며, 그러므로 multi-spectral 영상들 사이에서 구조적 consistency는 변환 수식(3)에 따라 향상될 수 있습니다.
Gradient-Intensity Correlation Prior
이미지 기울기의 희소성은 image denoising, deblurring 등등 다양한 영상처리 task에 널리 사용되고 있습니다. 위에서 설명한 수식(1) 역시도 희소성 특성을 잘 보존하고 있죠.
저자는 그림 4의 a와 같이 모든 픽셀 쌍으로부터 기울기 \delta(p,q)의 로그 확률을 계산하여 plot하였습니다.
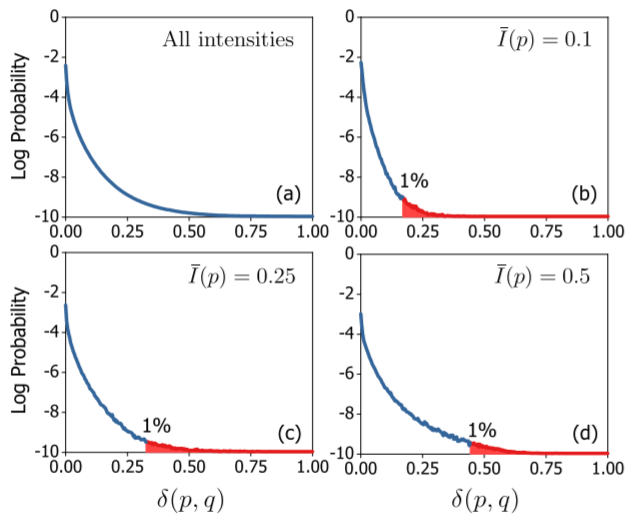
3 × 3 크기의 윈도우로 자연 영상의 기울기를 구하였습니다.
분포는 대략적으로 라플라시안이나 하이퍼 라플라시안에 가까운데, 이는 큰 기울기 값을 가지는 edge structure는 영상 내에서 매우 드물게 분포합니다.
더 나아가, local neighborhood window의 mean intensity level을 달리하여 gradient를 구함으로써 inherent edge 구조의 relative saliency를 더 상세히 조사할 수 있었다고 합니다.
그림 4의 (b), (c), (d)는 각각 mean intensity level을 0.1, 025, 0.5로 맞추어 기울기의 로그 확률 분포를 그린 것으로, 그림 4 는 2개의 사실을 보여줍니다.
먼저 첫번째는, 기울기의 희소성이 모든 intensity 뿐만 아니라 다양한 intensity level에서도 나타나는 것을 볼 수 있으며, 두번째는 가장 큰 1% 기울기에 대한 lower bound 범위가 각각에 mean intensity level에 따라 다양하게 나타나는 점입니다.
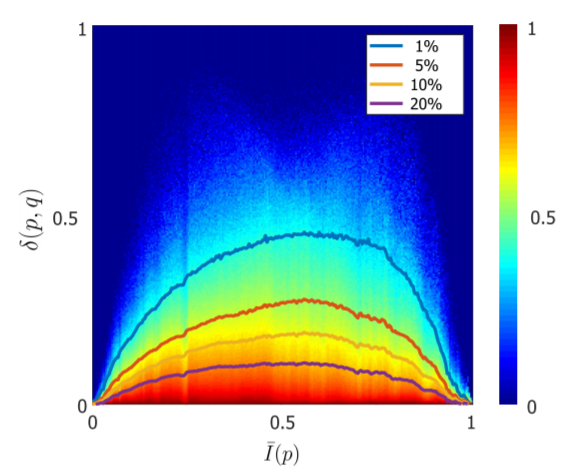
저자는 또한 기울기 \delta(p,q)와 mean intensity level \bar{I}(p) 에 대한 히스토그램을 그림 5와 같이 나타내었습니다.
해당 히스토그램은 어느 intensity level에서도 대부분의 기울기 값이 0에 근접하는 것을 보이고 있으며, 이는 기울기의 희소성(sparsity)가 모든 intensity level에서 범용적인 속성인 것을 나타낸다고 볼 수 있습니다.
내용이 너무 길어져서 뒷 내용은 다음주 리뷰에 작성하겠습니다.