Multiview Geometry(Pseudo Inverse ~ RANSAC)

오랜만에 Multi view Geometry에 대한 내용으로 리뷰를 쓰려고 합니다. 지난번까지는 Homogeneous coordinate 부터 Perspective Transformation에 대한 내용들을 다루었었고, 마지막에 Perspective Transformation을 계산하는 방법에 대해 간략히 알아보았습니다.(http://server.rcv.sejong.ac.kr:8080/2020/07/19/multiview-geometryhomogeneoushomography/ 참조)

이번 리뷰에서는 Perspective Transformation을 구하는 방법인 SVD와 RANSAC에 대해 정리하고자 합니다.

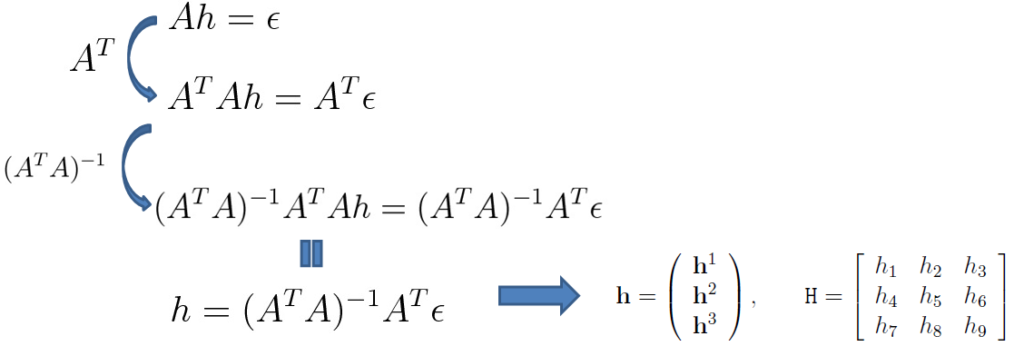
일단 이전 리뷰 마지막부분에 대해 간략히 다시 설명드리자면, 투영 변환은 위와 같이 3×3 행렬로 이루어져있습니다.

여기서 맨 마지막 원소 h_{9}는 Homogeneous coordinate 계산을 위한 행렬의 scale 값이기 때문에 항상 1이라는 고정값을 가지고 있습니다.

즉 투영 변환을 얻기 위해서는 8개의 파라미터 값만을 구하면 되는 것이고, 이를 위해 최소 4개의 대응점 쌍이 필요하다고 했었습니다.

이것은 이제 이론적인 내용이이고, 현실적으로는 데이터에 노이즈가 존재하기 때문에, 저희는 4개 이상의 대응점 쌍을 가지고 계산을 하게 됩니다. 위에 그림으로 말하자면 대응점 쌍을 나타내는 행렬 A의 row size는 4가 아닌 N이라는 것이죠.

이로인하여 구하고자 하는 파라미터의 개수 보다, 방정식의 개수가 더 많게 되는 Over determined 현상이 발생하게 되며, 이를 해결해주기 위해 위에 2, 3번째 수식과 같이 A^{T}와 (A^{T}A)^{-1}를 양변에 곱해주는 Pseudo Inverse 기법을 통하여 h를 구할 수 있었습니다.

SVD

하지만 이러한 Pseudo Inverse를 통하여 투영 행렬을 구하는 방식에는 사소한 문제가 하나 존재합니다. 바로 방정식의 결과값이 0이 되는 경우입니다.

예를 들어 만약 Ah = \epsilon 가 아닌 Ah = 0가 되는 상황이 있다고 가정해봅시다. 이 경우에도 똑같이 A^{T}와 (A^{T}A)^{-1}를 순서대로 양변에 곱해주게 되면, 우변에는 결국 0이기 때문에 결국 h = 0이라는 결과가 나오게 됩니다.

즉 투영 행렬 h를 구할 수 없게 되는데, 이러한 방식을 풀기 위해서는 Singular Value Decompositon(SVD)이라는 방식을 사용하게 됩니다.

SVD란 어떠한 m × n 크기의 행렬을 아래 그림과 같이 분해하여 나타내는 방법을 말합니다.

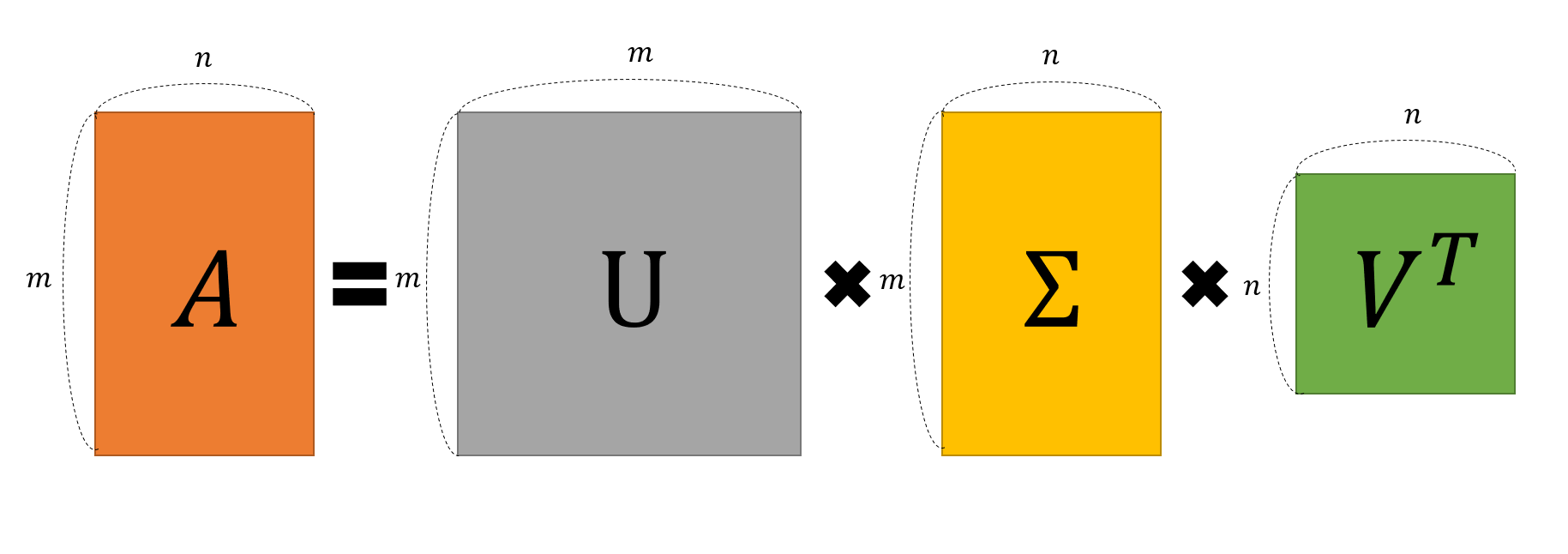
즉 m이 n보다 더 큰 행렬 A는 over determined 상황이며, 이를 m × m , m × n, n × n으로 쪼개서 나타낸다는 것이죠.

Ah = 0에서 \|Ah\| 값을 minimize하게 하는 h를 구하고자 SVD를 적용하면 다음과 같이 나타낼 수 있습니다.

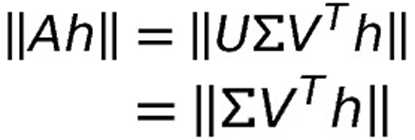
행렬 U는 orthogonal matrix로 orthogonal matrix의 특징 중 하나는 norm 값이 항상 1이기 때문에 orthogonal matrix는 어떤 행렬의 norm 값에 영향을 주지 못합니다.

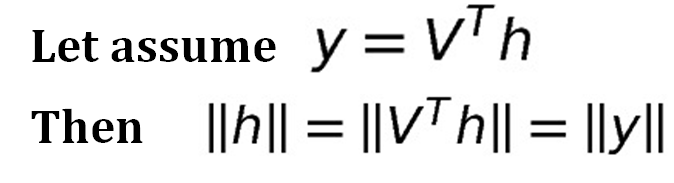
자 그리고 이제 V^{T}h를 y라고 놓았을 때, norm 값에 대해 위에 수식처럼 표현할 수 있는데, 이 역시도 V^{T}가 orthogonal matrix이기 때문입니다.

그러면 이제 우리는 기존 \|Ah\| 값을 minimize하게 하는 h를 구하는 문제에 대해서 \|Dy\| 값을 minimize하게 하는 y를 구하는 문제로 바꿔서 생각할 수 있게 됩니다.

이때 행렬 D는 diagonal matrix로 아래 예시와 같이 행렬 내 원소 값이 내림차순으로 정렬되어 있는 특징이 존재합니다.

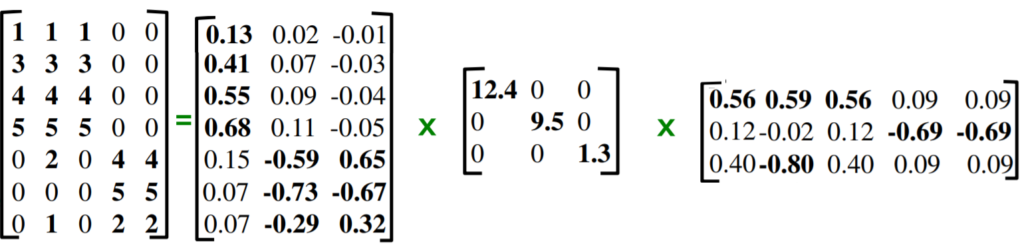
즉 \|Dy\| 값을 minimize 하게 만드는 y를 구하기 위해서는 D의 제일 마지막 column만을 가져오고 나머지는 다 0으로 만들게 하면 되기 때문에, y는 맨 마지막 원소만 1을 가지는 꼴인 [0 0 0 0 .... 1]^{T}이 되면 됩니다.

여기서 y = V^{T}h 이기 때문에, h = Vy 가 되며, 이 때 y는 [0 0 0 0 .... 1]^{T} 이므로 최종적으로 h는 V의 마지막 column vector를 가지게 됩니다.

RANSAC

SVD를 통한 투영 변환 행렬 구하는 방법에 대해 알아보았으니 이제는 가장 흔하게 사용되는 RANSAC에 대해서 알아봅시다.

RANSAC이란 RANDOM SAMPLING CONSENSUS의 약자로, 우리가 구하고자하는 모델을 구축하는데 있어 필요한 최소한의 데이터 개수를 랜덤하게 샘플링하여 모델 파라미터를 추정하는 것입니다.

전체적인 파이프라인은 아래와 같습니다.

1. 추정할 모델에 필요한 최소한의 데이터 개수만큼 샘플링하여 임의의 모델을 추정한다.
2. 추정된 모델과 전체 데이터들 간에 거리를 비교한 후 일정 임계치 값 이내에 위치하는 inlier들의 개수를 구한다.
3. 1~2번 과정을 반복하여 가장 많은 inlier 개수를 가지는 모델의 파라미터 값을 RANSAC의 최종적인 결과값으로 사용한다.
4. + optional한 단계로, 3번에서 구한 모델의 inlier들을 대상으로 하여 다시 Pseudo Inverse를 통한 모델의 파라미터 값을 추정.

차근차근 설명을 드리자면 먼저 1번에 경우 만약 우리가 구하고 싶은 모델이 직선이면 전체 데이터 중 랜덤하게 2개의 데이터를 샘플링하면 되는 것이고, 만약 포물선을 추정하고 싶으면 랜덤하게 3개의 데이터를 샘플링하는 것입니다.투영 변환의 경우에는 4개의 점을 샘플링하면 되겠죠?

그렇게 샘플링한 데이터를 토대로 어떠한 모델을 만들게 되면 이제 전체 데이터에 대하여 inlier 개수를 수집하게 됩니다.

아무래도 랜덤하게 데이터를 샘플링하여 모델을 수행하였기 때문에, 운이 정말 좋지 않는 이상은 inlier 개수가 적은 모델들이 추정될 확률이 높을 것입니다.

하지만 위의 과정을 반복해서 진행하다 보면 inlier 개수가 제일 많은 모델이 추정될 것이며, 이는 outlier까지 모두 포함하여 한번에 계산해버리는 Pseudo Inverse나 SVD보다 훨씬 정교한 결과를 얻게 됩니다.

즉 RANSAC은 outlier에 강인함을 보이며 이러한 RANSAC을 사용하기 위해서는 아무래도 랜덤하게 샘플링하는 것이므로 데이터의 개수가 많아야 좋다고 합니다.

아 그리고 파이프라인 중 4번째 단계에 대해 설명드리자면, RANSAC을 통해 최종적으로 구한 모델은 inlier의 개수가 제일 많은 모델이기 때문에, 이 모델의 inlier 데이터들은 기존에 전체 데이터와 비교하면 제법 깨끗한 데이터라고 가정할 수 있습니다.(마치 outlier가 한번 필터링 된 것으로 보시면 될 것 같습니다.)

그래서 이러한 inlier들을 가지고 기존 outlier에 취약한 SVD나 Pseudo Inverse로 다시 한번 모델의 파라미터를 구하게 되는 것이 4번째 단계를 의미합니다. 그래서 optional한 step이라고 하는 것이구요.

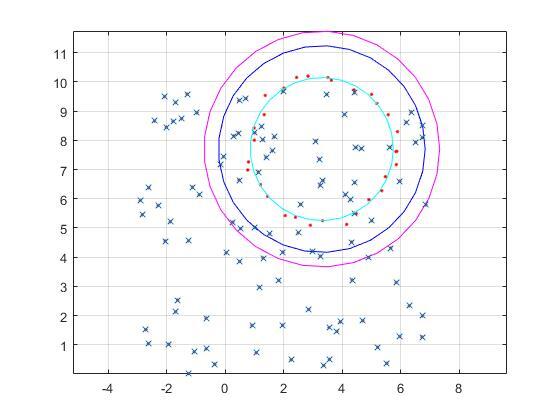
위에 그림은 matlab 코드를 통해 Pseudo Inverse, SVD, RANSAC의 결과값을 나타낸 것입니다. 빨간색 점은 우리가 추정해야할 실제 데이터를 의미하며, x 모양의 데이터는 outlier를 나타냅니다.

마젠타 색상의 원이 Pseudo Inverse로 추정한 원이며, 파란색 원은 SVD, 민트색 원이 RANSAC을 이용한 결과값입니다.

보시면은 Pseudo Inverse와 SVD는 outlier에 민감하여 정확한 추정이 안되는 반면, RANSAC은 비교적 정확하게 빨간색 점들을 근사하는 모습입니다.

물론 RANSAC 역시 outlier의 개수가 많아지면 많아질수록 제대로 된 추정이 불가능하며, 동일한 outlier의 개수를 가진다고 하더라도, 추정하고자하는 모델이 더 복잡해지면 정확한 모델을 구하기 어려워집니다.(즉 모델에 사용되는 random sample의 개수가 커질수록 outlier에 취약해짐.)

위에 결과에 사용된 코드를 마지막으로 리뷰를 마치겠습니다.

% Generating points on a circle
 clear; clc;
 th = linspace(0,2*pi,30)';
 r = 2.5;      % radius of circle
 ox = 3.3;     % center of circle in x-axis
 oy = 7.7;     % center of circle in y-axis
 scale = 0.1; % noise level
 x = rcos(th) + ox + randn(size(th))scale;
 y = rsin(th) + oy + randn(size(th))scale;
 %outlier
 outNum = 100;
 Xo = (rand(outNum,1))10- 3; Yo = (rand(outNum,1))10;
 x = [x; Xo];
 y = [y; Yo];
 %-----------------------LSM-------------------------------
 X1 = [x, y, ones(size(x))];
 Y1 = [x.^2+y.^2];
 p1 = inv(X1'X1)X1'*Y1;
 r1 = sqrt(p1(3) + (p1(1)/2)^2 + (p1(2)/2)^2);
 x1 = r1cos(th) + ox; y1 = r1sin(th) + oy;

 %-----------------------SVD-------------------------------
 X2 = [x.^2 + y.^2, -x, -y, ones(size(x))];
 [U D V] = svd(X2);
 p2 = V(:,end);
 p2 = p2/p2(1);
 r2 = sqrt((p2(2)/2)^2+(p2(3)/2)^2 -p2(4));
 x2 = r2cos(th) + ox; y2 = r2sin(th) + oy;

 %----------------------RANSAC----------------------------------
 p = 0.99;
 e = outNum/length(x);
 s = 3;
 N = log(1-p) / log(1-(1-e)^s);
 thresh = 0.1;
 max = 0;
 Y3 = [x.^2+y.^2];
 for i=1:ceil(N)
     id = randperm(length(x), s);
     X3 = [x(id), y(id), ones(s,1)];
     p3 = inv(X3'X3)X3'Y3(id);     err = abs([x, y, ones(size(x))]p3 - Y3);
     cnt = sum(err<thresh);
     if max < cnt
         max = cnt;
         pmax = p3;
     end
 end
 err = abs([x, y, ones(size(x))]pmax - Y3); id = find(errX3)X3'Y3(id);
 r3 = sqrt(p3(3) + (p3(1)/2)^2 + (p3(2)/2)^2);
 x3 = r3cos(th) + ox; y3 = r3sin(th) + oy;
 %------------------------------------------------------------
 figure; plot(x, y, 'r.'); axis equal; grid on; hold on;
 plot(x1, y1, '-m'); %Pseudo Inverse result
  plot(x2, y2, '-b'); %SVD result
 plot(Xo, Yo, 'x'); %outlier포함
 plot(x3, y3, 'c'); %RANSAC result
 hold off;