해당 논문은 ECCV2016에 나왔던 Colorization의 초기 논문 중 하나입니다. 워낙 꽤 오래된 논문이긴 하지만, Colorization에 대해 매우 기초적인 논문이기도 하고 인용수도 현재 기준 1296회나 될 정도로 많기에 리뷰해보고자 합니다.
Introduction
일단 Colorization은 지난 번 리뷰에서도 말씀드렸다시피, gray scale image를 color image로 즉1채널 이미지를 입력으로 하여, 2개의 채널을 추가로 예측하는 작업을 말합니다.
보통 Colorization의 일반적인 방식? 및 목적은 GT 영상과 동일한 색상의 Color로 모델이 예측하고자 하지만, 해당 논문의 목적은 특이하게도 GT와 색상이 일치할 필요는 없이 사람의 눈으로 볼 때 자연스럽게만 출력되게끔 하는 것입니다.
예를 들어 빨간 사과를 GT로 주었다면 학습된 모델이 반드시 빨간색을 낼 필요는 없이, 초록색 사과를 출력해도 된다는 것이죠.(물론 주황색 사과는 틀린 결과값이 됩니다.)

그림1또 다른 예시로는 위에 사진을 통해 확인하실 수 있습니다. 좌측 영상은 해당 논문을 통해 Colorization한 것이고, 우측 영상이 실제 GT 영상이죠.
보시면 예측값이 GT값과는 전혀 반대의 색상으로 Colorization을 하였지만, 사람 눈으로 봤을 땐 어색하게 느껴지지 않기 때문에, 성공적으로 Colorization 됐다고 보는 것입니다.
입력 영상은 당연히 gray scale image를 사용하며, predict 하는 값은 a,b 값을 예측합니다. 여기서 a,b 값은 무엇일까요?
Lab는 색상을 나타내는 방식 중에 또 한가지입니다. 다른 방식으로는 우리가 흔히 아는 RGB와 HSV등이 존재하죠. Lab에 대해서 간략하게 설명드리면 아래와 같습니다.
- L – Luminosity(명도)
- a – red와 green의 보색축
- b – yellow와 blue의 보색축
L은 입력 영상으로 사용되는 gray scale image의 명도값과 동일합니다. 그래서 우리는 L값을 입력으로 하여 a와 b값을 predict 하면 되는 것이죠.
a와 b에 대해서 조금 더 자세히 설명드리면, a의 값이 -이면 녹색에 가까우며, +값으로 갈 수록 적색에 해당됩니다. b도 마찬가지로 -값일 때는 청색 영역에 속하다가, 점점 +로 갈수록 황색 영역으로 바뀌게됩니다.
아무튼 이러한 Lab 값을 예측하다보니, Colorization만의 매우 특별한 장점이 존재하는데, 이는 바로 데이터 셋의 제약이 다른 vision task에 비해 매우 적다는 점입니다.
예를 들어 Optical Flow와 같은 vision task는 GT 값을 구하는데 매우 큰 어려움이 있어 데이터셋 자체가 매우 작은 반면, Colorization은 Color 값만 잘 있으면 언제든지 학습 데이터 셋으로 사용할 수 있는 것이죠. 해당 논문에서는 ImageNet을 통해 학습 및 테스트 한 것 같습니다.
Architecture
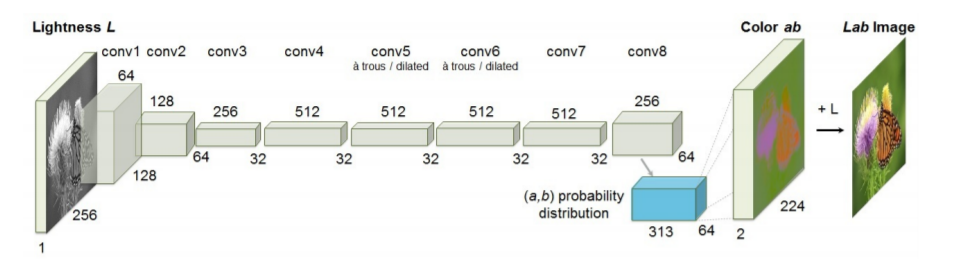
위 그림은 해당 논문에서 제안하는 방법론의 Architecture로 총 8개의 블록(그림상 하얀색)으로 구성되어 있습니다. 각 블록은 2~3개의 컨볼루션 레이어로 구성되어 있으며 ReLU와 Batch Normalization도 사용됩니다.
또한 pooling 대신에 Stride 값을 크게하여 영상의 사이즈를 감소시켰습니다. 입력 영상의 사이즈는 256×256인 반면, output size는 224×224 인데 이 출력값은 나중에 입력영상과 동일한 사이즈로 resize 된다고 합니다.
Objective Function
해당 논문의 목적은 위에서 설명드렸다시피 L 채널의 영상을 입력으로 하여 이와 관련된 컬러 채널 a,b를 예측하는 것입니다.
여기서 Lab 표기를 사용하는 이유는, 해당 공간 모델의 perceptual distance를 예측된 색상과 GT 색상 사이의 euclidean loss(L2)로 표현할 수 있기 때문입니다.
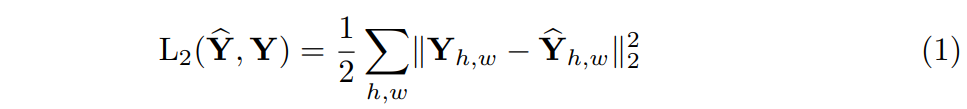
Euclidean Loss 수식
하지만 이 loss 함수는 Colorization의 근본적인 애매호호함 문제에는 강인하지 못합니다. 예를 들어 만약 어떤 물체가 아래 그림에 좌측과 같이 서로 반대되는 a,b set을 지니고 있다면, euclidean loss에서 나타나는 최적의 해결책은 이 a,b set에 대한 평균 값을 취하는 것입니다.
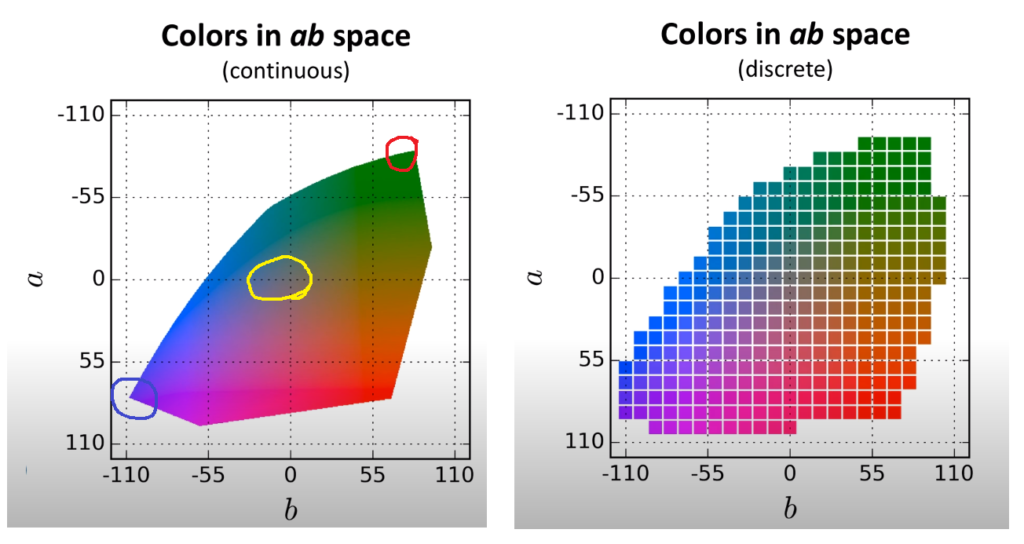
그림2 ab space를 continuous하게 한 것(좌측)과 해당 논문에서 제안하는 discrete 그래프(우측) 하지만 색상 관점에서, 이러한 평균 값을 취하는 것은 색상을 보다 회색 빛으로 나게끔 하는, 즉 desaturated한 결과값을 나타내게 됩니다.
Desaturation이란 쉽게 말하면 영상을 표현하는 색상이 흰색 또는 검정색의 영향이 더 강한 것을 의미하며 반대로 Saturation에 경우에는 흰색 또는 검정색의 영향이 작으므로 채도 값이 더 뚜렷한 것을 알 수 있습니다.

그림3 원본 영상(중앙)에 대한 Desaturation(좌측)과 Saturation(우측) 영상.Destaurated image에 경우 영상의 색상이 회색에 가까우며 이러한 결과는 Colorization에서 바람직한 결과값이 아니다. 다시 본론으로 돌아와서, 이 논문에서는 이러한 euclidean loss의 문제를 해결하기 위하여 그림2 우측과 같이 a,b 출력 공간을 10 간격으로 양자화하였습니다. 이렇게 양자화를 하여 총 Q=313개의 색상 값으로 구분한 것이죠.
그 다음은 이제 입력 X에 대해서 변경가능한 색상 분포값으로 매핑하게 되는 G함수를 학습하게 되는 것입니다.(\hat{Z} = G(X)) 이 때 Z의 채널은 H×W×Q를 가지게 된답니다.
그럼 이렇게 구한 \hat{Z}와 GT를 비교하기 위해서 GT 영상 Y에 대한 분포 벡터 Z도 계산을 해줘야하는데, 이는 soft-encoding 기법을 사용한 함수(H)를 정의하여 Z = H^{-1}_{gt}(Y)를 통해 계산할 수 있습니다.
그리고 나서는 아래 수식과 같은 multinomial cross entropy loss를 적용하였습니다.
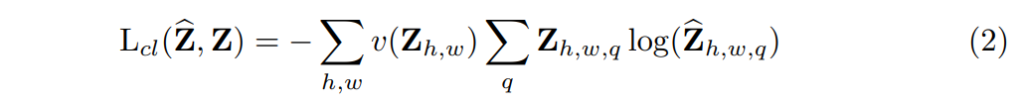
v()는 가중치 텀으로 색상 클래스의 희소성에 기반하여 loss 값을 재조정하는 역할입니다. 마지막으로 \hat{Y} = H(\hat{Z})을 통해 확률분포인 \hat{Z}을 컬러 값 \hat{Y}으로 매핑합니다.
위에 내용을 간략히 요약하자면 기존에 euclidean distance를 통한 loss 기법은 최적화된 방향으로 나아가고자 단순히 a,b를 평균하는 문제가 발생했기에, 이를 해결하고자 a,b를 크기 10의 간격으로 나누어 양자화하였고, Cross Entropy loss를 이용하여 분류 문제로 풀고자 한 것 입니다.
Class rebalancing
자연 영상에 대한 a,b 값의 분포는 low ab value에 강하게 편향되어 있습니다. 그 이유는 구름이나, 포장도로, 벽 같은 배경이 이러한 low value값을 가지고 있기 때문입니다. 아래 그림은 이미지 넷에 있는 1.3M 개의 학습 영상을 모아서 a,b space에 대한 픽셀들의 경험적 분포함수를 나타낸 것입니다.
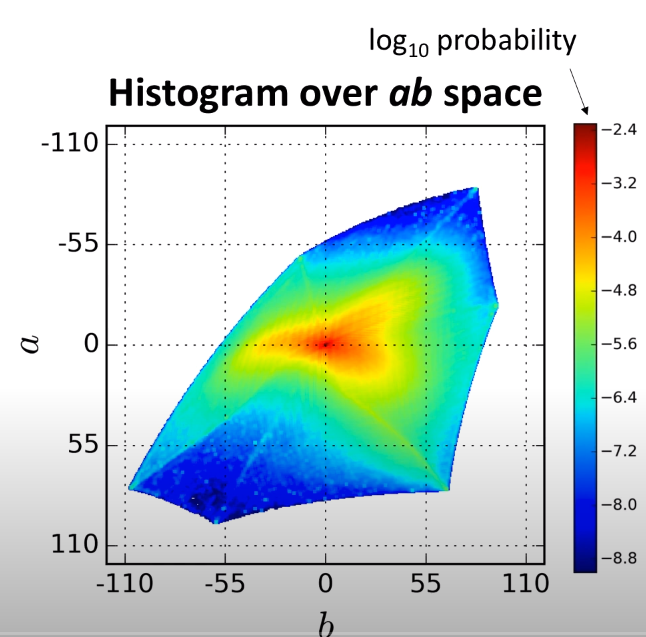
그림4보시면 많은 픽셀들이 low a,b value(중앙부분) 즉, desaturated value 값에 분포되어 있는 것을 확인하실 수 있습니다. 기존에는 이러한 상황을 고려하지 않은 채, 단순히 loss function이 desaturated a,b value들에 대해 지배당하고 있었던 것이죠.
이러한 class-imbalance 문제를 해결하고자 픽셀 컬러의 희소성을 베이스로 하여 각 픽셀의 loss를 reweighting해줍니다. 이것은 학습 공간을 resampling하는 전통적인 방법과 동일하다고 합니다.
각 픽셀은 각 픽셀에 가장 가까운 a,b bin를 베이스로 한 w 값을 통하여 가중치를 주게 됩니다.
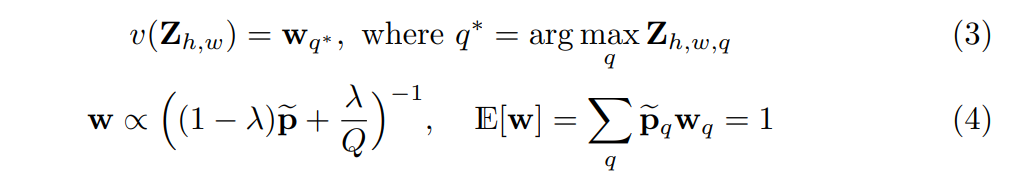
보다 부드러운 경험적 분포를 구하기 위해, 먼저 이미지넷의 학습 데이터 전체를 a,b space로 양자화하여 경험적 확률들을 추정한 후, 가우시안 커널을 통해 스무딩하였습니다. 그리고 나서 weight [0, 1]을 가지는 uniform distribution을 섞은 후 정규화하여 가중치의 기대치가 1이 되게끔 하였습니다.
Class Probabilities to Point Estimates
마지막으로 예측한 분포벡터 \hat{Z}을 a,b space인 \hat{Y}으로 mapping하는 함수인 H에 대해서 알아봅시다.
일단 크게 2가지 방법이 존재하는데, 먼저 첫번째 방법은 모든 픽셀에 대해서 예측된 분포 값의 mode를 가져오는 방법이 있고, 나머지 방법은 예측된 분포 값의 평균 값을 취하는 방법이 존재합니다.
mode란 쉽게 말해 해당 분포 내에서 가장 많이 출현한 값으로 바꿔서 말하면 확률값이 제일 큰 값을 의미합니다. 즉 0~312길이의 Z 벡터에 대해서 제일 큰 확률값을 가지는 bin(class)를 argmax해서 가져온다는 것 같습니다.
이를 통해서 색상을 맵핑하게 되면, 영상의 색상은 매우 선명해지나, 부분적으로 일관성 없는 색이 입혀지기도 합니다.(아래 그림 중 제일 오른쪽 Column 참조)

그림5반대로 분포의 평균을 통해 색상을 맵핑하게 되면 부분적으로 튀는 부분 없이 일관성을 보이기는 하지만, 색상의 결과값이 전체적으로 desaturated 한 것을 보실 수 있습니다.
이러한 결과가 나오는 이유는 뭐 당연히 분류값에 평균을 취하는 것이 위에서 설명했던 기존 regression 관점에서 Euclidean loss를 통한 최적화 기법에서의 이슈와 동일한 것이죠.
위와 같은 mode와 평균 각각에 문제를 보완하고자 소프트맥스 분포의 Temperature T를 재조정하여 보간한 후, 해당 결과값에 평균을 취했다고 합니다. 음… 이 부분에 대하여 논문에서는 annealing technique에 영감을 얻어 분포의 annealed-mean 연산을 진행하였다는데 내용이 너무 생소하더군요. 이 부분은 추후에 따로 공부하여 내용을 보충하고자 합니다.
annealing technique이란 한글로 번역하면 담금질 기법을 의미합니다. 담금질은 아시다시피 철과 같은 광물을 녹을 때까지 가열시킨 후 천천히 식힘으로써 더욱 단단하게 만드는 과정을 말합니다.
이것을 과학적인 측면에서 보면, 광물을 구성하는 원자는 안정한 상태를 유지하고 있는데, 이때 열을 가함으로써 원자가 불안정하게 됩니다.
그리고 다시 식어가는 과정을 통해 원자가 안정해지는데, 이때 기존 열을 가하기 전보다 더 안정해진 상태(에너지가 극소가 되는 지점에 도달)가 될 수 있다고 합니다. 이때 광물을 급하게 식히는 것보다, 서서히 식힐 수록 원자가 기존보다 더 안정해질 확률이 높다고 합니다.
바꿔서 말하면 인공지능에서 기본적으로 배우는 Optimization(최적화)과 매우 유사하다고 볼 수 있겠죠? learning rate를 너무 크게 하면 최적화될 가능성이 줄어들고, 반대로 learning rate를 너무 크게 하면, 최적화는 잘 되겠지만 시간이 오래걸리는 것처럼, 담금질도 너무 급하게 식히면 원자가 안정해질 확률이 줄어드는 반면, 너무 천천히 식히면 원자는 매우 안정해지겠지만 시간이 오래 걸릴 것입니다.
즉 담금질 기법이란, 실제 담금질의 원리에 영감을 받은 것으로, 어떠한 문제의 가장 최적화된 해를 효율적으로(최소한의 경우의 수로) 찾아가는 통계학적 기법을 의미합니다.
물론 담금질 기법이 최적화 기법이랑 완전히 똑같은 것은 아닙니다. 최적화 기법은 cost함수를 미분하여 현재 값에 빼는 방식으로 값을 갱신해 나아갑니다.
반면 담금질 기법은 단순히 현재 값과 다음 값을 비교했을 때 현재 값이 더 크다면 다음 값으로 현재값을 갱신하는 것입니다. 즉 제일 작은 값을 찾게끔 나아가는 것이죠.
이떄 초기 온도 T값은 매우 크며, T는 천천히 줄어들기 때문에 담금질 기법 초기 시작 값이 local minima에 빠질 확률은 매우 적습니다.(T가 크다는 것은 learning rate가 크다는 것과 유사하다고 보시면 될 것 같습니다.)
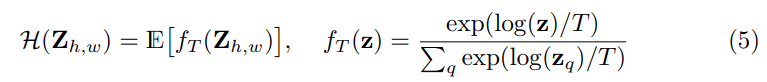
아무튼간에 논문에서는 이러한 담금질 기법에 영감을 받아 위의 수식과 같이 적용시켰습니다. 초기 T값은 1이고 T값은 서서히 줄어들면서 최적화된 값을 찾아 나섭니다.
T값이 1일 경우에는 분포의 평균값을 사용하게 되는 것을 의미하며, T가 줄어들수록 분포가 점점 뾰족해지다가 T가 0이되면 분포도 one-hot encoding이 되어 분포의 mode를 사용하는 효과를 볼 수 있습니다.
논문에서 가장 좋다고 말하는 T 값은 0.38이구요, 0.38일때의 결과값은 그림 5의 middle image를 통하여 확인하실 수 있습니다.
Experiments
먼저 정성적인 결과에 대해 다른 방법론들과 비교해봅시다.

그림6일단 제일 좌측에 Column은 input을, 제일 우측 Column은 우측을 나타냅니다. Regression은 위에서 설명드렸다시피, 유클리디안 거리를 통해 평균으로 loss를 계산하다보니, 결과 영상들이 대부분 회색 빛을 도는, desaturated한 것을 보실 수 있습니다.
또한 3번째 Column인 Classification에 경우에는, 위에서 설명한 Class-imbalance(영상들이 대부분 low a,b value인 desaturated value를 지님)를 해결하지 않았을 경우의 결과값을 나타냅니다.
이 역시 결과 영상이 선명하지 않은데, 이러한 imbalance를 reweighting을 통해 해결한 것이 바로 해당 논문에 최종 결과인 4번째 column image 입니다.
영상의 비교적 깨끗한 것을 볼 수 있으며 GT 영상과는 전혀 다른 색을 가지는 경우도 있지만 사람의 눈으로 봤을 땐 전혀 어색하지 않은 것을 정성적으로 확인할 수 있습니다.
물론 위에 정성적 이미지들은 성공case만을 보여준 것이고, 실패한 case들은 아래 사진을 통해 확인하실 수 있습니다.

그림7아래는 정량적인 결과 테이블입니다. 먼저 평가 방식에 대해서 잠깐 살펴봅시다.
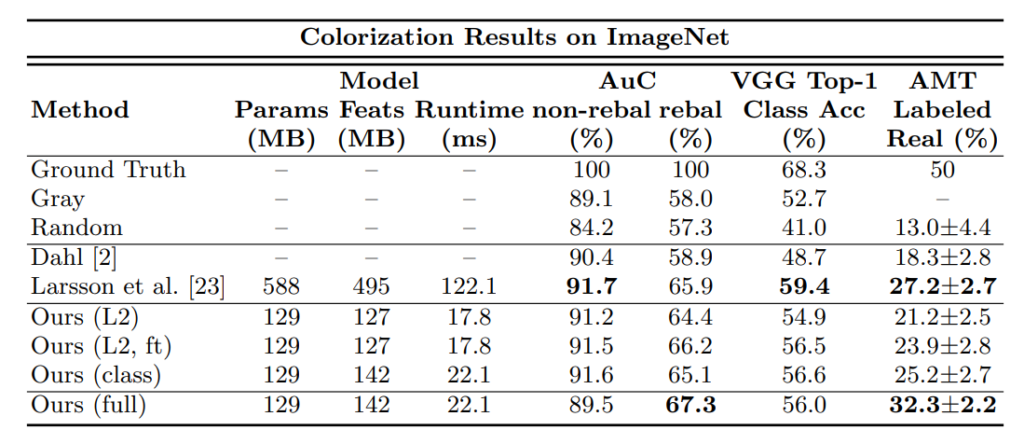
평가 지표는 크게 Raw accuracy(AuC), Semantic interpretability(VGG Top-1), AMT로 적혀있습니다.
먼저 RAW accuracy는 a,b color space에 대한 GT 값의 L2 distance를 임계치로 가져서 예측된 픽셀 컬러의 퍼센테이지를 계산한 것입니다.
그래서 L2 loss를 사용하는 Larsson 방법론이 정확도 면에서는 더 좋은 성능을 보이고 있지만, 이 metric은 desaturated pixel에 지배적이기 때문에, 대부분의 픽셀 값을 회색으로 예측해도 위에 방식으로는 좋은 성능을 낸다고 볼 수 있는 것입니다.
반면 논문에서 제안하는 방식은 gt와 동일한 컬러로 예측하는 것이 아니라 사람의 눈으로 봤을 때 그럴 듯하게 보이게끔 학습하고자 했으므로 Auc 값이 다른 방법론에 비해 낮을 수는 있지만, 정성적으로 확인했을 때는 색상이 뚜렷하고 회색을 나타내는 픽셀이 적은 것을 확인할 수 있습니다.
Semantic interpretability 평가 메트릭은 요약하자면, colorization으로 만든 영상이 실제 영상과 매우 비슷하게 잘 만들어졌다면, 이전에 잘 작동하는 분류기에 인풋으로 넣었을 때 분류기가 잘 분류하지 않을까?가 컨셉입니다.
논문에서는 이미지 넷 데이터 셋(real image)으로 학습한 VGG network에 colorization 기법을 통해 만든 fake image를 인풋으로 주었고, 이때 분류기가 잘 작동하는지를 평가하였습니다.
결과표를 보시면 컬러 영상으로 학습한 VGG를 real color image로 평가하였을 때 68% 성능을 보였고, gray image로 평가할 때는 52%정도의 성능을 보였습니다. 이를 해당 방법론을 통해 colorization하여 평가하였을 경우 기존 52%에서 4% 오른 56%에 성능을 보였습니다.(물론 다른 방법론인 Larsson et al 방법론이 59%의 성능을 낸 것에 비하면 밀리긴 합니다. )
마지막으로는 이 논문의 핵심인 Perceptual realism metric입니다. 해당 방식은 사람한테 real image와 colorization을 통해 만든 fake image를 보여준 후, 어느 이미지가 컴퓨터를 통해 만든 가짜 영상인 것 같은지를 사람에게 선택하도록 하는 것입니다. 쉽게 말해 Colorization 용 Turing Test 인셈이죠.
각각의 실험 섹션에서 총 10번에 시도를 진행하였으며, 총 40쌍에 영상으로 테스트를 진행하였습니다. 또한 40쌍에 영상을 시험보는 동안 참가자들은 이전에 풀었던 문제가 정답인지 아닌지에 대한 피드백을 받지 못했다고 합니다.
위의 메트릭을 통한 결과값을 보면 해당 방법론이 다른 방법론들에 비해 제일 높은 성능을 보이는 것을 확인하실 수 있습니다. 즉 이 논문의 처음 목적인 gt와 동일한 색을 예측하는게 아닌 사람의 눈으로 볼 때 그럴듯한 색상으로 예측하자는 목적을 잘 이룬 것을 볼 수 있습니다.
심지어 어떤 참가자들에 대해서는 문제 40쌍 중에서 real 영상보다 해당 방법론으로 만든 가짜 영상이 진짜 같다고 응답한 비율이 50%를 넘긴 참가자들도 종종 존재한다고 합니다.
테스트 참가자들이 자주 헷갈렸던 영상과 헷갈리지 않았던 영상을 마지막으로 확인하시고 리뷰를 마치도록 하겠습니다.

그림8
항상 좋은 글 감사합니다. 원초적인 질문이 있습니다. 최근 리뷰에서 Optical flow, colorization, latex등을 다루셨는데 신정민 연구원님의 주된 관심사는 어떤부분에 있나요? 예를들어 object detection, image retrieval 등등… 아직 CV쪽에 많은 분야를 몰라서 그런지 항상 다루시는 주제가 생소하다는 느낌이 많이 듭니다. 어떤 연구를 하기위해서 Optical flow, colorization등을 공부하고 계신가요?
음 아무래도 관심사가 뚜렷하게 정해지지 않았다보니, 다양한 분야에 대해서 논문을 찾아보고 읽게 되는 것 같습니다.
Optical flow의 경우에는 어떠한 연구를 목표로 하고자 보았던 것은 아니었고, 김형준 연구원님이 최근에 보는 논문 중 GAN이라는 내용이 많이 나와 이번 리뷰를 했던 것처럼, 저도 Optical Flow가 간간히 나오다보니 해당 분야에 대해 알아보고자 공부했던 것 같습니다.
또한 Colorization의 경우는 계기가 진행하는 과제와 연관이 있어 공부하게 되었는데, 결과적으로는 두 분야 모두 보다보니 흥미롭기도 하고 재밌어서 리뷰를 자주 쓴 것 같습니다.
loss가 존재한다면 어떤 network의 구조가 있는 듯해 보이는데 혹시 network의 그림이 논문에 첨부되어 있을까요? 아니면 매핑함수로 pixel의 intensity를 매핑해주는 것일까요?
음 좋은 질문 감사합니다.
논문에서 네트워크 구조보다는 objective function을 깊이있게 다루다보니, 제가 network 그림 넣는 것을 깜빡하였네요 허허.
새로 추가하였습니다.
감사합니다.