이번 X-review에서는 Entropy, cross-entropy, KL-divergence에 대해서 심도있게 다루어 보겠습니다. 이번에 X-review에서 해당 내용을 다루게 된 이유는 KL-divergence loss를 공부하던 중 entropy, cross-entropy를 자연스럽게 공부하게 되어 같이 다루게 되었습니다. 해당 내용은 https://www.youtube.com/watch?v=Dc0PQlNQhGY 를 보고 참고했습니다. 해당 내용을 이해하고 좀 더 알기 쉽게 정리하려고 최대한 노력해봤습니다. 만약 이해가 안 가시면 해당 동영상을 한번 보시는 것이 도움이 될겁니다.
Entropy, cross-entropy, KL-divergence에 대하여 자세하게 학습하기 전에는 거리를 나타내는 한 개의 metric정도로 이해를 하고 있었습니다. 그러나 좀더 심도 있게 공부해본 내용에 대해서 리뷰 해보고자 합니다.

본격적으로 시작하기에 앞서 해당 질문에 답을 하실 수 있으신가요? 만약 그렇다면, 본 리뷰를 읽을 필요가 없습니다. 왜 엔트로피식에는 –가 붙는지, log함수를 왜 사용했는지 등등 이해 위주의 세부적인 내용을 다루어 보겠습니다.
Information theory에서 정보량이 무엇일까요? 이는 예시를 통해 이해하기 쉽습니다. 뻔하지 않은 이야기는 정보량이 크고, 뻔한 이야기는 정보량이 작습니다. 아래에서 예시로 설명해드리겠습니다.
ex) 해가 동쪽에서 떴대. (정보량 낮음)
해가 서쪽에서 떴대. (정보량 높음)
그렇다면 확률적인 관점에서는 어떨까요? 아시다시피 해가 서쪽에서 뜰 확률은 거의 없습니다. 0%에 수렴한다고 볼 수가 있겠는데요. 반대로 해가 동쪽에서 뜰 확률은 거의 100%에 수렴합니다. 이제 확률이 정보량과 어떤 관계를 가지고 있나 알아보기 위해 아래에 정리해보겠습니다.
- . (정보량 높음, 확률 낮음)
- . (정보량 낮음, 확률 높음)
용어를 알아야 이해가 쉬우므로 당연한 소리를 길게 했습니다. 여기까지 잘 따라오셨으면, 정보량과 확률이 어떤 의미인지 이해가 가셨을 겁니다.
그렇다면, 정보량과 확률사이의 관계는 어떻게 될까요? 예시를 보면 쉽게 알 수 있듯이, 반비례 관계입니다. 반비례 관계중에서도 monotonic한 관계입니다. monotonic이란 단조라고도 하며, 해당 예시에선 오로직 감소만 하는 것을 의미합니다. 즉, 중간에 증가 없이 계속 감소만 하는 것을 의미합니다. 여기까지 글로써 정리를 해봤습니다. 이제 이를 수식으로 나타내보겠습니다.

X는 확률변수이며, 독립변수입니다. 독립변수에 대해서는 아래에서 언급하겠습니다. h는 정보량을 나타내는 함수입니다. p는 확률을 나타내는 함수입니다. 위에서 다루었던 내용을 수식으로 나타낸 것 뿐입니다.

X가 독립변수라고 했습니다. 다들 아실거라고 생각하지만, 혹시나 해서 참고자료로 가지고 왔습니다. 확률적인 관점에서 독립이란 서로 영향을 주지 않는 경우를 의미합니다. 고등수학에서 사건이 독립일 때 확률 계산하는 법을 배웠습니다.

위에 수식을 보시면 알 수 있듯, 사건이 독립일 때 동시에 일어날 확률은 각 확률의 곱으로 나타냅니다. 이제 이 내용을 위에서 배운 정보량h와 확률p에 적용 해봅시다.
위에 내용에서 해가 동쪽에서 뜬 정보와 서울에 비가왔다는 정보는 서로 독립입니다. 이렇게 서로 독립인 정보가 여러가지가 들어왔을 때 이를 h, p, 확률변수로 나타내는 법을 알아봅시다.

확률변수 X, Y는 서로 독립인 확률변수입니다. h는 정보량을 나타내는 함수이고 p는 확률을 나타내는 함수입니다. 해당 내용에 대한 설명은 위에서 했습니다. X와 Y가 동시에 일어날 때, 정보량은 겹치는 부분이 없으므로 그냥 더해주면 되고, 확률은 아까 배운대로 서로 곱해주면 됩니다. 이때 정보량을 나타내는 함수 h를 그림상에서는 f라고 적었습니다. 그렇다면, f는 무슨함수 일까요? 함수 f는 단조감소함수 이어야하고, 곱셈연산이 덧셈으로 바뀌어야합니다. 우리는 이러한 함수를 이미 알고 있습니다. log함수의 성질을 고려하면 해당 조건을 잘 만족시킵니다. 따라서 h(x)를 log함수로 정의합니다. 그렇다면 log함수의 밑이 2이고, 앞에 부호가 –인 이유가 무엇일까요? 이는 log함수의 그래프 개형을 보면 알 수 있습니다. 단조감소함수가 되기위해서 –를 앞에 붙였습니다. 다음으로 밑이 2인 이유는 컴퓨터는 비트연산을 하기 때문입니다. “비가 온다.”라는 정보를 컴퓨터가 이해하려면 string으로 정보를 받는것보다 0 혹은 1 이진수로 받는 것이 컴퓨터 측면에서는 훨씬 유리합니다. 따라서 정보를 효율적으로 전달하기 위해 비트 단위로 정보를 송출합니다. 여기까지 이해하셨으면 Entropy를 이해하기까지 얼마 남지 않았습니다. 어찌 보면 당연한 내용을 길게 풀어서 설명하였는데, 용어에 익숙해지지 않으면 어려워질 수 있으므로 자세하게 설명하다 보니 글이 길어졌습니다.

해당 그림은 예시입니다. 해가 동쪽에서 뜰 확률과 서쪽에서 뜰 확률을 예시로 들었습니다. h와 p가 어떤 식으로 적용되는지 잘 살펴보시기 바랍니다. 여기서 –log2(p)가 아직도 어색하시다면, 앞에 내용을 다시 읽고 오시길 추천드립니다.
해당 식에서 한번 통신에 보내는 평균 정보량은 얼마일까요? 각각의 정보량에 확률을 곱한값을 총합 해주면 됩니다. 이를 식으로 나타낸 것이 위의 나와 있습니다. 총합을 해주기 위해 시그마연산이 들어가고, 위에서 배운 내용에 확률을 곱한 것뿐입니다. 그리고 그 값이 바로 Entropy입니다. 즉, 한번 보내는 정보량의 기대치, 평균 정보량, Entropy 표현방식에 차이가 있을 뿐 다 같은 의미입니다. 혹시라도 열역학을 공부하신 분이 계시다면 열역학에 나오는 entropy도 같은 맥락입니다. 다만 information theory에서 의미하는 entropy는 수식적으로 조금 다르므로 혼동을 야기할 수 있습니다. 그러므로 우선은 information theory관점에서의 entropy만 생각합시다. 여기까지 따라오셨으면 KL-divergence를 이해하기까지 첫 스텝을 무사히 이해하셨습니다.
위에서 너무 이론적인 내용만 다룬거 같아서 이를 entropy를 계산하는 예시를 통해 좀 더 알아보겠습니다.
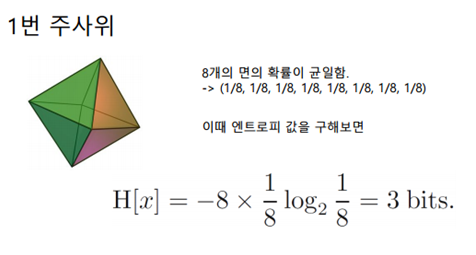
정팔면체의 주사위가 있다고 해봅시다. 2의 n승으로 나누어떨어지므로 정팔면체로 가정했습니다. 이 주사위에서 각각의 면이 나올 확률은 동일합니다. 이때의 엔트로피값은 아까 구한 식을 이용하면 위의 그림처럼 됩니다. 즉 3 bits이며 이는 곧 정보를 나타내기 위한 최소한의 bit량을 의미하기도 합니다. 이와 같은 이론은 Shannon이란 사람에 의해 제안되었으며, 정보를 나타내는 최소한의 값을 정의할 수 있단 점에서 큰 의미를 갖습니다.

이번 예시에서는 uniform하지 않은 주사위에 대해 알아보겠습니다. 위에서와는 다르게 각면이 나올 확률이 서로 다릅니다. 엔트로피의 정의에 의해서 엔트로피값을 구해보면 2bits가 나옵니다. 이를 코드상으로 0, 10, 110, 1110, 111100… 총 8개의 값 나타냈습니다. 이 코드들의 길이의 평균값은 코드길이x확률로 나타낼 수 있습니다. 그리고 그 값은 2가 나옵니다. Entropy와 같은 값이 나왔는데 이를 entropy혹은 average code length의 lower bound라고도 할 수 있습니다. 어떤식으로 코드를 구성하던지간에 lower bound보다 낮게 나올 수는 없습니다. 사실상 위에서 했던 얘기를 조금 다른 말로 반복하고 있습니다. 이로써 복습의 의미도 있고, 다양한 용어에 좀 더 익숙해 질 수 있습니다.

이전까지는 random variable이 discrete 한 variable에 대해서만 다루었습니다. 그런데 Continuous 한 경우에 대해 알아보겠습니다. 즉, 0~1 사이의 값이 어떤 값이든 뽑힐 수 있는 variable이라고 하겠습니다. 이는 곧 델타가 0으로 갈때의 극한값으로 나타낼 수 있습니다. 또한, 시그마를 적분기호로 바꿔줄 수 있게 됩니다. 이때 로그가 자연로그로 된 것은 표현방식의 차이입니다. 로그 밑이 이전예시처럼 2이여도 상관없습니다. 이렇게 해서 entropy 계산식을 구했습니다. 이는 위에서 언급했듯이 average code length의 lower bound를 의미하기도 합니다.
그렇다면 entropy를 maximzie하는 분포는 무엇일까요? descrete한 variable의 경우에는 uniform한 분포가 entropy를 maximize합니다. Countinuous variable의 경우 Guassian 분포가 entropy를 maximize합니다. 예를들어 이전에 봤던 ’해가 동쪽에서 뜬다‘ 예시의 경우 한쪽에 확률이 몰려있으므로 entropy가 아주 작습니다.
이제 드디어 KL divergence를 이해하기 위한 배경지식 학습을 마쳤습니다. 앞의 내용들중에 이해가 가지 않는 부분이 있다면 정확히 이해하고 넘어가시길 권장 드립니다. KL divergence에 대한 설명은 앞의 내용을 완벽하게 이해하고 있다는 가정하에 진행하겠습니다.

승은이는 바보라고 가정합시다. Uniform한 정사면체의 주사위를 던졌을 때, 각 면이 나올 확률은 1/4입니다. 그러나 승은이는 이를 잘못 생각하였습니다. 이에 자주 일어나는 일은 짧게 코딩하고, 자주 일어나지 않는 일은 길게 코딩하였습니다. 이에 대해 average code length, 즉 entropy를 계산해보겠습니다.

정확한 확률 p를 알고 계산한 entropy는 2가 나오고, 승은이가 추정한 확률 q로 계산한 entropy는 2.25가 나왔다. 즉, 0.25만큼의 cost가 발생한 것이다. 바로 이 0.25가 KL-divergence가 된다. Machine learning에서 KL-divergence가 자주 등장하는 이유는 여기에있다. 실제 모델에서 확률이 p이고 내가 설계한 확률이 q일 때, p와 q사이의 차이를 줄이기 위해 loss 함수를 정의하고 이를 학습시킨다.

위의 내용을 일반화시켜서 정리하면 위의 그림과 같다. cost는 각 entropy의 차이로 정의할 수 있고, 이는 log연산하여 1개의 항으로 축소시킬 수 있다. 이를 continuous한 variable로 확장하면 적분기호를 이용하여 나타낼 수 있다.
이로써, entropy와 KL divergence에 대해 알아보았습니다. 그렇다면 특징에 대해서도 알아봅시다.

KL divergence는 p|q와 q|p가 같지 않습니다. 그 이유는 대칭성이 없기 때문입니다. 즉, 추정값과 실제값 간의 방향성이 있어서 바꿨을 때 같지 않습니다. 또한 KL divergence는 항상 양수이며, 이는 log 함수의 convexity를 이용하여 증명 가능합니다.

앞에서 KL divergence와 entropy에 관해서 이야기했습니다. 그렇다면 Cross-entropy는 무엇일까요? 위의 내용을 정확히 이해했으면 아주 쉽습니다. KL divergence를 정의할 때, 앞의 term을 cross entropy라고 합니다. 이는 곧 H(p, q)라고 표기할 수 있습니다. 위의 그림을 보시면 좀 더 이해가 쉬우실 겁니다. 그렇다면 classification 문제를 해결할 때, 왜 cross-entropy loss를 사용할까요? 이유는 KL divergence의 minimum 값을 구하기 위해서는 미분을 해야 하기 때문입니다. KL divergence 식에서 p는 이미 정해진 값이고 q는 학습을 통해 구해야 하는 값입니다. 양변을 미분하면 오른쪽의 term은 p로만 구성된 상수항 취급되어 사라지게 됩니다. 따라서 KL divergence를 minimize하는 것과 cross-entropy를 minimize하는 것은 결국 같게 됩니다.

마지막으로 mutual information에 대해서만 설명하고 마무리 하겠습니다. 식으로 볼때는 상당히 어려워 보이지만, KL divergence를 이해하면 쉽게 이해할 수 있는 내용이므로 같이 넣었습니다. x랑 y라는 확률변수가 있을 때, 서로 독립이라고 해봅시다. 그때의 동시에 일어날 확률은 각 확률의 곱셈으로 정의됩니다. 그러나, 독립이 아니라면 어떻게 될까요? 독립에 가까울수록 두 확률의 곱셈에 가까워질 것입니다. 이 차이를 KL divergence를 이용해서 둘의 거리를 계산하는 식이 위에 나온 식입니다. KL divergence p(x,y)와 p(x)p(y)의 거리를 계산하면 이 둘이 얼마나 가까울지 알 수 있습니다. 이를 mutual information이라고 합니다. 만약 p(x,y)와 p(x)p(y)이 같다면 log1 = 0이므로 0이되며 이는 서로 일치함을 나타냅니다. Mutual information또한 KL divergence의 일환이므로 항상 양수이며, 서로 같을 때 등호가 성립합니다.
이를 통해 Entropy, cross-entropy, KL divergence, mutual information에 대해 알아봤습니다. 궁금하신 점은 댓글로 질문 남겨주시면 답변해드리겠습니다.
평균 정보량(엔트로피) = 정보를 나타내기 위한 최소 bit량, average code length의 lower bound 인 것인가요?
예시 중간중간 코딩 방법에 대해 자주 발생하는 사건에 대해 적은단위로 코딩한것 같은데 1/2, 1/4, 1/8, 1/8의 발생확률을 0, 0, .01, 10이 아닌 0, 10, 110, 111로 코딩되는지 알 수 있을까요..?
일단 첫번째 질문에 대한 답변입니다. 말씀하신 내용이 맞습니다.
두번째 질문은 0, 0, .01, 10 이 부분이 잘 이해가 되지 않습니다. 하지만, 아주 예리하신 질문입니다. 0, 10, 110, 111은 huffman coding에 의하여 정의됩니다. 해당 내용은 리뷰에서 다루지 않았습니다. huffman code를 정의하기위해 haffman tree를 그리는 과정은 아직 공부가 부족하여 나중에 기회가 되면 다루겠습니다.
상세한 정리 감사합니다!
아닙니다. 쉬운 내용이지만 조금이나마 도움이 되셨으면 좋겠습니다.
cross entropy loss는 자주 사용해왔는데, KL-divergence loss는 적용되는곳이 어디가 또 있나요?
machine learning 에서도 classification 문제에 많이 활용되는걸로 알고있습니다. KL divergence loss하고 cross entropy loss를 구분해서 쓰는 이유에대해서는 제가 참고한 해당영상에서 빠진부분이고, 아직 학습하지 않아서 저도 잘 모르겠습니다. 다만, KL divergence나 cross entropy loss나 둘다 q를 학습한단 맥락에선 동일한걸로 알고있습니다.