이번 리뷰는 네이버 초청 세미나 내용 중 Embedding Expansion에 대해서 정리해보고자 합니다. 정말 유익한 세미나였음에도 불구하고, Metric Learning에 대해 이제 막 공부하는 단계인지라 해당 세미나의 내용들을 완벽히 이해하지는 못하였습니다. 그래서 해당 리뷰에서 최대한 이해한만큼 적어보고자 합니다.
Metric Learning
먼저 Metric Learning이란 쉽게 말해서 물체를 표현하는 vector(embedding)들이 얼마나 유사한지를 vector들 간에 거리 정도로 표현하게끔 학습하는 것을 의미합니다.
즉 두 물체가 서로 동일한 class 일수록 두 물체를 표현하는 vector들 사이의 거리가 가까울 것이고, 반대로 서로 다른 class이면, vector들 사이의 거리도 멀어지는 것입니다.
이러한 metric learning의 장점은, 학습 데이터에서 한번도 보지 못한 영상이 test로 들어왔을 시에도, object를 표현하는 vector 간에 거리를 이용해 해당 test 영상의 class를 근사할 수 있는 것입니다.
Pair based Metric Learning loss
이러한 Metric Learning을 하기 위한 loss로는 크게 pair based loss와 proxy based loss로 나뉘는데, pair based loss 안에는 또 아래와 같은 방식들이 존재합니다.

- Contrastive Loss
- Triplet Loss
- N-pair Loss
- Lifted Structured Loss
- Multi-Similarity Loss
먼저 Contrastive Loss는 Metric Learning의 근본적인 목적에 맞게끔 설계된 loss입니다. 바로 positive는 더 가깝게, negative는 더 멀리 가게끔 학습하는 것입니다.
이러한 Contrastive Loss에서 조금 더 발전한게 바로 Triplet Loss입니다. Contrastive Loss와는 컨셉이 같으나, anchor 한번에, positive와 negative를 동시에 비교해서 계산하는 것을 의미합니다.
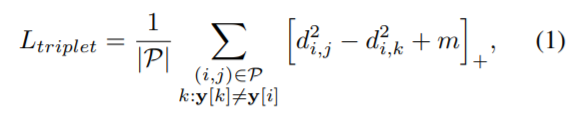
Triplet loss에 대한 수식은 위와 같습니다. d^{2}_{i,j} 는 anchor와 positive의 유클리디안 거리를 나타내는 것이며, 뒤에 d^{2}_{i,k} 는 anchor와 negative의 유클리디안 거리를 나타내는 것입니다.
즉 positive의 유클리디안 거리 값은 부호가 + 이므로 작으면 작을수록, negative의 유큘리디안 거리 값은 부호가 – 이므로 크면 클수록 Triplet loss값이 작아지는 것을 확인할 수 있습니다.
Triplet loss에서 하나의 negative class만을 보았다면, N-pair loss는 모든 negative class(N-1 개)를 보면서 학습하는 것입니다.(물론 positive는 하나 입니다.)
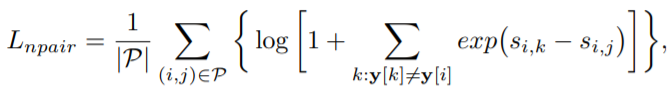
s_{i,k}, s_{i,j} 는 각각 anchor transpose벡터에 대해서 positive와 negative를 행렬 곱한 것으로, 임베딩 점들의 유사성을 표현한 것입니다.
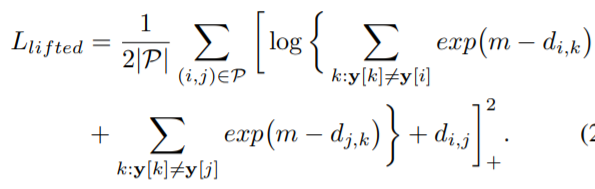
위에 수식은 Lifted Structured Loss 수식입니다. 해당 loss는 anchor와 하나의 positive 끼리는 최대한 가깝게 위치하도록하며, 나머지 모든 negative와 그에 대응하는 positive들 끼리는 고정된 마진 값보다 더 멀리 위치하게끔 설계되어있습니다.
마지막으로 Multi-Similarity loss는 negative 뿐만 아니라, positive도 2개 이상을 보게끔 설계되었습니다.
이러한 pair based loss는 매우 직관적인 방법이지만, 단점이 존재합니다.바로 학습 방식이 너무 복잡하다는 것입니다.
먼저 pair들의 조합(경우의 수)가 너무나 많아지다 보니 학습해야할 데이터가 매우 많고 복잡하며, 데이터의 label로 positive와 negative를 어떻게 분류할 것인지에 대한 기준 역시 애매합니다. 그래서 positive와 negative의 분류를 어떻게 하느냐에 따라 학습 성능도 크게 나타납니다.
초청 세미나에서 들었던 논문은 이러한 metric learning의 문제점, 즉 어떻게 하면 기존의 pair based loss 방식을 더 잘 학습시킬 수 있을지에 대한 방법론들을 제안합니다.
Embedding Expansion
그럼 본격적으로 Embedding Expansion 논문에 대해서 정리하고자 합니다. 해당 논문의 동기와 contribution은 간략히 말하면 아래와 같습니다.
- 동일한 metric learning loss를 사용하더라도, 어떠한 sampling 기법을 사용했느냐에 따라서 성능의 차이가 크게 차이난다.
- 기본적으로 Hard sample mining 기법을 사용하는데, 이 기법은 소수의 hard sample에 대해서 학습하다보니, 다수의 easy sample에 대해서는 무시해버린 채 hard sample에 모델이 편향되는 단점이 존재한다.
- ‘2’번의 문제를 해결하고자 easy sample을 이용하여 합성(synthesis) hard sample을 만드는 generator 방법론들이 제안됐다.
- 하지만 이러한 generator도 일종의 네트워크기 때문에, 모델의 크기가 커지면서, 학습 시간, 메모리, 속도 등의 측면에서 단점이 존재한다.
- 이를 해결하고자 해당 논문에서는 단순한 linear interpolation을 통해 합성 hard sample을 만드는 방법론을 제안한다.
먼저 embedding expansion은 위에서 설명한 pair based loss에 사용 가능합니다. 논문에서는 이 embedding expansion을 data augmentation이라고 표현합니다.
이 이유로는 두 original embedding을 통해 linear interpolation으로 합성 임베딩을 생성하는데, 꽤나 많은 양의 임베딩을 생성하여 학습하다보니 augmentation method라고 합니다.
Synthesis embedding generation
먼저 합성 임베딩을 생성하는 방법에 대해서 알아봅시다.
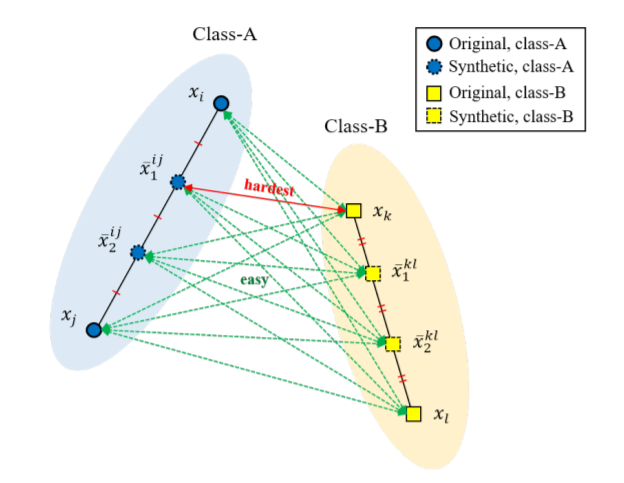
각 클래스에서 두 개의 original embedding을 추출한 다음, 해당 임베딩들을 지나는 직선에 내분점으로 합성 임베딩을 생성합니다.
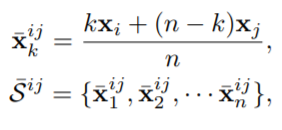
x_{i], x_[j} 는 어떤 class 내의 original embedding들을 의미하며, k에 따른 내분점으로 생성된게 x bar입니다. 그리고 이러한 내분점들의 집합이 2번째 수식인 S bar 입니다.
그럼 왜 내분점을 이용해서 합성 임베딩을 생성할까요? 논문에서는 직관적으로 봤을 때, 어떤 class 내에 original embedding을 잡아서 내분되는 point를 뽑으면, 해당 point는 original embedding과 동일한 class일 확률이 높다고 말합니다.(물론 실험적으로도 결과를 확인했다고 합니다.)
내분점을 이용한 합성 임베딩 생성 기법의 장점은 크게 3가지가 있다고 합니다.
- 각 class의 내분점 끼리의 거리를 계산함으로써, high dimensional space 상에 거리 계산보다 연산량이 훨씬 줄일 수 있는 장점이 존재.
- 합성 임베딩의 label이 original embedding과 동일한 class일 확률이 높다.
- 단순한 linear interpolation으로 합성 임베딩을 만들다보니, 메모리나 속도, 연산량에서 큰 강점을 보인다.
먼저 첫번째 장점에 대해 간략히 설명하자면, 기존에 hardest negative pair 구하기 위해서 각 class로부터 각 pair 끼리의 거리를 계산하였습니다. 이를 통해 가장 짧은 거리를 가지는 pair를 hardest negative로 선정했었죠.
하지만 high-dimensional space 상에 존재하는 embedding vector들 끼리의 거리를 계산하는 것은 생각보다 computing cost가 많이 든다고 합니다.
하지만 논문에서 제안하는 방법을 사용하면, 각 class 의 내분 점들 사이의 거리를 계산하기 때문에, computing cost를 줄일 수 있다고 말을 하는데, 사실 이 부분이 이해가 잘 가지는 않네요… 혹시 이에 대해 아시는 분은 댓글로 설명해주시면 감사하겠습니다.
두번째 장점에 대해서는 다음과 같습니다. 먼저 이전 방법론에서는 합성 임베딩의 lable을 부여하기 위해, fc layer와 softmax 기법을 사용하곤 했었습니다.
하지만 내분점으로 생성하는 임베딩은 기하학적인 관계를 고려하였기 때문에, softmax 같은 기법 없이도 충분히 label의 확실성을 보장한다고 합니다.
마지막으로 3번째 장점은 위에서 하도 설명을 많이 해서 넘어가도록 하겠습니다.
Hard Negative Pair Mining
합성 임베딩을 생성했다면 이제는 hard negative pair mining을 할 차례입니다. Hard pair mining은 오직 negative에 대해서만 수행되며, original points는 positive pair에 사용됩니다.
그 이유는 original point와 synthetic points 간에 hard positive pair mining(hard negative pair와는 다르게, 두 점들의 distance가 가장 먼 pair를 hard positive로 선정)를 진행하면, synthetic points들은 결국 두 original point 사이에 내분점으로 만들어진 점들이기 때문에 hard positive pair mining의 결과값으로는 항상 original point들의 쌍으로만 이루지기 때문입니다.
Experiments
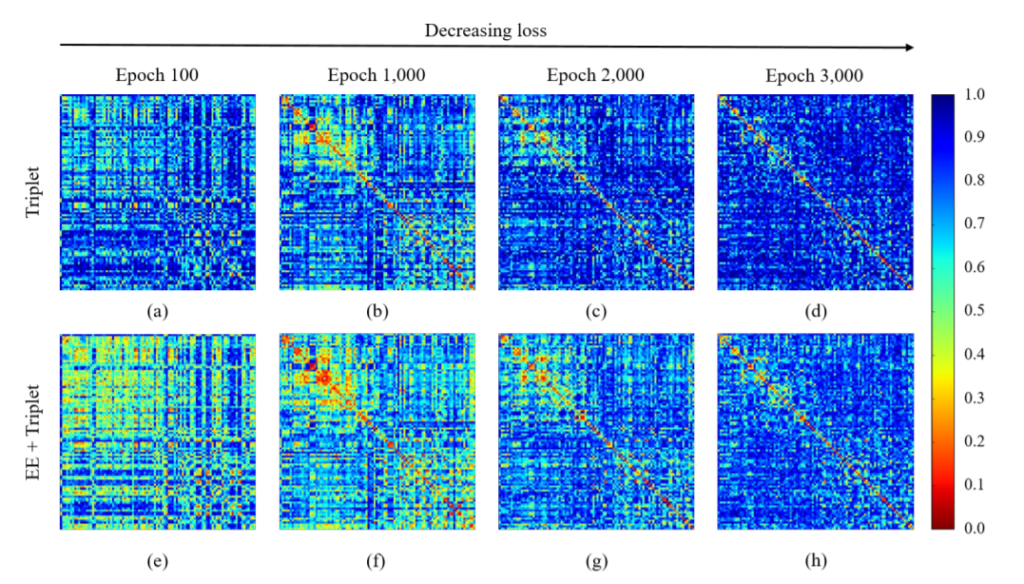
위에 그림은 Embedding Expansion(EE)를 추가한 Triplet loss와 기존 base Triplet loss를 비교한 그림으로, 각각의 heat map에서 대각선 영역이 positive pair의 distance, 그 외에는 negative pair의 distance를 의미합니다.
해당 그림에서 알 수 있는 것은, EE를 붙인 loss의 heat map이 훨씬 yellow~red 영역에 가까운 것을 확인할 수 있는데, 이러한 yellow~red 영역은 더 짧은 pair distance를 의미합니다.
즉 EE를 추가했을 경우 triplet loss 단독으로 사용했을 때 보다 더 많은 hardest negative pair가 생성되는 것을 확인할 수 있습니다.
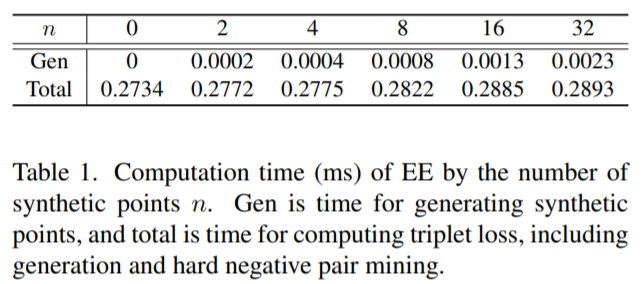
아래 표는 embedding expansion을 통해 합성 임베딩을 만드는 시간을 나타낸 것입니다. 임베딩을 32개를 만드는데, 0.0023 ms 걸리는 것으로, 기존 base triplet loss가 0.2734 ms 걸린다는 것을 감안했을 때, EE를 적용하는 것은 매우 작은 시간이 소요된다는 것을 확인할 수 있습니다.
속도는 빠르면서, 성능은 다른 생성 방법론들(DAML, HDML)에 비해 좋거나, 밀리지 않는 모습을 확인할 수 있습니다.
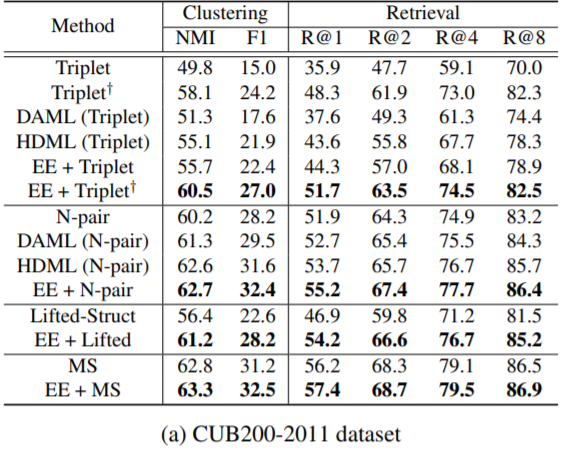
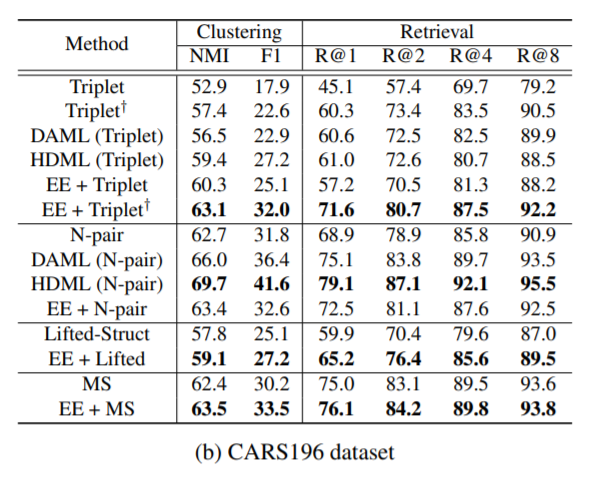
기존에 임베딩을 합성하는 다른 방법론들(HDML, DAML)과 Embedding Expansion 방법론의 속도를 비교하는 표가 논문에 있었으면 하는데, 없어서 조금 아쉽습니다만, 해당 논문 덕분에 Metric Learning에 대한 전반적인 이해부터 최근 이슈가 무엇인지에 대해 꼼꼼히 알 수 있어서 좋았습니다.
세미나를 발표해주신 두 연구원 님과, 이런 기회를 마련해주신 교수님께 감사인사 드립니다.