앞선 리뷰에 이어서 진행되는 글 입니다:)
1. background activation map
본 논문에서는 기존의 CAMs 뿐만 아니라 background activation map도 구한다 구하는 식은 [수식1]과 같다. 이때 \alpha 는 1이상의 hyper-parameter이다.
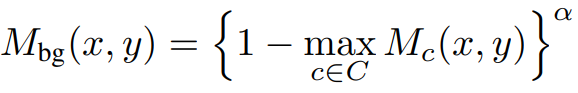

2. AffinityNet
AffinityNet 은 이미지에서 class-agnostic한 인접 pixel 간의 관계를 예측하기 위한 것으로 이는 뒤에 소개할 random walk의 transition probabilities로 사용된다. AffinityNet 의 최종 결과값은 f^{aff} 이며, f^{aff} 의 i^{th}번째, j^{th} 번째 특징의 semantic affinity는 [수식2]와 같이 L_{1} 거리로 나타낸다.
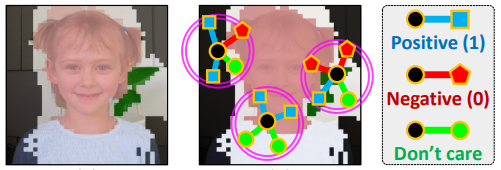
[그림2]의 AffinityNet을 학습시키기 위하여 W_{ij} label이 필요하다. 그러나, 논문에서 제안하는 image-level labels을 이러한 라벨로 바로 이용하기에는 어려움이 있다. 논문은 AffinityNet을 학습하기 위하여 CAMs을 이용한다. activation map은 [그림1]과 같이 (pixel level label 보다)비교적 세밀하지 않으므로 논문은 확실한 영역(background인지 object인지)을 구분하여, 그 영역에서만 sample을 취하는 방식을 이용하고자 했다.
2.1. W_{ij} label 생성하기
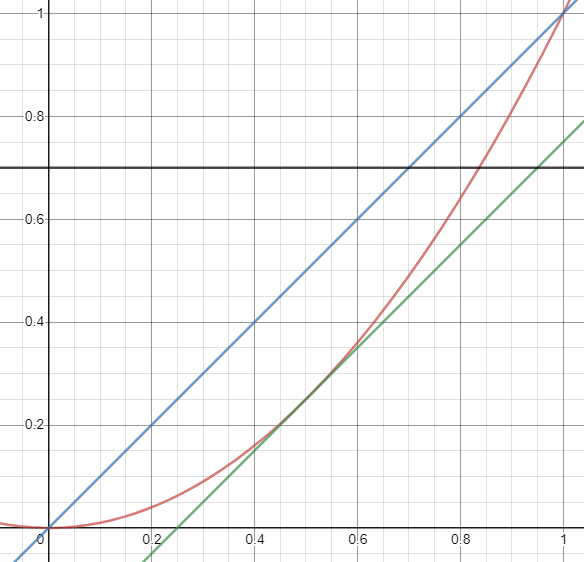
먼저, [수식1]의 \alpha 를 감소시킴으로서 M_{bg} 를 증폭시킨다. 예를들어 \alpha=2 라면 그림3의 붉은색 그래프, \alpha=1 라면 그림3의 파란색 그래프, 일 때 역치가 0.7 (검은색 그래프)라면 \alpha=1일 때, 더 많은 영역 (().7-1.0)이 배경 class로 지배될 수 있다. ([수식 1]의 중괄호 내부값은 0이상 1이하 이므로)
둘째로, dCRF를 적용하여 CAMs을 refinement한다 이는 후처리적 방식으로 CAMs을 더욱 세밀하게 (물체의 boundary를 따르도록) 한다. 이후, 증폭된 M_{bg}를 포함한 classes activation score (object score + weaken M_{bg} )중 가장 높은 값을 pixel level로 한다. 남은 영역 (증폭된 M_{bg} 가 가장 큰 영역)은 확신할 수 없는 neutral 가 된다. 위의 과정을 통하여 불완전한 CAMs을 이용한 W_{ij} label 을 생성하였다.
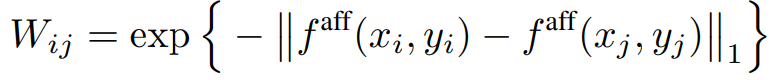
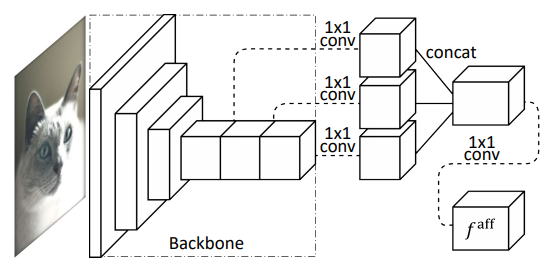
AffinityNet의 결과가 random walk의 transition probabilities 로 사용된다는 것으로 보아 아래의 결과는 인접한 픽셀이 더 이동하기 높은 확률 값으로 쉬운 영역은 밝게, 이동하기 어려운, 물체의 경계라인에서는 은 낮은 확률값으로 어둡게 나타나는 것으로 해석하였다.

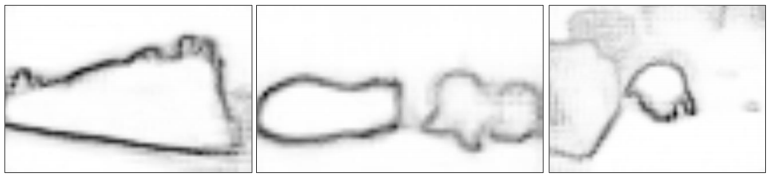
3.random walk
random walk는 Markov Chains의 특별한 케이스로, 움직임의 가장 단순한 시물레이션 중 하나이다. random walk 란 임의의 단계로 정의되는 경로이며, Image segmentation 분야에서는 주로 label(ie., “object” 또는 “background”)을 결정하는 데 사용된다. RWR(random walk with restart) 알고리즘은 이미지 분할을 위한 알고리즘인데, 이미지 분할을 위한 대회식 방법으로 처음 소개되었다고 한다. 이처럼 random walk가 이미지 분할 영역에서도 사용됨을 알 수 있으나, 논문에서 다루는 부분은 RWR가 아닌 RW(random walk)이므로 이를 소개하겠다.
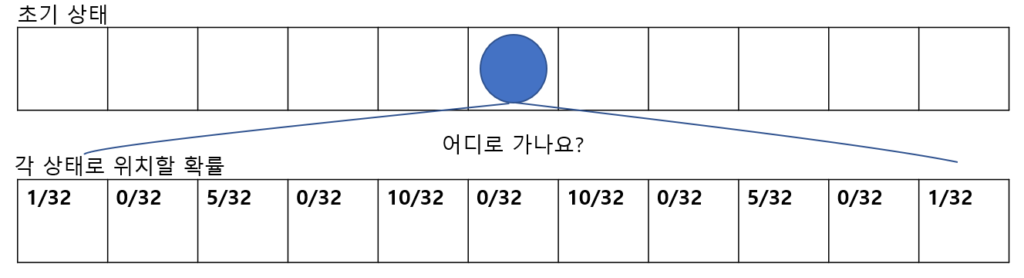
랜덤워크위 상위 개념인 마르코프 체인은 각 시행의 결과가 바로 앞시행의 결과에만 영향을 받는 확률적 시행을 말하며, 랜덤워크는 한 지점에서 사람이 일정한 거리 a 만큼 n회 움직일 때, 이동 이후 출발점으로 부터 거리가 r~r+dr 사이에 있을 확률을 의미한다.
예를 들어,
파란 walker가 초기상태의 중심에 위치할 때 1만큼 5회 움직일 때 각 위치에 있을 확률은 [그림6]과 같다. 그림6의 예시는 오른쪽과 왼쪽 각 이동이 같은 확률을 갖을 때의 최종 결과이다. 논문에서는 각 이동이 동일한 확률을 갖는 것이 아닌 예측한 semantic affinities 를 이용하여 segmentation을 진행하는 것으로 이해하였다. 이에대한 내용은 추가적인 공부 이후 보충하겠다.