이번에 제가 다룰 주제는 Robotics입니다. Robotics는 로봇을 다루기 위해서는 필수적으로 알아야 할 학문입니다. 기계과 곽관웅 교수님의 교안과 강의를 참고했으며, http://www.kocw.net/home/search/kemView.do?kemId=1358399 를 들어가시면 강의를 수강하실 수 있습니다. 교안은 저작권문제로 공개되어있지 않습니다. 따라서 교안 중 학습을 하며 중요하다고 생각되는 내용 일부만 발췌해왔으며, 로보틱스의 전체적인 흐름을 소개해드리겠습니다.

위의 내용을 읽어보시면 기본적인 용어가 정리되어 있습니다. 이는 예시를 통해 쉽게 이해할 수 있습니다. 로봇팔이 있다고 했을 때, manipulator는 로봇팔이 됩니다. End-effector는 쓰임에 따라 로봇팔 끝에 장착할 수 있는 장치라고 보시면 됩니다. (예시: 드릴, 집게, 용접)
로보틱스에서는 이러한 manipulator와 end-effector 사이의 관계를 중요하게 생각합니다. 즉, x와 theta 사이의 관계가 로보틱스에서 다루게 될 주 관심사입니다. 여기서 x와 theta는 쉽게 말해서 로봇팔에 들어가는 서보모터와 end-effector가 위치해야 하는 곳의 좌표와 방위입니다. 우리는 이 관계를 알아야 로봇을 자유자재로 제어할 수 있습니다.

위의 내용을 쉽게 정리하면 아래 두줄로 요약할 수 있습니다.
forward kinematics
inverse kinematics
이를 이해하기 위해서는 우선 kinematics와 kinetics의 차이를 알아야 합니다. 이는 동역학에 나오는 개념과 같습니다. Kinetics는 위치에너지, 운동에너지, 마찰 등 힘에의한 역학적 요소를 고려하는 반면 kinematics는 velocity, position등 위치적인 요소만을 고려합니다. 로보틱스에서는 로봇의 위치제어가 주 관심사기 때문에 kinematics가 주를 이룹니다. 이때 를 가지고 X를 추정하는 것을 forward kinematics(정 기구학) 그리고 그 반대를 inverse kinematics(역 기구학)라고 합니다.
그렇다면, 두 개중 어떤 것이 더 중요할까요? 그건 바로 inverse kinematics입니다. 이유는 (관절변수)는 모터의 input voltage를 다르게 줌으로써 비교적 자유자재로 바꿀 수 있기 때문입니다. 다른 말로 값을 자유자재로 조정해서 로봇의 end-effector의 위치를 원하는 곳으로 위치시킬 수 있습니다. 그리고 그 end-effector의 orientation(방위)를 바꿈으로써 로봇이 원하는 임무를 수행할 수 있도록 합니다. 이때 end-effector의 방위를 바꾸기 위해 별도의 서보모터를 사용합니다. 직각좌표계 상에서 x, y, z 3의 degree of freedom (DOF)를 가지려면 최소한 3개의 서보모터가 필요합니다.
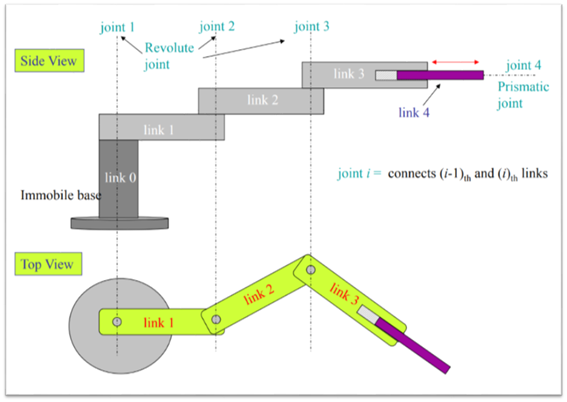
이번에는 가장 naive한 로봇의 형태에 대해 살펴보겠습니다. 로봇은 link와 joint로 이루어져 있습니다. joint는 병진운동만 하는 prismatic joint가 있고, 회전운동만 하는 revolute joint가 있습니다. 그리고 이를 줄여서 일반적으로 P, R 기호로 나타냅니다. 각각의 link 번호와 joint에 numbering하는 방법에 대해서는 뒤에서 다루겠습니다. 여기서는 그냥 link와 joint가 어떤 식으로 이루어져 있고, 고유의 번호를 가진다는 정도만 이해하고 넘어가시면 되겠습니다.

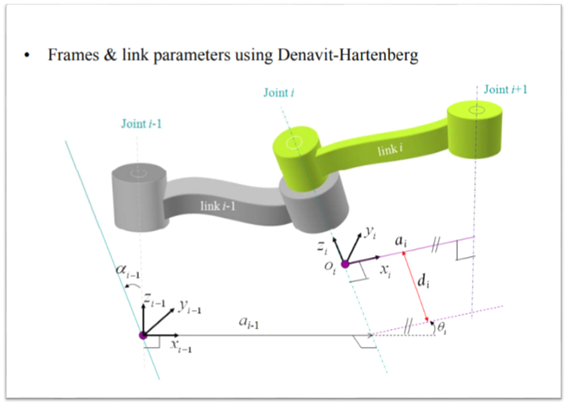
x와 theta의 관계를 알기 이전에 가장 기초가 되는 작업은 로봇의 좌표를 설정하는 것입니다. 좌표계를 설정하려면 우선 link parameter들이 무엇인지 이해해야 합니다. 위에 나온 link length, link twist angle, link offset, joint angle의 정의를 읽어보시고, 아래에 나오게 될 그림과 비교해가시면 이해하는 데 어려움이 없을 거라고 생각됩니다. 위의 link parameter의 정의와 좌표계를 세우는 방법을 외우지는 못하더라도 보고서라도 좌표계를 세울수 있으면 충분하다고 생각합니다. 좀 더 공부해보시고 싶으신 분들은 로보틱스 교재를 찾아보시면 좌표계를 세우는 문제들이 나와 있습니다. 해당 자료를 읽으면서 실제로 좌표계를 세워보고, 문제의 정답과 비교해가며 공부해보시는 것을 추천드립니다. 이번 x-review에서는 그중 한 문제를 실어 놨습니다.

좌표계를 세우는 데는 Denavit-Hartenberg(DH) 규약이 가장 대표적입니다. Link parameter에 대해 이해를 한 다음 해당 자료를 참고하시면 좌표계를 세울 수 있습니다. 아래에 예시문제를 수록해두었습니다. 문제를 프린트하신 다음 직접 좌표계를 세워보시는 것을 추천해 드립니다. 글의 끝에 정답을 수록해두었으니, 직접 해보시고 정답과 비교해보시면 학습에 도움이 될 겁니다.
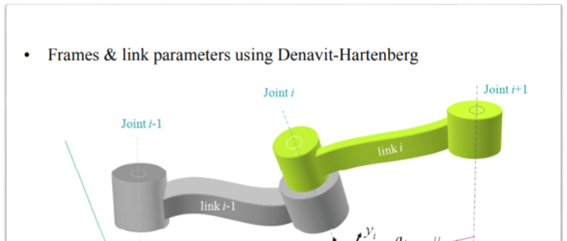

이제 좌표계를 세우는 기본작업을 배웠으니, 본격적으로 kinematics에 대해 배워보겠습니다. 로봇의 kinematics는 translation과 roation으로 나뉩니다. 이 개념은 컴퓨터비전의 affine transformation과 흡사하다고 생각합니다. 다만, 로봇은 일반적으로 강체이기 때문에 형태 변화가 없습니다. 따라서 scale같은 변환은 불가능하고, rotation이나 translation만 가능합니다. 3 자유도에 대해 rotation은 3 X 3 행렬로 나타낼 수 있고, translation은 3 X 1 vector로 나타낼 수 있습니다. 이를 합치면 3 X 4 행렬이 됩니다. 행렬계산을 할 때 정방행렬이 계산하기에 편리하므로 3 X 4 행렬을 4 X 4 행렬로 만들어줍니다. 이때 추가해주는 행의 원소들은 항등식이므로 사실상 쓸모없는 식이 됩니다. 다만 정방행렬의 형태를 만들기 위해 추가한 항입니다.
이렇게 해서 나오게 된 4X4 matrix가 최종적 위치와 방위를 결정하는 transformation matrix가 됩니다. 이때의 matrix의 원소는 link parameter들로 이루어져 있습니다. Link parameter들을 자유자재로 가져다 쓰려면 table로 정리하는 것이 편합니다. 따라서 DH 규약에 따라 좌표계를 세운 뒤에는 DH table을 만들어 두는 것이 좋습니다. 이해를 돕고자 아래 DH table의 예시를 구글에서 가져왔습니다.

이상으로 X와 theta의 관계 중 forward kinematics에 대해 알아보았습니다. Inverse kinematics는 정확한 공식이 없고, 간단한 구조에 대해서만 명확한 솔루션이 제시되어있습니다. 이들을 해석적인 방법에의한 솔루션이라고 합니다. 하지만 조금만 복잡해지더라도 솔루션을 도출해내기란 사실상 불가능에 가깝습니다. 그래서 수치해석적인(numerical) 방법으로 접근하기도 합니다. 하지만, 이는 real-time으로 작동을 해야하는 로봇에는 적합하지 않을 수 있습니다. 따라서 real-time으로 로봇을 제어하기 위한 연구가 많이 진행되고 있습니다. 실제 산업현장에 가보면 하루종일 inverse kinematics만 연구하며, Equation of Motion (운동방정식)을 찾으려고 노력하는 연구원분들이 계신다고 합니다. 이러한 점을 고려해 보았을 때, 뒤에서 배우게 될 자코비안은 매우 혁신적입니다. 자코비안은 end effector의 선속도를 주고 각 관절의 각속도를 구하는데 이 각속도를 구한다음 적분을 통해 각도를 구할 수 있습니다. 좀더 자세히는 뒤에서 다루겠습니다.

자코비안을 증명하기 위해서, end-effector의 위치와 방위에 대해 위와 같이 정의해 보겠습니다. 우리는 앞서, X 와 theta 사이의 관계만을 중점적으로 다루었습니다. 이번에 다루는 내용은 velocity에 관한 내용이므로, X와 theta를 각각 시간에 대해 미분한 값입니다. 이를 6자유도 manipulator로 확장하고, X대신 u로 표기하겠습니다. 그리고 theta대신 f로 나타내겠습니다. f는 위에서 배웠듯이, link parameter를 원소로 가지는 함수 형태일 것입니다.

그리고 양변을 t에 대해 미분한다음 chain rule을 적용해 줍니다. 이후 행렬표현으로 바꿔주면 자코비안이 쉽게 증명이 됩니다. 즉 자코비안은 u dot과 q dot 사이의 관계식을 나타내주는 행렬입니다. 자코비안이 중요한 이유는 역행렬에 있습니다. 일반적으로 inverse kinematics는 매우 복잡하지만, 자코비안은 역행렬을 양변에 곱해주면 이를 쉽게 해결할 수 있습니다. 이를 물리적인 의미로 재해석하면, 자코비안의 역행렬을 계산함으로써, 모터의 속도와 end-effector의 속도 사이의 관계를 계산 할 수 있음을 의미합니다. 즉, 모터의 input 전압을 제어함으로써, 원하는 속도로 로봇을 제어할 수 있게 되는 것입니다. 이때, 자코비안의 역행렬은 선형대수적 방법으로 비교적 쉽게 구할 수 있습니다. 따라서 자코비안은 로보틱스에 있어서 매우 중요한 개념입니다.

해당 내용은 위에서 설명한 내용과 일치하므로 한번 복습한다는 느낌으로 가볍게 읽어보시고 넘어가시면 될 거 같습니다.

이미 눈치가 빠르신 분들은 생각했을지도 모릅니다. 자코비안 행렬의 역행렬이 존재하지 않을 때는 해가 존재하지 않는 거 아닌가요? 라는 의문이 생길 수도 있습니다. 네 맞습니다. 해가 존재하지 않습니다. 그리고 그 해가 존재하지 않는 부분을 특이점(singularities) 이라고 합니다. 로보틱스에서는 이 특이점이 매우 중요합니다. 컴퓨터비전을 전공하는 사람으로서도 특이점에 대한 이해가 필요하다고 생각합니다. 이는 안전과도 관련된 문제이기 때문입니다. 때에 따라서 로봇의 mass와 torque가 큰 경우에는 잘못된 설계로 인해 생명을 앗아가는 사고까지도 발생할 수 있고, 실제로 발생사례가 꽤 많이 있습니다. 그중 한 예가 특이점을 고려하지 못한 설계입니다. 특이점에서는 해가 존재하지 않고, 모터를 제어하는 제어기 입장에서는 해를 찾으려고 합니다. 따라서 순간적으로 최대출력까지 올라갈 수도 있습니다. 예를 들어 0.1 m/s의 속도로 제어가 되던 로봇팔이 0.11 m/s로 단 0.01 m/s의 속도를 올리기 위해 순간적으로 최대출력이 들어갈 수도 있음을 의미합니다. 이는 치명적으로 위험할 수 있습니다. 컴퓨터비전 전문가가 로보틱스를 이해하면 좋은점 중 하나가 여기에 있습니다. 자코비안 행렬을 받아서 사용한다고 해도, 특이점에 이해가 없으면 자신이 준 input에 비해 output이 이상하게 나올 수 있습니다. 이때 이러한 이론을 모르면, 디버그를 할 수 없을뿐더러, 인명사고로까지 이어질 수 있습니다.
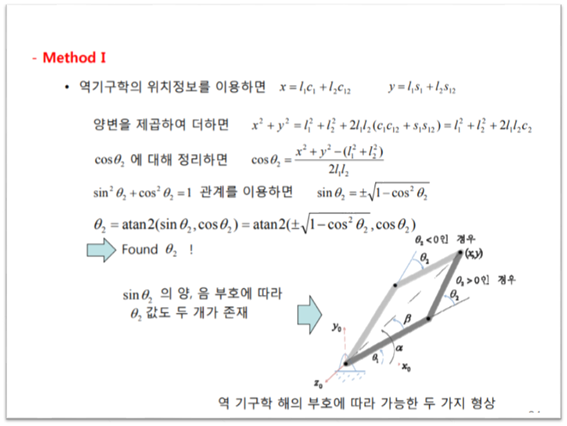
해당 문제는 때에 따라서는 같은 위치로 제어하는 방법에는 2가지 형상이 존재할 수 있음을 보여드리기 위해서 가져왔습니다. 혹은 2개 이상의 솔루션이 존재할 수도 있습니다. 자유도가 높은 로봇팔의 경우에는 무한대의 솔루션이 존재하는 때도 있습니다. 이의 경우에는 trajectory(경로) 설정을 하는 것이 의미가 있습니다. 혹은 일정 경로로 로봇팔이 이동하는 것이 중요한 작업을 할 경우 trajectory를 specify하는 것이 필요합니다. Trajectory 이론과 제어 이론에 대해서는 다음에 기회가 있으면 다뤄보도록 하겠습니다.
< 좌표계 세우기 문제 정답 >
특이점을 고려하지 못한 설계입니다. 특이점에서는 해가 존재하지 않고, 모터를 제어하는 제어기 입장에서는 해를 찾으려고 합니다.
이런한 문제에서 해결책은 무엇인가요?