Optical flow

요새 연구실에서 다른 연구원님들이 video 관련 과제들을 하다 보니 ‘optical flow’ 라는 단어를 종종 듣게 되었습니다. 근데 이 optical flow에 대하여 가볍게 언급만 할 뿐, 중점적으로 다룬 리뷰 글은 딱히 없는 것 같아서, 제 공부도 할겸 이번 기회에 리뷰를 작성하고자 했습니다.

먼저 optical flow는 연속한 두 frame 사이에서 각 pixel이 얼마만큼 이동했는지를 나타내는 Vector Map을 말합니다.

위에서 좌측 그림을 보시면 화살표로 표현이 되어 있는데, 화살표의 방향이 object의 이동 방향을, 화살표의 길이가 이동량을 말하는 것입니다.

하지만 이렇게 화살표로 표현하는 방식은 보시다시피 지저분한 것을 확인하실 수 있는데, 그래서 optical flow 분야에서는 화살표 방식 뿐만 아니라 color를 통해서 물체의 이동 방향 및 크기를 표현하기도 합니다.

우측 그림이 바로 색상을 통해서 이동 방향 및 크기를 표현한 것인데요, 이는 색상을 표현하는 방법 중, RGB가 아닌 HSV 방식을 사용한 것입니다.

HSV에서 H는 색상 종류, S는 색상의 채도(magnitude), V는 명도를 의미하는데, optical flow는 여기서 색상(H)를 통하여 물체의 방향을 표현하고, 채도(S)를 통하여 채도가 진하면 크게 움직인 것이고, 연하면 조금 움직인 것을 표현합니다.

위에 그림을 보시면 7시 방향이 연두색인데, 중앙점을 기준으로 물체가 7시 방향을 향해 나아가면 해당 물체의 색상은 연두색으로 표현이 되고, 반대로 물체가 2시 방향으로 나아가면 색상은 핑크색이 됩니다.

그리고 자세히 보시면 중앙점의 색상이 하얀색에 가까운데, 해당 지점에서 외곽으로 갈수록 색상의 정도가 진해집니다. 즉 물체의 움직이는 정도가 더 크다는 것을 의미합니다.

Optical flow Constraint

optical flow에는 제약조건이 존재합니다. 조건은 상당히 간단한데, 바로 이동하기 전 pixel과 이동 후의 pixel의 intensity 값이 동일하다는 것입니다.

즉 flow vector로 이루어진 pixel에 대해서 이전 프레임에서의 pixel값과 다음 프레임에서의 pixel 값이 반드시 동일해야만 한다는 것입니다.

이를 먼저 수식으로 나타내면 다음과 같습니다.

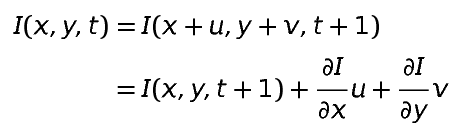
먼저 image의 명도를 I(x,y,t)라고 했을 때, 해당 명도 I를 x,y, 그리고 시간 t에 대한 함수로 놓습니다.그리고 얼마만큼 이동했는지를 표현하는 magnitude를 (u, v)라고 한다면, 기존 I(x, y, t)에 u와 v값을 더해줌으로써 이동 후의 위치를 표현할 수 있습니다.

이제 위에서 설명한 이전 프레임의 명도와 다음 프레임의 명도가 같다는 제약 조건을 만족하기 위해 I(x, y, t) = I(x + u, y+v, t+1)로 표현을 한 것입니다.

여기서 u랑 v를 테일러 급수를 통해 함수에서 벗어나게끔 표현을 하는데, 테일러 급수는 간략하게 말하면 미지의 함수에 대하여 근사 다항 함수로 표현하는 것을 의미합니다.

여기서 한가지 유의하셔야할 점은 테일러 급수는 근사하고자 하는 함수의 전체적인 경향성에 근사하는 것이 아닌, 기준 지점과 그 근처 영역 대해서만 근사를 하는 것입니다.

위에 그림은 sin x 함수를 테일러 급수를 통해 근사한 것입니다. 보시면 아시겠지만, 테일러 급수의 차수가 1차일 때 기준 지점(위에 예시에서는 0)은 sin 함수와 유사하게 근사되었습니다.하지만 기준 지점으로부터 멀어질수록 근사가 잘 안되는 모습을 보실 수 있습니다.

물론 테일러 급수의 차수가 높으면 높을수록 보시다시피 기준 함수의 전체적인 모습과 매우 유사하게 근사되고 있습니다.(P7, P5, P3 순으로 근사의 정확도가 떨어지고 있음.)

optical flow에서는 1차 테일러 급수를 사용하였습니다.

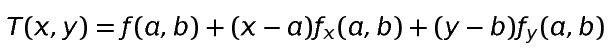
2차방정식의 1차 테일러 급수 표현 식

자 그럼 다시 optical flow 제약 조건 식으로 돌아와서, 좌변에 I(x, y, t)를 우변으로 넘겨서 ~~ = 0 형식으로 식을 정리해 봅시다.

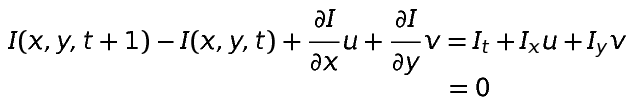
보시면 I_{t}, I_{x}, I_{y} 는 각각 함수 I를 t에 대하여, x에 대하여, y에 대하여 미분했다는 표기입니다. 그래서 깔끔하게 I_{t} + I_{x}u + I_{y}v = 0 로 식이 정리가 됩니다.

제약조건 식이 깔끔하게 정리되는 것은 좋지만 문제가 하나 발생합니다. 바로 주어진 방정식은 하나인 반면, 우리가 구해야 할 미지수 u, v는 2개인, UnderDetermined 상황입니다. 이러한 문제를 해결하고자 여러가지 알고리즘들이 존재하는데 아래에서 해당 알고리즘들을 설명하려 합니다.

Lucas-Kanade Method

optical flow에서 가장 보편적인 알고리즘은 바로 Lucas-Kanade 알고리즘입니다. Lucas Kanade 알고리즘은 아래 수식과 같이 optical flow의 제약조건이 최소화하는 방향(0이 되게끔)으로 동작하여 u랑 v를 구하게 됩니다.

그런데 여기서 시그마 아래부분에 N(x)는 무엇일까요?

N은 바로 neighborhood입니다. Lucas-Kanade Method는 아래 그림과 같이 영상을 일정한 크기의 section으로 나눕니다.

그러면 각 섹션의 크기를 \sqrt{n} 라고 했을 때, 각 섹션에는 \sqrt{n} \times \sqrt{n} 개의 픽셀들이 존재합니다.

이 \sqrt{n} \times \sqrt{n} 개의 픽셀들을 통해 u와 v를 구하는 constraint 방정식을 n개 만큼 만들 수 있어서 일단 UnderDetermined 문제를 해결할 수 있게 됩니다.

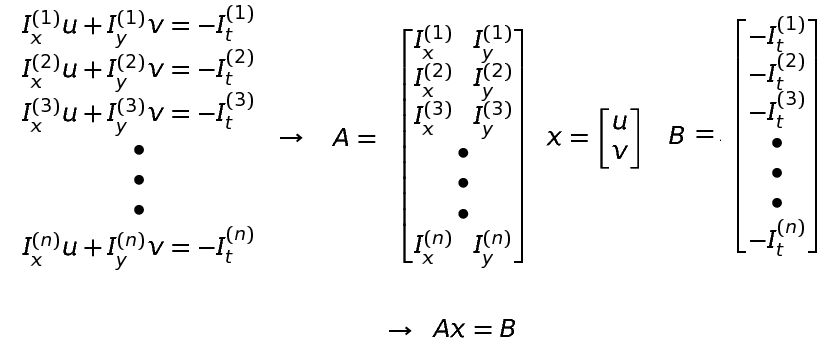
n개의 pixel을 통해 만든 n개의 방정식

자 그럼 UnderDetermined 문제는 해결했지만, 우리가 구하려는 미지수 u, v 보다 더 많은 방정식(n개)이 존재하기에 OverDetermined 상황이 되버렸습니다.

이 OverDetermined인 식인 Ax = B 는 최종적으로 {x = (A^{T}A)^{-1}A^{T}B}로 구할 수 있게 됩니다.

OverDetermined 식을 푸는 방법은 투영변환 행렬을 계산할 때 다뤘으므로 설명하지 않겠습니다.(궁금하신 분은 http://server.rcv.sejong.ac.kr:8080/2020/07/19/multiview-geometryhomogeneoushomography/ 참조)

이러한 Lucas-Kanade 방식은 각 픽셀 별 optical flow를 계산하는 것이 아니라, 각 섹션 별 optical flow를 계산하는 것이기 때문에, 정보가 Dense하지 못하고 부족하다는 단점이 존재합니다.

Variational Method

두 번째 방법론은 Variational Method 입니다. 해당 방법론은 기존 Optical Flow constraint에서 Smoothness Constraint가 추가 된 것입니다.

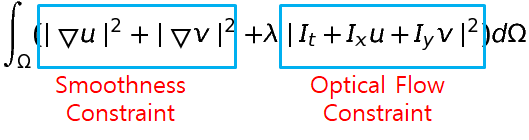
간략하게 설명드리면, 먼저 Lucas-Kanade 방식에서는 일정한 섹션을 나누어 해당 섹션 내에 벡터들은 모두 동일한 방향으로 움직인다는 제약조건을 주었습니다.

Variational Method 역시 인접한 벡터들이 동일한 방향으로 움직이게끔 제약 조건을 주지만, 강제적으로 주는 것이 아닌, Optical flow map에서 수평 방향, 수직 방향으로의 변화량이 크지 않게끔 하는 것입니다.

Smoothness Constraint의 수식을 보시면 아시겠지만, u와 v를 미분한 값을 의미합니다. 여기셔 u와 v는 두 인접한 프레임 사이에 이동 거리 값을 의미하므로, u와 v의 미분 값은 속도라고 볼 수 있습니다.

쉽게말하면 연속적인 프레임에서는 물체의 속도 변화가 급격하게 일어날 수 없으며 인접한 픽셀들끼리는 유사한 크기와 방향으로 이동하는 것을 표현한 것입니다.

이러한 결과를 기반으로 optical flow의 변화량이 크지 않게끔 이를 조정하는 제약 조건을 설정하게 되었고 이는 위에 수식에 Smoothness Constraint(Total Variation Loss)입니다.

Total Variation Loss를 계산하는 방식은 위에 L2 loss 버전과 그림에는 없지만 L1 버전도 있습니다.

Large Displacement

앞에서 설명한 두 방법론들은 공통적으로 Large Displacement에 취약하다는 단점이 존재합니다.

Large Displacement란 어떤 영상 내 물체가 크게 움직여서 다음 프레임 영상과 이전 프레임 사이에 위치 변위량이 커졌을 경우, 이를 optical flow가 잘 반영하지 못하는 것을 의미합니다.

위치 이동량이 매우 큰 경우에 앞에 방법론들이 optical flow vector를 잘 구하지 못하는 이유는, 바로 optical flow 제약식을 구할 때 1차 테일러 급수를 사용했기 때문입니다.

위에서도 설명을 드렸다시피, 테일러 급수의 차수가 커지면 커질수록 기준 지점으로 부터 더 넓은 영역을 근사할 수 있습니다. 하지만 앞에 설명드린 방법론들은 사실상 물체의 움직임이 작다는 전제가 있었기에 1차 테일러 급수를 사용했었습니다.

Coarse-to-Fine Method

이러한 Large Displacement를 해결하고자 여러 방법론들이 또 제안되었는데, 그 중 하나는 바로 Coarse to Fine Method 입니다.

해당 방법론의 컨셉은 매우 간단합니다. 바로 Large Displacement인 영상을 DownSampling하여 Small Displacement로 바꾸자는 것입니다.

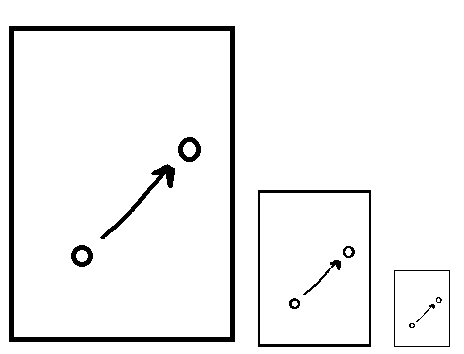
위에 그림과 같이, 원본 크기의 영상에서는 large displacement이지만, 영상을 downsampling할수록 이동 변위량이 작아지는 것을 확인하실 수 있습니다.

이러한 컨셉을 가지고, 먼저 low resolution에서 optical flow vector를 구하고, 이를 점점 high resolution으로 키워나가는 방식을 사용합니다.

하지만 이렇게 resolution을 변경하는 방법은 공통적으로 발생하는 문제가 존재하죠. 바로 sampling하면서 원본 영상 대비 정보량의 손실이 발생한다는 것입니다.

해당 방법론 역시 이러한 문제점이 발생하였고 한계가 뚜렷합니다.

Large Displacement Optical Flow

Large Displacement Optical Flow는 2011에 나온 논문으로 위에서 말한 large displacement를 해결하고자 하는 또 다른 방법론입니다.

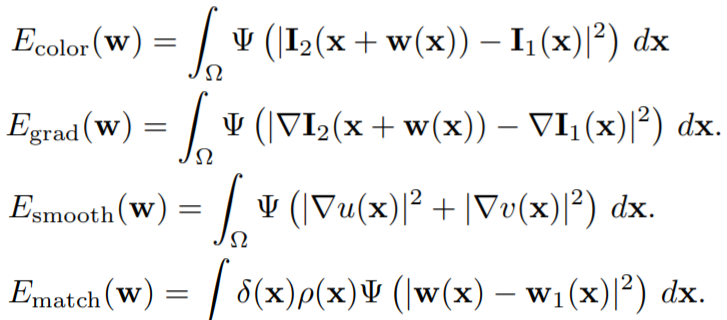
위에 수식들은 해당 논문에서 minimize하려고 하는 loss들을 나열한 것입니다.
수식이 4개인만큼 차근차근하게 설명해볼게요.

먼저 해당 수식 속 변수들의 의미는 아래와 같습니다.

• w(x) – 영상 속 물체가 이동하는 변위값 (u , v)
• \Psi – 해당 논문에서 설계한 함수로 \Psi(s^{2}) = \sqrt{s^{2} + 10^{-6}}을 나타낸다.</li><li>[latex] I_{2}, I_{1} - 각각 다음 프레임 영상과 이전 프레임 영상.
• \delta_{j} - matching point가 존재하는지를 나타내는 flag 값 (0 또는 1)
• \rho - matching score
• g(x) - region boundary map

먼저 첫번째 수식은 우리가 잘 아는 optical flow의 제약값입니다. 근데 자세히 보시면 이전에 방법론들은 모두 1차 테일러 급수를 이용하여 함수 I에 들어있는 u, v(위에 수식에선 w(x)로 표현)를 함수 밖으로 빼내었지만, 해당 논문에서는 그러지 않았습니다.

그 이유는 해당 방법론에서는 robust function(\Psi)을 적용한 후 gradient descent를 하여서 u, v를 구하기 때문입니다. 여기서 robust function을 적용하는 이유는 해당 함수를 적용 시 outlier들을 제거시키는 효과가 있기 때문입니다.

두번째 수식은 영상의 gradient를 뜻하는 제약 조건 입니다. 위에 첫번째 optical flow 제약은 RGB 또는 gray의 영상을 표현하는데, 이러한 영상들은 밝기 변화 등에 이유로 인하여 가끔씩 신뢰하기 어려운 값들을 출력합니다.

즉 첫번째 제약 조건을 보완하기 위해 나온 것이 gradient constraint이며, 해당 수식은 2차 방정식이므로 노이즈에 강하고 불변성들을 지니고 있습니다.

세번째 수식은 위에서 설명한 Smoothness constraint이므로 설명은 생략하겠습니다.

네번째 수식이 해당 논문에서 가장 중요한 핵심입니다. 해당 constraint는 바로 descriptor based feature matching을 뜻합니다. feature descriptor는 keypoint의 특징을 나타내는 값으로 가장 잘 알려진 예시로는 SIFT가 있습니다.

먼저 w(x)는 optical flow vector 값을 의미하며, w_{1}(x) 는 descriptor 기반 feature matching을 통한 결과값입니다.
즉 optical flow vector 값을 feature matching 결과값과 유사하게끔 만들겠다는 것이죠.

Descriptor based Feature Matching의 예시로, 완전히 다른 viewpoint에서 촬영했지만 matching이 되는 것을 확인할 수 있다.

그 이유는 바로 descriptor 기반 매칭 방식이 Large Displacement에 상당히 강하다는 점입니다. descriptor를 이용한 매칭은 연속적인 frame뿐만 아니라, 완전히 다른 view에서 촬영한 사진들 사이에서도 매칭이 될 정도로 상당히 Large Displacement에 강인한데, 이러한 강점을 optical flow vector에게도 적용시키려고 하는 것입니다.

EpicFlow

해당 방법론을 마지막으로 hand-craft 방식의 optical flow 방법론 소개를 마치려고 합니다.

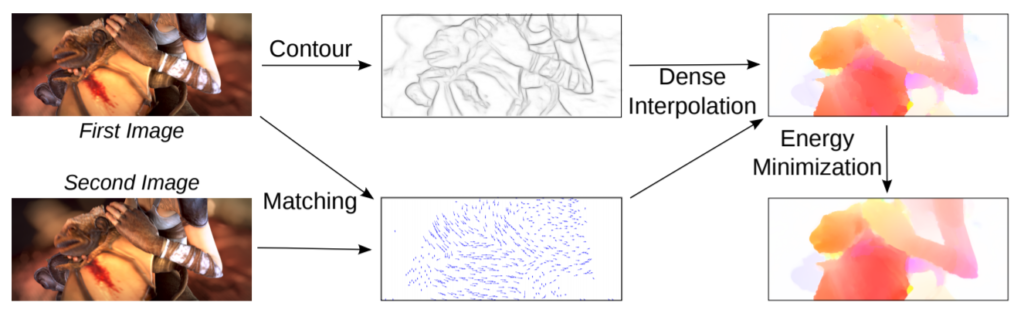
먼저 해당 방법론 역시 feature matching을 추가하여 optical flow map을 구합니다. 하지만 여기서 추가로 첫번째 영상으로부터 edge map을 출력 후 해당 edge map을 사용하여 optical flow map의 edge를 더 샤프하게 만듭니다.

그럼 이 edge map을 어떻게 활용하는지에 대해 알아봅시다.

먼저 EpicFlow도 이전에 방법론들처럼, Coarse-to-Fine method를 사용합니다. 해당 방법론은 위에서도 설명드렸다시피, low resolution에서 점차 high resolution으로 upsampling하는 과정을 거치며 optical flow map을 보완해 나갑니다.

이 때 upsampling을 하기 위한 interpolation을 최근접 보간을 활용하게 된다면, 일반적으로 유클리디안 거리를 통해서 계산을 하게 됩니다. 하지만 이 방식은 optical flow에서 문제를 유발합니다.

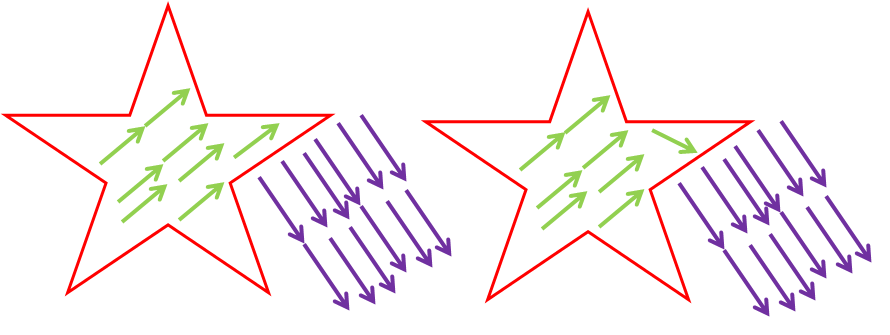
위에 그림을 보시면 좌측과 같이 별 안에 존재하는 픽셀들은 모두 유사한 방향과 크기의 optical flow vector 를 가져야만 합니다. 근데 만약 유클리디안 거리를 통해서 interpolation을 하게 되면, 별의 모서리 부분의 픽셀들은 별 바깥에 픽셀의 vector(보라색 화살표)값으로 매핑될 수가 있습니다.

즉 물체의 외곽에서는 물체 내부의 값들과 외부의 값들 사이에 유클리디안 거리가 비슷하기 때문에, 정확한 optical flow vector를 가지기 힘들며 이로 인하여 외곽에 대한 결과값이 선명하지 않게 됩니다.

이를 해결하고자 해당 논문에서는 물체의 경계선을 기반으로 한 Geodesic distance를 사용합니다. 이 geodesic distance를 사용하기 위해 초기에 edge map을 구한 것 입니다.

Geodesic distance란 쉽게 말해 한 지점에서 다른 지점까지의 이동경로를 나타내는 거리 값입니다. 아래 그림을 보시면 이해가 빠르게 되실 겁니다.

유클리디안 거리는 한 지점에서 다른 지점으로의 직선으로 측정한 길이이므로, 경계선의 유무와는 상관없이 거리를 구합니다. 하지만 geodesic distance를 이용한다면, 경계선을 지날 때 보다 지나지 않은 픽셀이 최단경로인 것으로 계산 가능합니다.

이러한 방법을 통해 외곽에서의 optical flow 정확도를 향상시킬 수 있었습니다.

Coarse-to-Fine과 EpicFlow 정성적 결과 비교

이상으로 hand-craft 기반 optical flow에 대해서 알아보았고, 시간이 되면 deep learning 기반 optical flow에 대해서도 리뷰하고자 합니다.