작성 중
해당 리뷰는 Dive into Deep Learning(https://d2l.ai/index.html)의 6장 Convolutional Neural Networks의 1절 From Fully-Connected Layers to Convolutions의 내용을 가져왔습니다. fcn에서 conv layer로 변경시키며 설명해주는 부분이 인상적이고 이로인한 conv의 필요성과 유용성에 대한 이해가 와닿아, 다른 연구원분들에게 소개하고자 리뷰를 하게 되었습니다.
MLP를 활용하는 데이터들은 대부분 표로 정리된 데이터를 사용합니다. 세상에 존재하는 데이터들은 수치화가 가능하고 각각을 독립적인 구분이 가능한 데이터도 많지만, 영상과 같이 공간적 구조가 증요한 데이터들도 존재합니다.
먼저 1,000개의 히든 스탯을 가진 fully connected layer를 이용하여 1M 픽셀을 가진 개와 고양이 영상을 구별하고자 합니다. fcn을 학습하기 위해서는 10^6 × 10^3 = 10^9이 필요하게 됩니다. 수많은 파라미터로 분류기를 학습해야하고 그에 따라 많은 데이터셋이 필요하게됩니다.
하지만 오늘날 컴퓨터는 사람만큼 개와 고양이를 잘분류하며, 인식 문제에서는 사람을 넘었다는 결과도 있을 정도입니다.
이번 세션에서는 공간적 구조의 정보가 중요한 영상 데이터 인식에서 획기적인 성능을 보이도록 만들어준 convolution neural network에 대해 소개해드리고자 합니다. 저는 fcn layer에서 conv layer로의 변화 과정에 집중해 설명해 드리고자 합니다
이 복잡한 영상에서 사람들은 왈도를 찾아내기 위해서 한 패치씩 차근차근 위에서 아래로 혹은 왼쪽에서 오른쪽으로든 객관성을 위하여 최대한 유사한 방법으로 찾아보려고 합니다. conv는 위의 방법과 유사합니다. 공간적 구조를 유지하며 그럼으로써 파라미터 수를 줄여 파라미터와 유용한 표현력을 기릅니다.
영상 데이터에서 획기전인 성능을 보이도록 만들어준 conv를 fcn에서 변경하기 위해서는 사람이 영상에서 물체를 찾는지 알고 이를 닮도록 만드는 것에서 시작합니다. 예를 들어 돼지는 하늘을 날지 않고 비행기는 수영을 하지 않는 것을 사람들은 알고 있습니다. 하지만 사람들은 하늘을 나는 돼지와 수영하는 비행기 영상 속에서도 돼지와 비행기를 찾아냅니다. 좀 더 설명하기에 매우 좋은 예시가 있습니다. 그림 6.1.1 where’s waldo는 그림 속에서 왈도 캐릭터를 찾아내는 게임입니다. 왈도는 개성있는 복장을 입고 있지만, 수많은 사람과 정신없는 것들로 인해 놀랍게도 왈도를 찾아내기 힘듭니다
이제 나열할 몇가지 지켜야 할 규칙을 지킨다면 컴퓨처 비전에서 유용한 아키텍쳐를 가진 cnn을 만들 수 있습니다.
1. 초기 계층에서는 네트워크가 영상 어느 부분에 나타나든 동일한 패치로 유사하게 작동해야합니다. 이를 translation invariance라고 합니다
2. 네트워크의 초기 계층에서는 영상의 로컬과 먼 거리의 영상 내용과는 관계없이 로컬 지역에 초첨을 맞춰야 합니다. 이를 locality라고 칭하며, 결국 이러한 로컬 표현은 전체 이미지 수준에서 예측을 위해서 집계 되어 사용됩니다.
Constraining the MLP
수식 설명, k는 feature 갯수, l은 feature 길이
,수식 6.1.1은 패치가 적용된 fcn임.
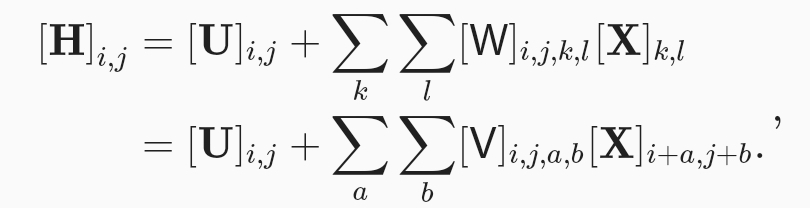
Translation Invariance
수식 6.1.2은 U가 bias라서 상수이기에 u로 단순화, v와 u는 영상 위치와 관계 x(translate invarinace에 기초하여) 수식 단순화
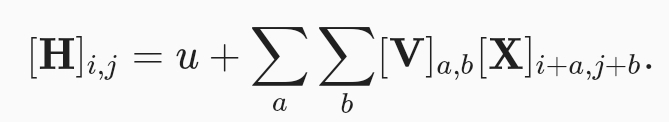
Locality
locality에 기초하여 먼거리에 위치한 영상 정보를 보지 않도록 범위 지정 해줌
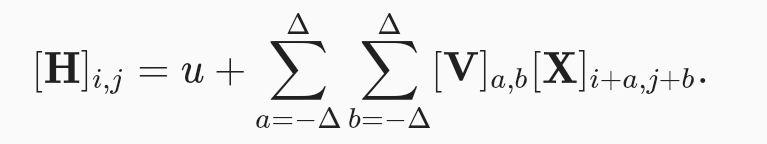
이것이 conv layer이며, ,v가 conv 필터 혹은 커널이라고 부릅니다.
이전 수십억개의 파라미터가 필요했던 fcn은 conv 필터를 이용함으로써 드라마틱하게 파라미터가 줄어들게 됩니다. 또한 공간적인 정보를 활용함으로써 효율적이며 강력한 모델을 만들 수 있게 됩니다.
Convolutions
계속 나아가기전에 왜 conv라고 하는지, 하나의 함수와 또 다른 함수를 반전 이동한 값을 곱한 다음, 구간에 대해 적분하여 새로운 함수를 구하는 수학 연산자이다. i+a는 상광 i-a는 conv 어쩌구
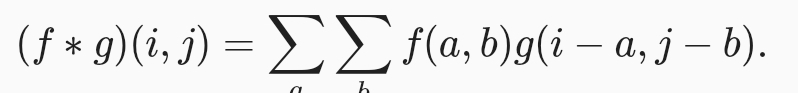
Channels
왈도로 돌아가서, conv레이어는 그림 6.1.2에서 보이늗 것처럼 필처 v의 사이즈와 웨이트의 강도를 결정합니다. 우리의 모델은 왈도니스가 가장 높은 것을 얻도록 배우게 됩니다.

채널. 한가지 문제를 간과하였습니다. 그림 6.1.2 처럼 영상은 그리드 형태의 영상 표현말고도 컬러영상을 표현하기위한 rgb의 3개의 채널로 구성된 점입니다. 실제로 영상들은 2차원 객체가 아닌 높이와 너비 그리규 채널이 특징인 3차원 텐서입니다. 1024 1025 3에서 두축은 공간 관계와 연관 마지막 축은 각 위치의 픽셀에 할당된 다차원 표현으로 볼 수 있습니다. 따라서 X는 삼차원 텐서이뤄집니다. 필터 V 또한 삼차원 텐서로 변경하여 사용합니다.
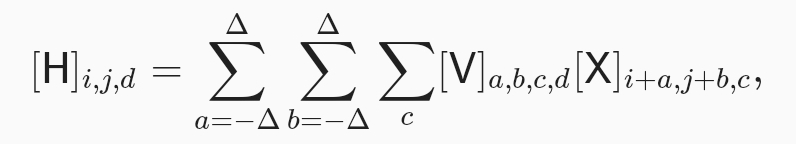
이외에도 해결할 문제는 많습니다. 모든 히든 리프리젠테이션을 어떻게 단일 리프리젠테이션으로 변경할지, 이미지에 왈도가 있는지 파악 여부 방법, 효육적인 연산장법, 레이러를 결합하는 방법, 적절한 활성화 함수 및 실제로 효과덕인 네트워크를 생성하기 위한 합리적인 설계 선택을 하는 방법을 이후 발표로 설명할 예정입니다.
