해당 논문은 연산량과 메모리를 극단적으로 줄여주는 방법 중인 하나인 precision을 Binary로 사용하는 Binary network에 모델의 구조와 하이퍼 파라미터를 학습하여 모델을 만드는 Neural Architectures Search(NAS)를 적용하여 binary network를 찾는 Binary Network Architecture Search(BNAS)를 제안하는 논문입니다.
contribution
BNAS가 기여한 바는 아래와 같습니다.
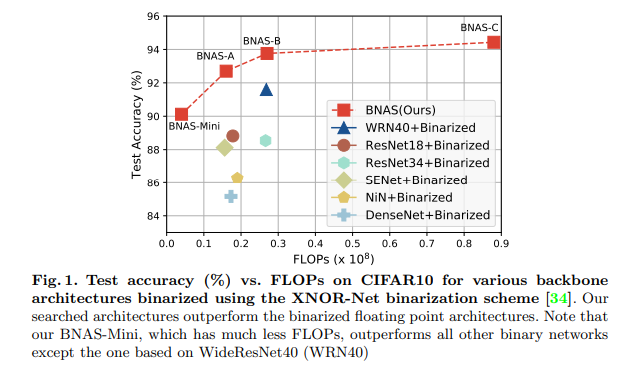
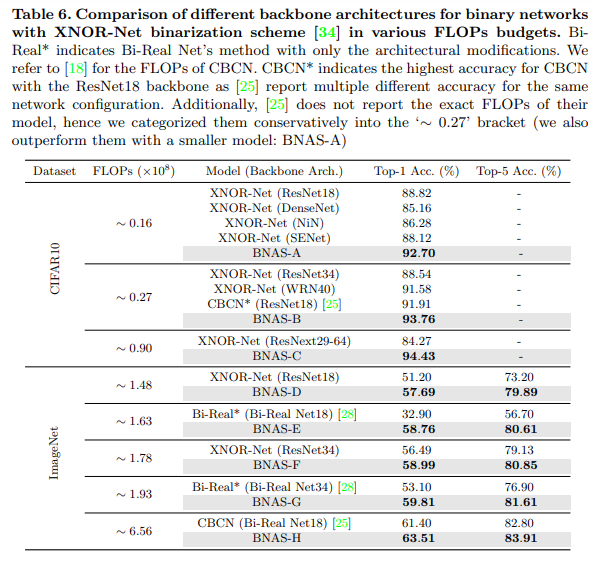
- 첫 번째로 architecture search method for binary network를 제안했습니다. 검색된 아키텍쳐는 FLOP에 따라 조정이 가능하며, NAS에서 많이 비교하는 CIFAR10과 ImageNet에서 SOTA를 달성한 binary network보다 우수한 결과를 냈습니다. (Fig 1. 참고)
- 보다 quantization error에 강인한 새로운 Search Space for binary network 제안했습니다.
- 모델 search의 초기화의 다양화와 좋은 성능을 내는 binary network를 발견하기 위한 새로운 search object를 제안했습니다.
++ search space나 search object는 NAS에서 사용되는 용어로 그에 대한 정의는 아래와 같습니다.
search space : NAS에서 모델을 구성하기 layer, 혹은 하이퍼 파라미터 값을 담은 template를 기준으로 최적의 모델을 찾아야하는 공간.
search object : search space에서 최적의 모델을 찾기 위한 지표, e.g. 정확도, loss 등
Related Work
Binary Neural Networks
작성 예정 – x-review로 링킹할 예정
Neural Architecture Search
작성 예정 – x-review로 링킹할 예정
Binarizing Searched Architectures by NAS

NAS가 CIFAR10과 ImageNet에서 압도적인 성능으로 보여 좋은 방법론이라는 것은 자명한 사실입니다. 그렇기에 보다 좋은 binary network를 얻기 위해서 cell based gradient search methods 방법을 가진 NAS인 GDAS, DARTS, SNAS에 binary network로 유명한 XNOR-Net을 적용하여 시험을 했습니다.(Fig 2.) 실험 결과, 기존 floating point를 사용하는 NAS 방법들은 학습이 안되거나, 진행되면서 성능이 급격하게 안좋아지는 결과를 보였습니다. 이에 대해 저자들은 2가지 이유를 제시했습니다.
1) 기존 floating point NAS들의 Search space는 binary network에 맞지 않아 quantization error가 커진다. (e.g separable convolution, 아래 세션 참고.)
2) quantization error가 너무 커져 cell template에 gradient가 제대로 전파 되지 않는다.
그렇기에 binary network에서 최적의 모델을 찾아내기 위해서는 search space와 cell template이 quantization error에도 강력하게 설계되어야 합니다.
Approach
우선 BNAS는 binary network를 검색하기 위해서, cell-based architecture search 방법을 기초하여 사용 했습니다. 아래의 수식은 cell-based 방법를 일반화 한 식입니다.
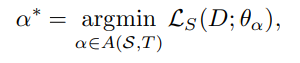
- A : 실현 가능한 최종 모델의 집합
- S : Search space (layer type)
- T : cell template (선택된 layer type에서의 사용됨)
- D : Dataset
- L_s : search objective
- theta : 선택된 아키텍쳐의 파라미터
- alpha : 선택된 아키텍쳐
cell-based architecture search은 eq 1.을 통해 L_s : search objective이 가장 작은 최적의 모델을 찾아냅니다. precision을 binary로 변경하기 위해서 아래의 수식으로 변경합니다.
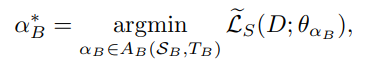
- S_B : new search space (binary) – binary weights, activations
- T_B : new cell template (binary) – more robust to quantization error
- ~_L_s : new search objective (binary) – diverse search
BNAS는 기존의 floating point의 값들에서 quantization error에 보다 강인함을 고려하여 binary로 변경된 S_B, T_B, ~_L_s의 구성으로 상단 세션에서 제시한 2가지 이슈를 해결합니다.
Search Space for Binary Networks (S_B)
BNAS는 기본적으로 유명한 floating point NAS를 이용하여 설계되어지고, quantization error를 줄이기위해서 Xnor-Net의 binary scheme을 사용합니다.
- Convolutions and Dilated Convolutions
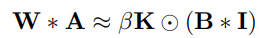
- W : floating point Conv layer의 weight
- A : input activation
- B : binary parameter = sign(W)
- I : binary input activation = sign(I)
- beta : 1/n ||W||
- K : D * k, D = sigma(A, : , :)/c , k_i,j = 1/(w,h)
- Hadamard product : element wise multiplication, 매트릭스간 요소 곱
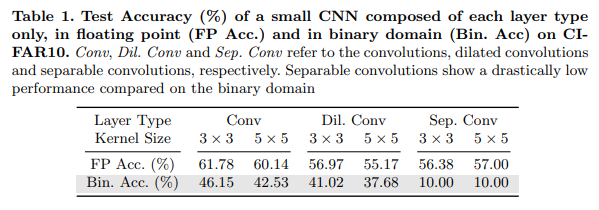
Table 1.을 보면 quantization error로 인해서 binary conv/Dil Conv의 성능적 한계가 존재하는 것을 볼 수 있다. 그렇기에 BNAS에서는 Xnor-net에서 제안한 scheme와 다르게 standard conv/Dil Conv를 search space에 포함합니다.
2. Separable Convolutions
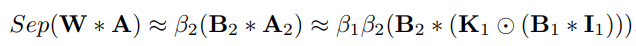
Separable Convolutions는 CNN계열에서 파라미터의 갯수를 줄여 계산 복잡도를 줄이는 방법으로 많이 사용되어집니다. 하지만 BNAS에서 주장하길 Separable Convolutions를 이진화를 한다면 eq 4의 수식을 가지며 이진화된 weight와 activation의 한계를 보완하는 scale factor(beta_1, beat_2, K_1) 갯수가 중첩된 conv로 인해 늘어나게 되면서 quantization error가 늘어나는 현상이 생깁니다. 그로인해 table 1.에서도 볼 수 있듯이 binary Separable Convolutions의 정확도가 random sampling한 결과와 동등한 결과를 볼 수 있습니다.(table 1.은 CIFAR10에서 실험한 결과) 이런 결과는 fig 2.에서 많은 수의 Separable Convolutions을 선택하는 DART가 이진화될 경우 학습이 되지 않는 이유에 대한 설명이 됩니다. 이러한 실험적 결과로 BNAS는 Xnor-Net과 다르게 Separable Convolutions을 Search space에 포함하지 않습니다.
3. Zeroise.
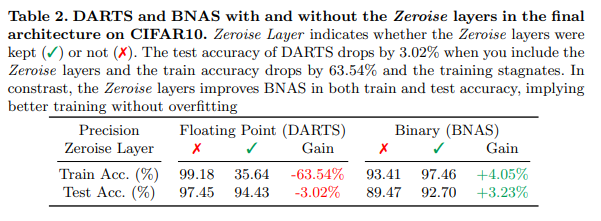
DARTS에서 제안된 Zeroise layer는 입력에 관계없이 포함된 모든 0을 출력합니다. 이는 모델의 연결 부족을 표현하기위해 설계된 layer입니다. 만약에 zeroise layer가 선택된다면, 두번째로 좋은 layer로 대체 합니다. 또는 모든 layer가 zeroise layer로 대체됨으로써 node(cell)간의 연결을 끊는 역할을 합니다. BNAS에서는 더 나아가 zeroise layer를 끊는 역할이 아닌 binary의 sign을 표현하는 하나의 layer로써 사용(topology)합니다. table 2.를 보면 zeorise layer의 유무의 영향이 오버피팅을 방지하며 성능을 향상 시키는 모습을 볼 수 있습니다.
결론적으로 BNAS의 search space는 table 3.과 같습니다.

Cell Template for Binary Networks (T_B)
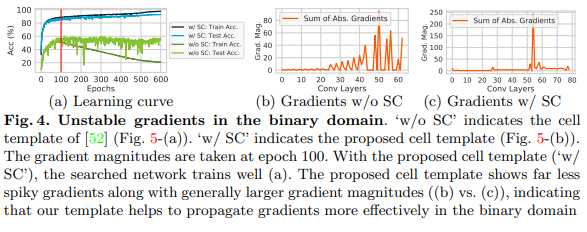
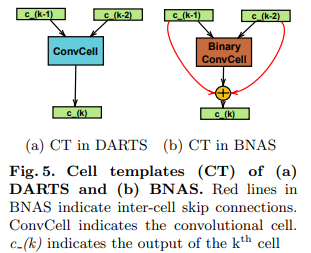
Fig 4에서의 결과와 같이 NAS에서 제안된 cell template를 사용하면 gradient가 제대로 propagation 되지 않는 문제점이 있다. quantization error를 항상 출력하는 문제를 발생시킵니다. BNAS에서는 이를 해결하기 위해서 누적된 에러 없이 정보를 전달할 수 있도록 skip connection을 사용할 것을 제안합니다. 특징적인 부분은 back-propagation이 되지 않도록 intra-cell skip-connections를 사용합니다. (fig 5. skip-connections을 사용한 cell template)
Search Objective with Diversity Regularizer ( ~_L_s )
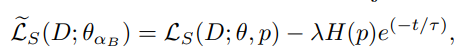
- 기본적으로 eq 2.와 동일한 파라미터를 사용합니다.
- 해당 수식은 DARTS를 기반으로 만들어졌습니다.
- DARTS는 두번의 update로 학습을 합니다. 모델의 구조를 결정하는 theta와 파라미터, layer의 종속성을 결정하는 p로 나눠져 학습이 이뤄집니다.
- eq 5. cross-entropy loss와 닮은 형태를 가집니다.
- t : epoch
- lambda : balancing hyper-parameter
- H : entrophy
- eq 5. 수식은 초기에 다양한 layer를 변경하며 볼 수 있도록 장려할 수 있도록 설계되어집니다.
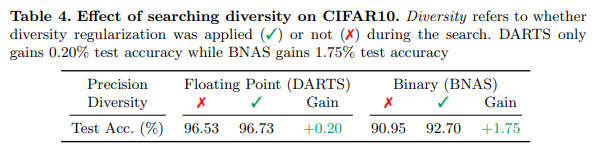
Experiments
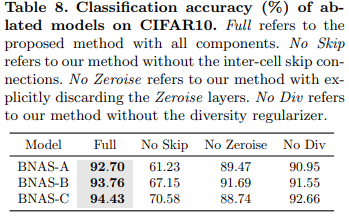
Ablation Studies