해당 논문은 CVPR2018 논문으로 고려대학교 김창수 교수님 연구실에서 나온 논문이다. 해당 논문은 하나의 이미지로 Depth를 Estimation 하는데 있어 small ratio yield에서의 depth estimation은 details 잘 살아있고, large ratio에서는 전반 적인 depth distribution이 잘 나타난다는 점에서 원본 이미지를 랜덤하게 crop하여 여러개의 small ratio 이미지로 만든 후에 depth estimation을 수행하고 결과를 Fourier domain에서 결합하는 방법을 제안하고 있다.
- Depth Estimation Network

본 논문에서는 Depth Estimation 을 위해 ResNet-152을 변경해 네트워크를 구성하였다. 해당 모델은 최종적으로 Depth map을 예측한다. 위의 그림에서 파란색은 기존 ResNet-152에서 사용되는 구조로, 각 블럭들은 아래 그림에서 파란색 점선 영역의 네트워크로 구성된다. 그리고 초록색은 해당 논문에서 제안한 수정된 ResNet 블럭이며, 해당 레이어에서의 feature map을 추출하기 위해서 변경된 구조이다.
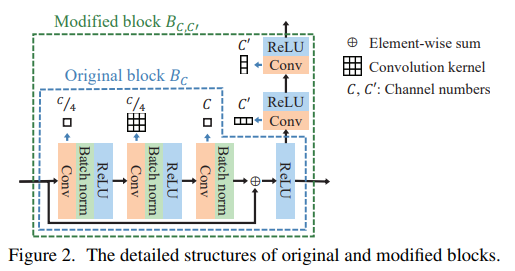
해당 네트워크는 2 stage 방식으로 학습이 되며, 처음에는 Original block만 가지고 학습을 수행한다. 이때는 ResNet-152 구조와 같기 때문에 기존 ResNet-152을 학습하는 방법과 같으며, classification을 위해서 학습된 pretrained 체크포인트를 가져와 depthmap을 GT로 학습시킨다. 충분히 학습이 된 이후에는 feature extractor를 위해 Modified block 부분을 추가하여서 (이때 모든 부분을 추가하는게 아니라 마지막 19개 block에만 Modified block으로 변경한다.) 한번더 학습을 수행한다. 이때 파라미터는 Gaussian random values로 초기화 한다. 이를 통해서 모델이 더 빠르게 학습을 수행하고 더 정확한 Depth Estimation이 가능하도록 하였다고 저자는 말한다.
2. Depth-Balanced Euclidean Loss
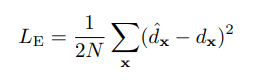
다음으로는 Loss를 설명하는데, 일반적으로 Regression 문제에서는 위의 수식과 같이 Euclidean loss를 종종 사용한다. 하지만 위의 loss를 Depth Estimation에 그대로 사용할 경우 한가지 큰 문제가 존재하는데, far object에 대해서 loss가 민감하게 반응한다는 것이다. 풀어서 설명하면 far object와 near object를 비교하면 같은 3%의 오차범위를 갖는다고 하더라도 near object 의 오차범위보다 far object에서의 오차범위의 크기가 크기 때문에 far object가 네트워크 학습에 더 큰 영향을 미친다. 따라서 이러한 부분을 해결하기 위해서 해당 논문에서는 depth-balanced Euclidean(DBE) loss를 제안하며 수식은 아래와 같다.
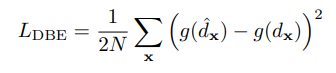
여기서 g는 quadratic function으로 앞서 언급한 far object 와 near object와 밸런싱을 맞추는 역할을 수행한다. 해당 함수의 수식은 아래와 같다.
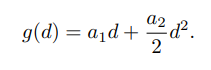
DBE loss를 통해서 backward를 시키는 과정을 좀더 디테일하게 살펴보면 해당 loss가 weight를 업데이트 하는 것을 편미분으로 표현하면 다음과 같다. 여기서 a1은 상대적인 크기를 나타내는 수, a2는 음수로 설정한다.(추후 보충설명 예정)
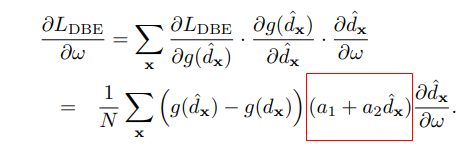
실제 weight가 업데이트 되는 과정에서 분석하면, 앞선 loss function의 설계로 large depth의 경우 bigger error의 영향이 위 수식에서 빨간색 부분에 의해서 감소하는 것을 알 수 있다.
3. Depth Map Candidate Generation
아래 그림과 같이 앞서 언급한 저자가 제안하고 있는 네트워크는 DBE Loss를 사용해 입력된 이미지에 대한 depth map을 생성한다.

일단 가장 먼저 언급했던 했지만, 해당 네트워크는 원본 RGB이미지를 여러 ratio로 crop한 후에 해당 이미지에 대한 depth map을 구하고 마지막에 이를 Fourier Domain에서 합친다. 위의 그림에서 (b)~(e)에는 crop할때의 ratio를 우측 상단에 표현하였다. 각 crop image들의 depth map을 구한 후에는 결합을 해야하는데, 이때 각 crop된 이미지들에 scale factor인 1/r를 곱한 다음에 합친다. 이때 scale facotr가 곱해지는 이유는 ratio로 crop한 이미지는 해당 ratio의 역수만큼 zoom이 된것 같은 효과를 나타내기 때문이다.
4. Candidate Combination in Fourier Domain
자 거의 다왔다. 이제 위에서 구한 Candidate Depth map들을 결합(merge, Combination) 해야한다. 이때, 논문의 핵심 contribution 중 하나인 Fourier Domain에서의 결합이 사용된다. 일단 해당 Depth map을 discrete Fourier transform(DFT)를 통해서 Fourier Domain의 DFT vector로 변경한다. 이때 수식은 아래와 같다.
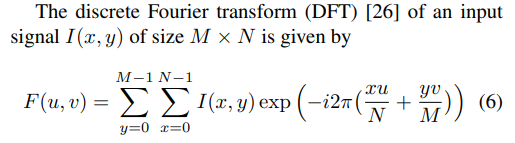
(2D-DFT에 대해서는 지난학기 영상처리를 연구원들이 모두 열심히 들었다고 생각하므로 자세히 설명하지 않는다.)
모든 candidates depth map을 DFT vector로 변환한 다음 해당 vector를 다음과 같이 결합한다. 아래 수식에서 m은 m번째 depth map, w는 weight, b는 bias이다.
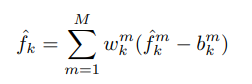
이때 bais는 training 데이터를 가지고 사전에 구하는데 그 수식은 다음과 같다.
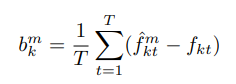
weight는 f_k 와 predict f_k의 MSE를 최소화하기 위한 파라미터인데, 이도 아래 수식으로 결정한다.

Experimental Results
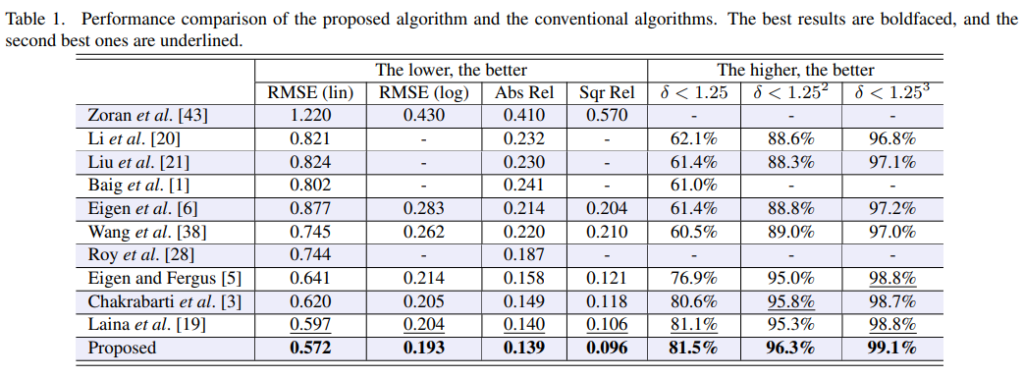
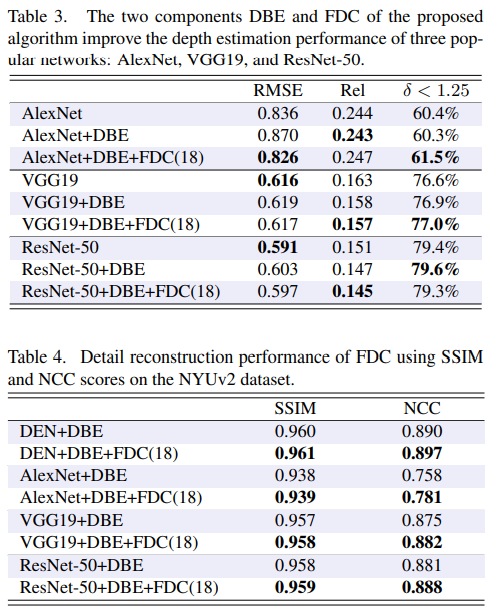

Review
해당 방법론을 2.5D에 적용할 수 있을것 같다. 가장먼저 Loss를 적용해도 될것 같고 공개된 코드를 이용해서 추가적인 Depth map을 예측할 수도 있을것 같다.
리뷰 잘 보았습니다.
전체적인 흐름이 영상을 여러개로 나누어 Depth Map을 구한 후 합치는 부분에도 Contribution이 들어간거 같은데, 맞나요?
그 Depth-Balanced Euclidean Loss 에서 Far object 와 near object를 나누는 기준 같은게 있을까요..? 그리고 그 두개는 GT를 기준으로 Error를 줄이는 게 맞나요..?
네 퓨리에 도메인에서 영상처리때 배운것처럼 퓨리에 도메인의 주파수로 이미지들을 합치는게 Contribution 입니다. 그리고 far object 와 near object는 따로 나누는게 아니라 상대적인 a의 값을 통해서 줄이게 됩니다. 그러면 a에 의해서 상대적으로 depth가 큰 object의 loss와 dpeth가 작은 object의 loss의 밸런스를 맞출 수 있는것 입니다.
ResNet 152 를 태워 나온 25×32 의 피처맵을 gt depth 맵과 비교하여 depth regression을 하는 것 같은데 gt depth 맵이 애초에 25×32 크기로 제공되나요? 아니면 다운샘플링해서 사용하나요? 만약 다운샘플링한다면 원래 해상도에 따라 꽤나 많은 정보가 손실되어 depth regression에서 최대의 성능을 얻어내지 못할 것 같은데 이러한 문제는 어떻게 해결했는지 알려주실 수 있을까요?
저도 해당부분에 대해서 의문이였지만 따로 논문에서 이야기하지 않는것으로 보아 related work중에서 이미 사용한 방법이지 않을까 생각이 됩니다. 공개된 공식 코드에서는 resize를 통해서 GT depthmap을 만들고 있습니다. 아래 코드는 실제 해당 부분을 가져온 부분입니다.
depth = transform.resize(depth, (25, 32), mode=’reflect’,
anti_aliasing=True, preserve_range=True).astype(‘float32’)
depth = np.ravel(depth)
depth = from_numpy(depth)