최근에 object detection 공부를 주로 하고 있어서 해당 주제에 논문을 찾아보던 중에 간단하면서 흥미로운 논문을 발견하여 리뷰하게 되었습니다.
Introduction
다양한 Object Detection task에서 Bounding Box Regression은 매우 중요합니다. 보다 좋은 Regression을 하기 위해 더 좋은 backbone을 사용한다던지, 아니면 더 신뢰성있는 local feature를 추출하는 등 다양한 방법론들이 제안되고 있습니다.
하지만 해당 논문에서는 보다 좋은 regression을 위하여 regression loss 함수를 L1, L2 norm이 아닌, IoU를 통해 바로 계산하자고 제안합니다.
IoU란 아시다시피 Intersection over Union의 약자로, Object Detection에서 성능을 평가할 때 가장 많이 사용되는 평가 metric입니다.
![Tutorials of Object Detection using Deep Learning [4] How to ...](https://hoya012.github.io/assets/img/object_detection_fourth/fig1.PNG)
위에 그림은 IoU를 나타낸 것으로 단순히 두 영역의 교집합을 두 영역의 합집합으로 나눈 것으로 볼 수 있습니다. 이러한 IoU를 구하는 방법 덕분에, 영역의 scale과는 상관없이 항상 0~1사이에 값이 나오는 scale invariance를 보를 나타낸 것으로 단순히 두 영역의 교집합을 두 영역의 합집합으로 나눈 것으로 볼 수 있습니다. 이러한 IoU를 구하는 방법 덕분에, 영역의 scale과는 상관없이 항상 0~1사이에 값이 나오는 scale invariance를 보여줍니다.
일반적인 Object Detection에서, IoU는 단순히 평가를 위한 metric으로 사용됩니다. 예를들어 PASCAL VOC challenge에서는 평가 측정 방식으로 IoU의 임계치를 0.5로 놓습니다.
SSD같은 경우에는 해당 임계치를 넘은 predicted box는 postive, 그렇지 못한 box들은 negative로 분류되어 postive box에 대해서만 loc loss를 L1 norm을 통하여 regression하곤 합니다. 하지만 이러한 대수적인 선택(임의로 특정 임계치를 설정하는 방식)과 L1, L2 norm loss function은 Bounding Box의 Localization을 regression하는데 한계가 존재합니다.
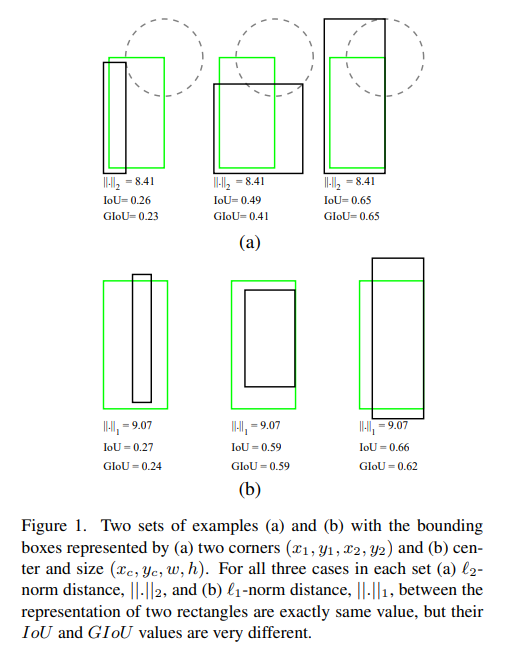
위에 그림을 보시면, (a)는 GT Box와 Predicted Box의 right top 사이의 L2-norm을 나타낸 것이고, (b)는 L1-norm으로 표현한 것입니다.
(a)와 (b)에서 세 유형의 예시가 나와있는데, 해당 예시들 모두 동일한 norm-distance를 가지고 있지만, IoU가 서로 다른 것을 확인하실 수 있습니다.
이게 바로 논문에서 말하는 norm-distance 방식의 문제점인데, 우리가 원하는 것은 predicted box가 gt box와 거의 동일하게 맞추어지기를 원하지만(IoU가 1이 되는 것), 일정 threshold를 넘긴 predicted box를 norm-distance 방식의 loss로 regression하게 되면, 결국 더 좋은 IoU를 가지는 predicted box를 만들지 못하는 경우가 발생합니다.
즉 논문에서는 IoU가 더 큰 box들은 더 작은 loss를, IoU가 작은 애들은 더 큰 loss를 가지게끔 하여 학습을 진행하게끔 하고 싶었고 이를 위해서 norm-distance 방식의 loss 함수를 사용하는 것이 아닌, IoU 그 자체를 가지고 loss 함수를 사용하고자 합니다.
IoU loss의 문제점
하지만 이러한 IoU loss를 곧바로 적용시키기에는 문제가 하나 존재합니다. 예를 들어 두 물체가 전혀 겹치지 않는 경우에, IoU의 값은 0이 되버립니다.(교집합이 0이기 때문) 즉, gradient가 0이 되버리기 때문에, 더이상 optimizing을 할 수가 없게 됩니다.
또한 두번째 문제로는, 마찬가지로 두 object의 영역 교집합이 0일때, 두 object 거리가 멀리 있는지 가까이 있는지에 대한 loss의 차이를 전혀 반영하지 못하게 됩니다. 두 object가 겹치지는 않더라도, 가까이 존재한다면 loss를 작게, 멀리 있으면 loss를 더 크게 반영해주고 싶은데, 애초에 겹치는 부분이 없어 IoU값이 0이 되버리니깐 그러지를 못하기 때문입니다.
이러한 문제를 해결하기 위해 논문에서는 IoU의 특성(장점)은 유지한체 위와 같은 문제를 보완한 새로운 IoU인 Generalized Intersect of Union(GIoU)를 제안합니다.
GIoU
GIoU는 컨셉이 매우 간단합니다. 기존 IoU를 구하기 위한 두 object 영역이 존재한다면, 그 두 object 영역을 감싸는 새로운 영역을 하나 더 추가하는 것입니다.
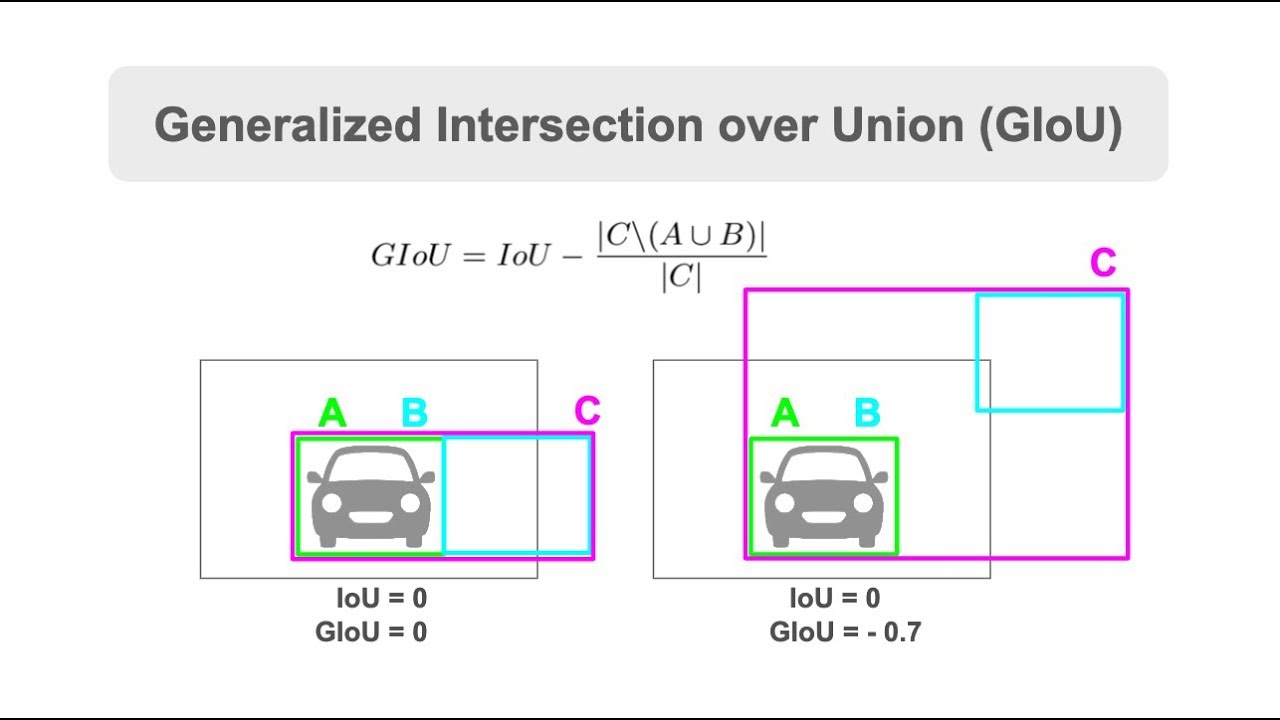
위에 그림을 보면, 기존 IoU에 경우에는 박스 A와 박스 B사이의 합집합, 교집합의 관계를 나타냈다면, GIoU에서는 두 박스를 포함하는 새로운 박스 C가 존재합니다.
그래서 A와 B가 서로 겹치지않는 상황에서 두 박스 사이의 거리가 멀어질수록 GIoU의 값이 달라지는 것을 확인하실 수 있습니다.
그렇다면 GIoU는 어떻게 계산할까요? GIoU를 구하는 방식은 아래와 같습니다.

step1은 좌표 값들이 올바른 크기 순서를 가지는지를 나타내는 condition이고 step2~3은 각 박스들의 영역을 구하는 단계이며, step4은 두 영역의 교집합을 구하는 방식입니다.
step 1~4는 일반적인 IoU를 구하는 알고리즘이라고 보시면 되고, step5~6이 GIoU를 구하기 위한 새로운 영역 C를 구하는 단계인데, 단순히 step 5에서 두 box들 중에서 min max를 통하여 영역 C의 두 대각 좌표를 구한 후 이를 가지고 영역의 넓이를 계산한 것 입니다.
이를 통하여 영역 A,B,C의 넓이를 다 구하였다면, 이제 IoU를 계산할 수 있고, GIoU도 step8에 나와있는 식을 통하여 계산할 수 있게 됩니다. 그리고 GIoU를 통한 Loss는 step9와 같이 1-GIoU값을 통하여 계산할 수 있게 됩니다.
GIoU Loss
GIoU는 일단 IoU와 같이 scale invariance을 가지고 있습니다. 또한 A,B 두 영역을 커버하는 영역 C는 항상 A와 B영역의 합집합 보다 크기 때문에 \frac{A^{c} - \cup }{A^{c}} ( \cup\;is\;union\;of\;A\;and\;B) 는 0과 1사이의 양수값을 가지게 됩니다. 또한 IoU값은 0~1사이의 값을 가지기 때문에 결과적으로 GIoU값은 -1과 1사이의 값을 가지게 됩니다.
그리고 이때 GIoU Loss는 1-GIoU이므로, GIoU Loss의 영역은
0\;\leq\;L_{GIoU}\;\leq\;2 사이의 값만을 가지게 됩니다.
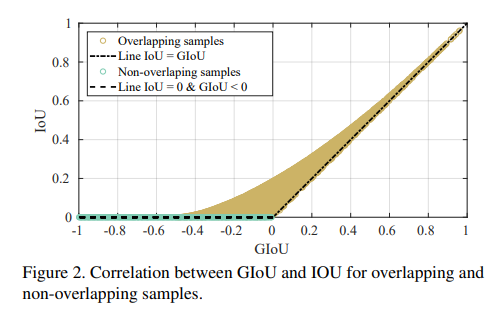
위에 그림을 보시면 IoU에 경우에는 더이상 Overlap하지 않는 구간에서 항상 0에 값을 가지지만, GIoU는 Overlap하지 않는 구간에서도 0이 아닌 값을 가지는 것을 확인하실 수 있습니다.
GIoU loss에 대해서 보다 자세하게 살펴보면, L_{GIoU} = 1 - GIoU = 1 + \frac{A^{c} - \cup }{A^{c}} - IoU 로 나타낼 수 있으며, 만약 두 영역이 서로 겹치지 않아, IoU가 0이라고 가정할 때, GIoU Loss는 간략하게 다음과 같이 표현 가능합니다.

즉 GIoU loss는 gt와 predicted 박스의 합집합은 최대한 크게 하면서, 두 박스를 커버하는 영역 C의 넓이는 최소화하는 방향으로 regression이 진행됩니다.
요약하자면 앞서 언급한 두 영역의 교집합이 0이 되어 IoU가 0이 되었어도, GIoU방식을 통하여 0이 아닌 값이 나오게 되었으며, 두 영역의 거리에 따른 loss의 크기를 반영해줄 수 있게 되었습니다.
Experimental Results
그렇다면 GIoU Loss를 가지고 학습하면 얼마나 큰 성능 향상이 존재할까요?
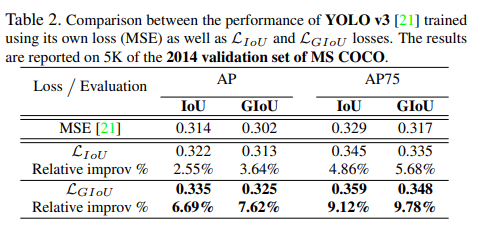
위에 표는 YoLo v3에 대하여 기존 MSE 방식과 IoU loss, GIoU loss를 통하여 학습 및 평가한 결과입니다. 보시면 기존 대비 IoU loss도 약간의 성능향상이 존재하였지만 GIoU는 상대적으로 큰 폭에 성능 향상을 확인하실 수 있습니다.
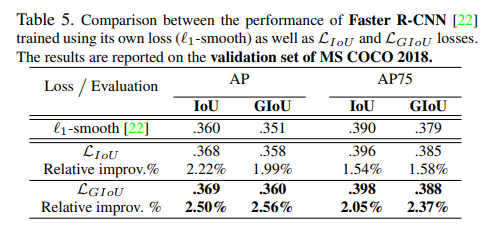
위에 표는 Faster R-CNN에 대하여 MSE, IoU Loss, GIoU Loss 성능을 분석한 표인데, YoLo v3보다는 덜하지만, 그래도 약간의 성능향상을 보여주고 있습니다.
Faster R-CNN에서 YoLo v3와 달리 큰 폭의 성능향상을 보이지 못하는 모습을 논문에서는, Faster R-CNN에 경우 proposal이 YoLo v3보다 dense하게 분포되어 있어 GIoU의 장점인 non-overlapping bounding box에 case가 적기 때문이라고 말합니다.
마지막으로 MSE, IoU Loss, GIoU loss에 대한 정성적인 결과를 보여드리고 글을 마무리 짓겠습니다.


결국 해당 논문은 IoU가 없는 box들은 다 같은 Negative로 설정하였는데, 이러한 방식을 통해서 IoU가 0 이하인 Negative 박스라도 GIoU를 통해서 Negative의 정도를 추가적으로 표현함으로써 성능을 높인다는게 맞나요?
넵
간략하게 요약하면 IoU를 평가로만 쓰지말고, objective function으로 사용하면 성능이 더 좋게 나오는데, IoU Loss에는 overlap하는 부분이 없을 때 단순히 0이 되어 gradient가 최적화되지 못하게 됩니다.
이를 해결하고자 기존 IoU가 비록 0일지라도, gt box와 가까있는 predicted box랑, 멀리있는 predicted box에 대하여 Loss에 대한 차별점을 줌으로써 IoU loss에 대한 단점을 보완하고 장점을 챙겨 성능을 향상시켰다고 보시면 될 것 같습니다.
IOU에 대하여 거리 뿐만 아니라 가로 세로, 또한 물체의 가로 세로비를 이용하여 가중치를 주었다고 이해해도 될까요?
예를 들어 가로 세로 6, 1인 물체의 가로로 a 오차 -> C 박스의 크기 6+a
가로 세로 6, 1인 물체의 세로로 a 오차 -> C 박스의 크기 6+6a
오차의 크기가 같을 때 비율이 더 긴 방향으로의 오차의 가중치가 작음
음 질문하신 예시에 대해서 이해를 제대로 못해가지고, 예시에 대한 답변을 드리기가 어려울 것 같습니다.
가로 세로비를 이용한다는 것에 대해서는 의미를 잘 파악하지 못하였는데
제가 이해한 바로는 gt box와 predicted box가 서로 overlap하지 않은 상황에 대해서 해결방법을 찾고자,
gt box와 predicted box에 대하여 min max 함수를 통해 좌표를 구한 후, 이 두 영역을 모두 커버하는 최소한의 새로운 박스(댓글에서 말씀하시는 C박스)를 도입했습니다.
이를 통하여 C박스의 넓이가 줄어드는 방향으로 학습이 진행되면 IoU가 0인 상황에서도 gradient가 최적화될 수 있는게 이 논문에 핵심 같습니다.
아직 낯선용어가 너무 많은탓에 이해하는데 꽤오랜 시간이걸렸지만, 자세하게 적어주신 덕분에 많은 도움이 됐습니다. 나중에 읽으실 분들에게 있어서 제가 읽을때 헷갈렸던 부분을 적어두려고합니다.
본문에서 아래에 해당하는 내용이 이해가 되지 않았습니다.
” Faster R-CNN에서 YoLo v3와 달리 큰 폭의 성능향상을 보이지 못하는 모습을 논문에서는, Faster R-CNN에 경우 proposal이 YoLo v3보다 dense하게 분포되어 있어 GIoU의 장점인 non-overlapping bounding box에 case가 적기 때문이라고 말합니다.”
따라서, 원문을 찾아보니 아래와 같은내용이 있었습니다.
“First, the detection anchor boxes on Faster R-CNN [22] and Mask R-CNN [6] are more dense than YOLO v3 [21], resulting in less frequent scenarios where LGIoU has an advantage over LIoU such”
as non-overlapping bounding boxes.
본문에 작성하신 proposal이란게 anchor boxes 개수를 의미한단걸 파악하고나서 이해가 갔습니다. 차후에 읽으실 분에게 도움이 됐으면 좋겠습니다.
아직 낯선용어가 너무 많은탓에 이해하는데 꽤나 어려움이 있었지만, 자세하게 적어주신 덕분에 많은 도움이 됐습니다. 나중에 읽으실 분들에게 있어서 제가 읽을 때 헷갈렸던 부분을 적어두려고합니다.
본문에서 아래에 해당하는 내용이 이해가 되지 않았습니다.
” Faster R-CNN에서 YoLo v3와 달리 큰 폭의 성능향상을 보이지 못하는 모습을 논문에서는, Faster R-CNN에 경우 proposal이 YoLo v3보다 dense하게 분포되어 있어 GIoU의 장점인 non-overlapping bounding box에 case가 적기 때문이라고 말합니다.”
따라서, 원문을 찾아보니 아래와 같은 내용이 있었습니다.
“First, the detection anchor boxes on Faster R-CNN [22] and Mask R-CNN [6] are more dense than YOLO v3 [21], resulting in less frequent scenarios where LGIoU has an advantage over LIoU such”
as non-overlapping bounding boxes.
본문에 작성하신 proposal이란게 anchor boxes 개수를 의미한단걸 파악하고나서 이해가 갔습니다. 차후에 읽으실 분에게 도움이 됐으면 좋겠습니다.