Zhengyou Zhang
Basic Equations
Single plane(calibration board가 있는 plane)을 찍어 획득한 영상들을 이용하여 intrinsic parameters 에 Basic constraints 를 부가한다!
Notation


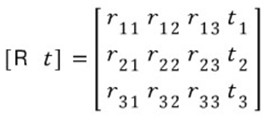
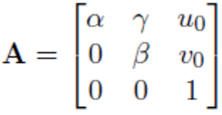
Homography
캘판이 놓인 곳을 Z=0인 지점으로 설정(without loss of generality)


Estimation of the Homography Between the Model Plane and its Image
여기서는 homography 추정을 위해 a technique based on maximum likelihood criterion을 사용하였다.


위의 목적함수를 풀기 위해 nonlinear minimization을 수행하여야 하고, 이 논문에서는 Levenberg-Marquardt Algorithm(LMA)를 사용하여 solution(H)을 획득하였다.
먼저 gradient descent 방법은 그레디언트의 반대방향으로 이동하되 그레디언트의 크기에 비례한 step size 만큼씩 이동하면서 해를 찾아가는 방법이다.
가우스-뉴턴법은 함수의 그레디언트와 곡률(curvature)을 같이 고려하면서 해를 찾아가는 따라서, 가우스-뉴턴법은 gradient descent 방법보다 훨씬 정확하고 빠르게 해를 찾을 수 있다는 장점을 갖는다.
Levenberg 방법은 가우스-뉴턴법을 개선하여 JrTJr에 항등행렬(identity matrix)의 상수배 μI를 더함으로써 발산의 위험성을 낮추고 보다 안정적으로 해를 찾을 수 있도록 한 방법이다
Levenberg-Marquardt 방법은 가우스-뉴턴법의 singular 문제를 피하면서도 μ가 큰 경우에도 곡률(curvature)을 반영하여 효과적으로 해를 찾을 수 있도록 한 방법이다.