[NIPS 2017]Dynamic Routing Between Capsules

Introduction

우리가 잘 아는 CNN은 특징을 검출하는 법을 학습하여 이를 통해 나오는 feature를 해석하는 네트워크입니다. 이는 영상 각각의 위치를 돌아다니면서 좋은 가중치 값을 얻게끔 하여 영상 해석을 용이하게 합니다.

하지만 CNN의 단점으로는 컨볼루션 연산을 하는 작업이 영상 전체에 대해서 하기에는 꽤 많은 시간이 걸린다는 점입니다. 그래서 영상에 MaxPooling을 적용시킴으로써 연산 시간도 줄이고, 영상의 translation과 position invariance를 가지게끔 하였습니다. 하지만 이러한 풀링은 해당 지역의 가장 큰 특징값만을 가져오는 것이기 때문에, 영상 속 물체의 큰 특징들은 가져오지만, 그 외의 다양한 정보 및 위치 관계를 잃어버리기 때문에 큰 문제가 발생합니다.

예를 들어 위의 사진 속 얼굴을 보시면, 오른쪽 얼굴에 경우 눈,코,입의 위치적 관계가 전혀 엉망이지만, MaxPooling을 통한 CNN은 다음과 같은 사진도, 중요한 핵심인 눈,코,입이 존재하기에 정상적인 얼굴로 인식하는 것입니다.
그래서 해당 논문에서는 각 특징들이 있는지 없는지를 판단하는게 아닌, 보다 정밀한 특징(위치 관계)를 파악하는, 보다 고차원 공간을 바라보는 네트워크인 캡스넷(CapsNet)을 제안합니다.

Capsule

캡스넷은 Capsule network의 준말로, 이 논문에서는 캡슐(Capsule)이라는 용어가 자주 나오는데, 여기서 캡슐이란 뉴런이 하나가 아닌 여러개가 존재하는 작은 그룹을 말합니다. 기존 CNN에서 영상을 표현하는 하나의 픽셀을 뉴런이라고 지칭한다면, 해당 논문에서는 이 뉴런을 여러개 모아서 캡슐이라고 부릅니다.

기존의 뉴런 하나로는 하나의 엔티티를 특성들을 모두 표현할 수 없다면 활성화된 캡슐을 가진 뉴런은 영상안에 특정 엔티티(entity)에 대한 다양한 특성을 표현할 수가 있습니다. 여기서 말하는 다양한 특성의 예시로는, pose( 위치, 크기, 방향), deformation, velocity, texture 등등을 말합니다. 즉 캡슐 속에 존재하는 각각의 뉴런들이 각자 특성을 하나씩 표현하고 있겠죠?

여기서 가장 중요한 점은 영상 속에 이러한 entity를 어떻게 찾느냐는 것입니다. 해당 논문에서는 인스턴스 파라미터(위에서 예시를 든 pose, velocity 등과 같은 엔티티의 특성들)의 벡터 길이(length)를 통하여 엔티티의 존재 여부를 알아낼 것이며, 또한 엔티티의 특징들을 더 잘 표현할 수 있게끔 벡터의 방향성을 더 강조한다고 합니다. 이 때 캡슐의 출력 벡터의 길이는 비선형 함수를 적용시켜서, 방향은 바꾸지 않고, 크기만 줄여나감으로써 벡터 길이가 1이 넘지 않도록 합니다. 벡터의 길이를 1이 넘지 않게끔 한 이유는, 이를 통해 우리가 찾기 원하는 entity가 해당 위치에 존재하는지를 확률적으로 나타내기 위함입니다.

How the vector inputs and outputs of a capsule are computed?

그렇다면 이러한 캡슐 벡터는 어떻게 구할 수 있을까요? 먼저 캡슐 벡터의 크기(길이)는 현재의 입력값에 의해 결정됩니다. 여기서 위에 언급한 비선형 함수 “squashing”이라는 개념이 나오는데, 이 함수를 통해 작은 값을 지니는 벡터는 0에 가깝게, 또 큰 값을 지니는 벡터는 더 큰 값(1)에 가깝게 만들어 줍니다.
squashing 함수의 식은 다음과 같습니다.

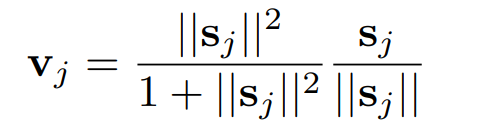
그림1 캡슐 벡터의 크기를 0~1로 만들어주는 비선형 함수

• v_{j} : 캡슐 j의 출력 벡터
• s_{j} : 캡슐의 전체 입력

전체 입력에 해당하는 s_{j} 는 다음과 같습니다.

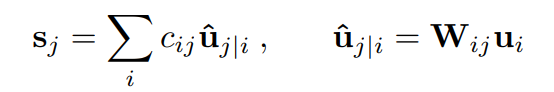
그림2

• c_{ij} : coupling coefficient
• \hat{u} _{j|i} : 전체 예측 벡터
• W_{ij} : 가중치 행렬

캡슐의 첫번째 레이어를 제외한 모든 레이어에 대하여, 캡슐의 전체 입력 s_{j} 는 예측된 벡터 \hat{u}_{j|i} 전체에 대하여 가중치를 곱한 것입니다. 그리고 이 때 \hat{u}_{j|i} 는 단순히 가중치 행렬에 캡슐 u_{ij} 를 곱한 것 입니다.

coupling coefficient는 다음과 같이 구할 수 있습니다.

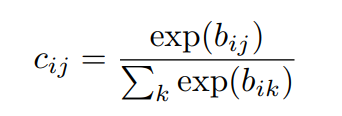
그림3

그럼 이제 이 b_{ik} 는 캡슐 j의 현재 출력 벡터 v_{j} 와 캡슐 i로 만들어진 전체 예측 벡터 \hat{u} _{j|i} 의 agreement를 계산한 후( \hat{u} _{j|i} ·v_{j} ) 이를 업데이트하여 구할 수 있습니다.

계속해서 수식만을 나열했기에 많이 이해가 힘드실 수 있다고 생각이 들어 해당 수식을 정리해 보겠습니다.

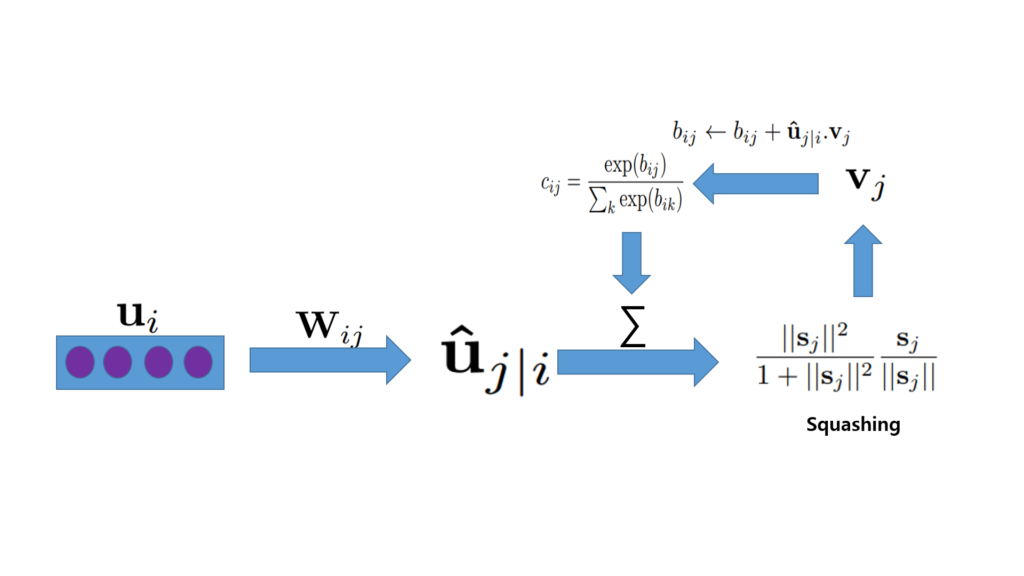
1. u_{i}W_{ij} = \hat{u}_{j|i}
2. ∑\hat{u}_{j|i} c_{ij} = v_{j}
3. b_{ij} = b_{ij} + \hat{u}_{j|i} +v_{j}
   이런 방향으로 계산을 하고 있으며 이것이 바로 Routing algorithm입니다.

Routing algorithm

CapsNet architercture

저의 미숙함으로 위에 수식들을 복잡하게 적어놔서 매우 어렵게 느껴지실 수도 있으시겠지만, 사실 캡스넷의 구조는 및 구현은 매우 간단합니다. 기존 CNN 구조에서 feature map의 채널의 크기를 캡슐 속 뉴런 갯수만큼 나누어서 생각해주면 됩니다.

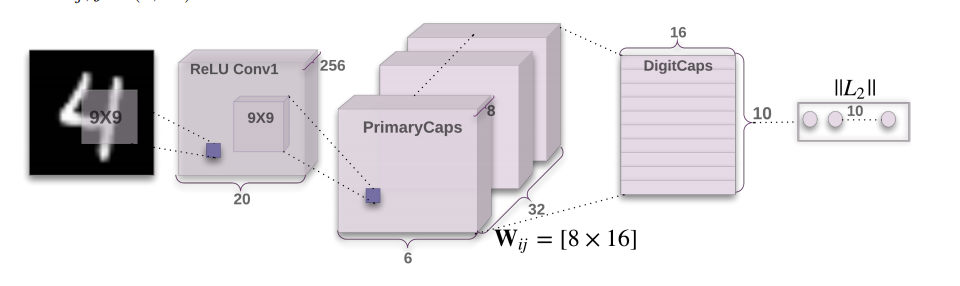
입력 영상으로 MNIST를 넣었을 때, 기존 CNN처럼 9×9 크기의 필터 256개를 적용시켜 20×20×256 feature map을 만듭니다.(참고로 MNIST는 28×28의 영상크기를 가집니다.)

그리고 2번째 레이어(PrimaryCaps)에서 feature map을 캡슐화시키는데, 해당 논문에서는 하나의 캡슐 안에 8개의 뉴런이 들어가기 때문에(8D capsule) , 첫번째 레이어에서 256개의 채널을 8로 나눈 32채널이 두번째 레이어의 채널값이 됩니다. 또한 두번째 레이어는 9×9 필터에, 스트라이드 값을 2로 놓고 연산하여서 feature map의 크기는 6×6이 됩니다.

마지막 레이어(DigitCaps)는 하나의 digit당 16D 캡슐을 가지고 각각의 캡슐들은 레이어에 존재하는 모든 캡슐로부터 입력값을 받습니다.

뒤에 loss와 결과에 대한 내용이 남아있지만 생각보다 내용 이해 및 정리가 힘들기도 하고 시험기간이기도 하여서 현재는 여기서 마무리 짓고 추후 내용을 추가하도록 하겠습니다.