
두 영상에서 동일한 지점을 찾아내는 알고리즘으로는 대표적으로 SIFT, SURF 등등 이 있습니다. 그러나 두 영상이 실내에서 촬영되어 그렇다할 특징들이 없다면 두 영상을 매칭하는데 있어 큰 어려움이 존재하게 됩니다. 오늘 리뷰할 논문은 이러한 실내 상황에서 선을 이용하여 매칭의 성능을 올린 논문입니다.
1. Line Matching by Point Correspondences
우선적으로 용어들은 다음과 같습니다.
- reference 영상들로부터 얻어낸 line segment
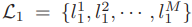
- query 영상들로부터 얻어낸 line segment
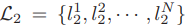
- SIFT 같은 알고리즘으로 얻어내어 잘못 매칭되었다고 예상되어지는 잠재적인 point correspondence
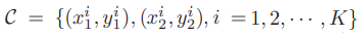
- 최종적으로 알아내야할 matching line set
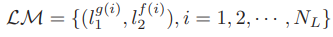
query와 referece 사이의 correspondence들로 두 영상간의 정확하지는 않은 rotation 관계를 알아내고 이를 이용하여 L1과 L2 사이의 빠르고 강인한 매칭하는 것이 주 목표입니다.
1.1 The Affine Invariant
한 쌍의 영상에서의 line set이 각각 l, l’ 이고 두 선이 affine transform H 사이 관계에 놓여있고 한 쌍의 점 (X1, X1′)과 (X2, X2′)도 마찬가지로 H 사이의 관계에 놓여있다면 다음과 같은 식을 얻을 수 있습니다.
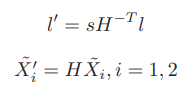
물결 표시가 붙어있는 것은 점과 homogeneous 하다는 의미입니다. 그리고 두 점사이의 관계를 (6)과 같이 정의할 수 있습니다.
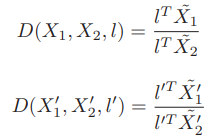
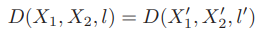
(5)의 식과 (6)의 식을 이용하면 (7)과 같은 결과를 얻을 수 있습니다. (7)을 통해 D(X1, X2, l)은 affine invariant 한 것을 증명할 수 있으며 한 쌍의 점을 line matching에 이용할 수 있다는 것도 알 수 있습니다.
1.2 The Similarity of Two Lines
1.1에서 설명드렸던 것처럼 invariant하게 두 선을 매칭시키려면 우선적으로 C에서 이 선들과 같은 평면 위에 있다고 여겨지는 점들을 이용하게 됩니다. 이 점들은 선 주변에 있기에 affine transform H를 근사한다고 여겨질 수 있습니다. 왜냐면 주로 영상에서의 선들은 실제로 나뉜 선이라기보단 주로 표면상 에지이기에 선으로 나뉜 양 쪽 중에 한 쪽은 적어도 동일 평면일 수 있다고 말할 수 있습니다. 같은 평면인 한 쪽은 선에 존재하는 모든 점의 기울기로 구해질 수 있으며 동일 평면인 영역이 정해지면 이 영역에 해당하는 점을 C에서 찾아오게 됩니다. C에서 선 l과 이웃한 점 P를 찾아오려면 선 l과 점 P 사이의 거리가 alpha*length(l) 보다 작아야하며, 선 l의 수직이등분선과 점 P 사이의 거리가 beta*length(l) 보다 작아야합니다.
이러한 조건으로 점 P의 집합을 구하더라도 에러는 존재하게 됩니다. 그러나 점 P의 집합을 모두 이용하는 것이 아닌 일부만 있으면 되기 때문에 이를 감안한다고 하며 저자는 선의 오검출을 줄이기 위해서 길이가 20 pixel 미만인 선은 배제했다고 합니다. 또한 alpha 는 2.0, beta 는 0.5로 두었습니다.
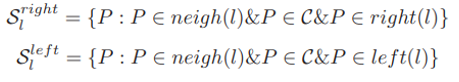
위에서 설명한 조건으로 같은 선의 이웃하는 점들을 찾아낼 수 있으며 (8)에서처럼 만약 선의 오른쪽에 존재할 시 S_{l}^{right}, 선의 왼쪽에 존재할 시 S_{l}^{left} 로 나타낼 수 있게 됩니다. 이렇게 한 쌍의 선 양 쪽에서 이웃 점들을 찾아낸 뒤 왼쪽과 오른쪽 각각 모든 점과의 유사도를 구하고 이 중 최대값을 두 선의 왼쪽과 오른쪽의 유사도로 채택하게 됩니다.
1.3 Fast Matching
이미지 상의 모든 점들은 각각 다른 orientation을 갖게 됩니다. 이를 이용해 저자는 좀 더 빠른 matching 을 진행하였습니다. 우선 위에서 이웃점을 뽑았던 C 집합은 SIFT와 같은 알고리즘으로 얻어냈었습니다. SIFT로 keypoint를 뽑게되면 각 점마다의 orientation도 구해지게 되는데, 모든 점의 orientation을 모아 histogram을 쌓은 후 가장 큰 orientation 값을 근사된 global orientation theta 로 사용하게 됩니다. 이렇게 얻은 theta 를 이용하여 1.2에서 설명드렸던 왼쪽과 오른쪽의 모든 점에서 유사도를 구할 때 (9)와 같은 조건으로 t_{theta} 는 20으로 두고 필터링하여 빠르고 강인하게 매칭을 하였다고 합니다.
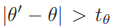
2. Result






앞서 설명드린 선과 그 이웃을 이용하여 유사도를 구하고 매칭을 했을 때 각 환경에 따른 결과입니다. 각각 scale이 변했을 때, scale과 rotation이 변했을 때, rotation이 변했을 때, 밝기가 변했을 때, occlusion이 있을 때, viewpoint가 변했을 때의 결과이며 정확한 매칭이 이루어졌다는 것을 확인할 수 있습니다.
3. Reference
[1] http://vision.ia.ac.cn/Students/bfan/BinFan_LM_CVPR10.pdf
1. Edge를 통해 특징을 추출하는 방법은 Hough Transform 등이 있을텐데 다른 연구와 비교했을 때 개선된 사항에 대해 알고 싶습니다. 또한, 이 논문은 구별점이 뚜렷하지 않은 실내에서 잘 구별하기 위한 것으로 동기를 말했는데 정작 예시 그림들은 실외 그림들이네요. 이미지에서 동일한 패턴이 많은 가운데 특징을 나타내는 edge를 잘 찾아내는 것은 결과로 알겠습니다만 실제 SIFT, SURF와 비교한 결과는 없는 건가요?
2. 죄송하지만 방법론에 대해서 이해하기 힘들었습니다. 각 영상에서 특징을 표현하는 line들을 찾고, scale의 경우는 길이 차이일뿐 다르지 않다는 점에서 scale invariant 한 것 같고, 문제는 rotation을 어떻게 알아내냐는 것일텐데 식7에서 affine invariant 하다는 점을 이해하지 못해 막힌 것 같습니다.
1. 다른 Line matching 방식인 LS(Line signature) 와 Result의 이미지 쌍들에 대해 매칭 성능 비교를 했을 때 occlusion 쌍을 제외하고 1~4% 정도의 성능향상을 보였으며 또 다른 방식인 MSLD 와 비교했을 때는 모든 쌍에서 1~50% 가량의 성능향상을 보였습니다. 그리고 사실 논문이 주로 소개한 동기는 outlier을 포함한 SIFT keypoint 를 이용해서 line 을 빠르고 강인하게 매칭하는 것인데 제가 이 논문을 실내 localization 챌린지에 적용하려고 읽은 생각에 bias 되다보니 동기를 소개하는 부분에 있어 실수를 한 것 같습니다..ㅎ 그리고 본 논문에서는 SIFT의 keypoint를 이용하여 line matching을 하는 것이 목표이기에 다른 keypoint를 추출하는 알고리즘과 비교한 결과는 따로 소개되어있지 않습니다.
2. 리뷰의 식 (5) 를 통해 얻어낸 식 (6), (7) 은 각 점과 선사이의 거리의 비율을 의미하며 H 변환 되기 이전 homogeneous coordinate의 두 점들의 이 비율과 H 변환 후의 이 비율이 같아서 affine invariant 하다고 합니다.
전체적으로 작성 시의 몸상태가 많이 안좋았어서 글의 설명이 친절하지 않은 경향이 있습니다. 이부분에 대해 사과드리며 추후 더 쉽게 이해할 수 있도록 내용을 추가할 계획이 있습니다! (…언젠가..?)