Mingxing Tan, Quoc V. Le
이번 리뷰에는 2020 PD 에서 제가 backbone으로 사용했던 efficientNet에 관련해서 정리해보도록 하겠습니다.
제가 이해한 이 논문의 핵심에 대해서 요약하면 다음과 같습니다.
“Compound model scaling을 통한 효율적인 파라미터 수를 가지고 성능 향상“
이 논문에서는 모델(F)를 고정하고 depth(d), width(w), resolution(r) 3가지를 조절하는 방법을 제안하고 있는데, 이때 고정하는 모델(F)를 좋은 모델로 선정하는 것이 굉장히 중요합니다. 아무리 scaling factor를 조절해도, 초기 모델 자체의 성능이 낮다면 임계 성능도 낮기 때문입니다. 이 논문에서는 MnasNet과 거의 동일한 search space 하에서 AutoML을 통해 모델을 탐색하였고, 이 과정을 통해 찾은 작은 모델을 EfficientNet-B0 이라 부르고 있습니다.
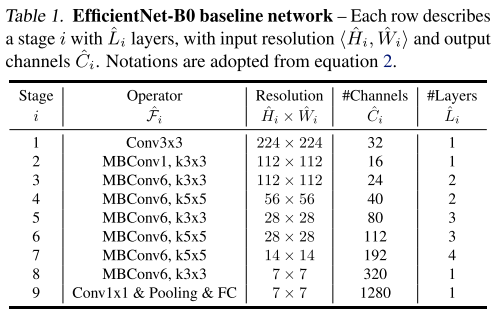
모델 구조는 MnasNet과 거의 유사하며 위의 표와 같은 구조로 구성이 되어있습니다. 이제 이 모델을 기점으로 3가지 scaling factor를 동시에 고려하는 Compund Scaling 을 적용하여 실험을 수행합니다.
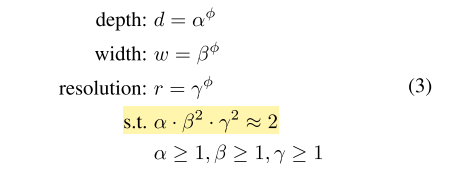
우선 depth, width, resolution 은 각각 알파, 베타, 감마로 나타내며 각각의 비율은 노란색으로 강조한 조건을 만족시켜야 합니다. 이 때 width와 resolution에 제곱이 들어간 이유는 depth는 2배 키워주면 FLOPS도 비례해서 2배 증가하지만, width와 resolution은 가로와 세로가 각각 곱해지기 때문에 제곱 배 증가합니다.
depth 증가는 layer가 증가하는 것이지만 width,resolution 증가는 이미지 사이즈가 증가하므로 (2*2)->(4*4) 는 제곱배가 됩니다.
+FLOPS(초당 부동소수점 연산 수)는 모델의 파라미터 수 정도로 이해하고 있습니다
그래서 제곱을 곱해서 계산을 하고 있습니다. 그 뒤 전체 모델의 사이즈는 알파, 베타, 감마에 똑같은 파이만큼 제곱하여 조절을 하게 됩니다. EfficientNet의 알파, 베타, 감마 값은 간단한 grid search를 통해 구하는 방식을 제안하고 있으며, 처음 단계에서는 파이를 1로 고정한 뒤, 타겟 데이터셋에서 좋은 성능을 보이는 알파, 베타, 감마 값을 찾아냅니다. 본 논문에서는 알파 값은 1.2, 베타 값은 1.1, 감마 값은 1.15를 사용하였으며, 방금 구한 3개의 scaling factor는 고정한 뒤 파이를 키워주며 모델의 사이즈를 키워주고 있습니다.
본 논문에서는 실제로 3가지 scaling 기법에 대해 각 scaling 기법마다 나머지는 고정해두고 1개의 scaling factor만 키워가며 정확도의 변화를 측정하였습니다.
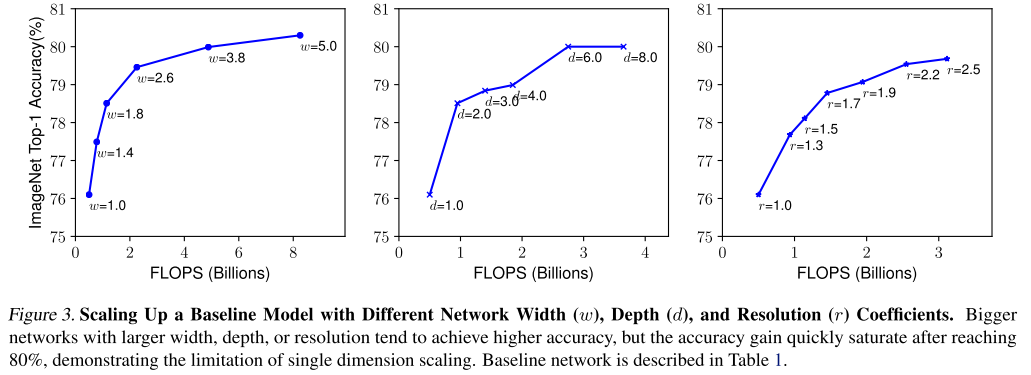
위의 그림을 보시면 width scaling, depth scaling 은 비교적 이른 시점에 정확도가 saturation 되며 그나마 resolution scaling이 키우면 키울수록 정확도가 잘 오르는 것을 확인할 수 있습니다.
위의 실험들을 통해 3가지 scaling factor를 동시에 고려하는 것이 좋다는 것을 간단하게 입증을 하였고 최적의 비율을 찾아서 실제 모델에 적용을 해서 다른 모델들과 성능을 비교하는 과정을 보였습니다.
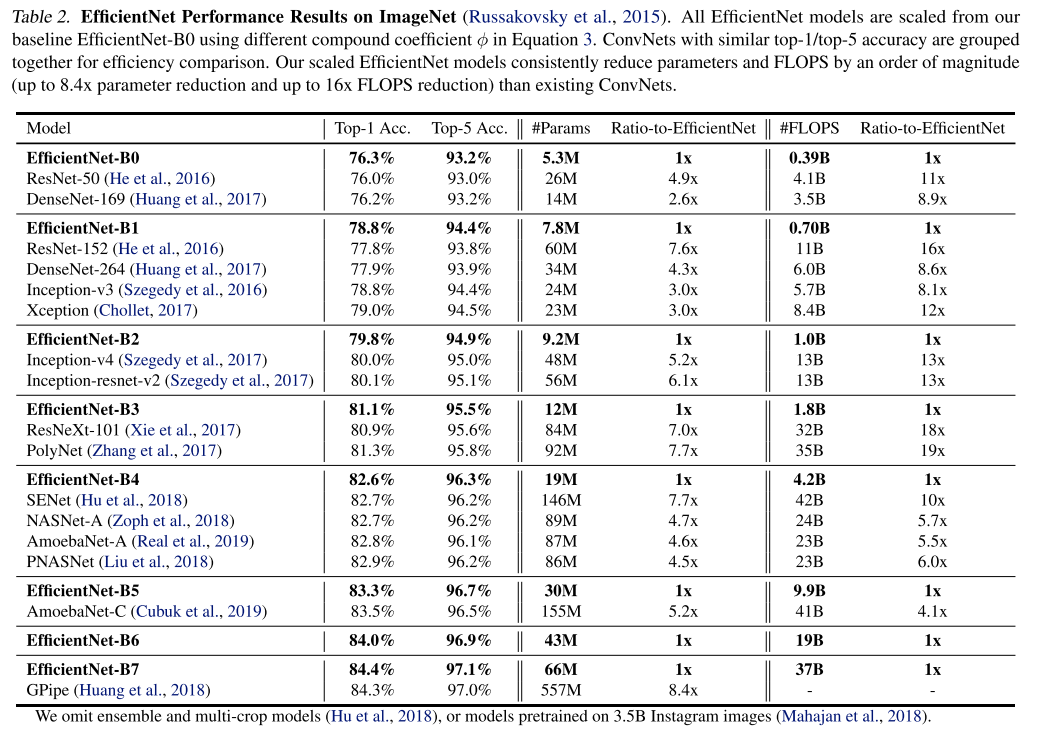
논문에서 핵심적인 부분들을 캐치하여 깔끔한 설명 감사드립니다. 리뷰를 토대로 이해한 바로는 자원적 효율을 위해, 즉 FLOP을 제한하기위해 수식 3의 조건 아래에서 depth, layer, wise를 greed search로 model design을 하였다라고 이해를 했습니다. 여기서 궁금한 점이 모든 모델이 위의 방식을 이용하면 성능 향상을 얻을 수 있다면 논문에서 리포팅을 했을텐데, 리포팅 결과가 있나요? 그리고 모든 모델에 적용이 어렵다면 그러한 이유에 대해 논문에서 이야기 했는지 궁금합니다