해당 논문은 CVPR 2019 workshop – Google Landmark Challenge 상위 수상작들 대부분이 사용한 방법을 제시한 논문입니다. 특히 trainable Pooling인 GeM(Generalize-mean Pooling)을 제안한 논문으로 한번쯤 정리하면 좋을 듯 하여 리뷰를 작성하게 되었습니다. (CVPR 2018 workshop – Google Landmark Challenge에서는 DIR(Deep Image Retrieval: Learning global representation s for image search)가 많이 사용되었습니다.) – git hub
Contributions
- Hard non-matching (Neg), Hard matching (Pos)
- Propose novel whitening
- Propose a trainable Pooling (GeM)
- Propose \alpha -weighted QE
- Oxford Building, Paris and Holidays dataset에서 SOTA(Visual retrieval) 달성
Abstract
Image retrieval task에서 CNN는 discriminative power, 표현의 압축성, 검색의 효율성으로 인해 지배적인 입지를 얻었습니다. CNN을 학습시키기 위해서는 처음부터 학습하거나 fine-tuning을 사용하며, 많은 양의 정제된 데이터가 필요합니다. 데이터 셋의 질에 따라 영향을 많이 받기도 합니다. 해당 논문에서는 잘 정제되지 않은 이미지로부터 image retrieval을 하기 위한 완전 자동화된 fine-tune CNNs을 제안했습니다. SOTA를 달성한 3D model(SfM, retrieval)의 영상들로부터 train data를 선택하여 학습합니다. 3D model에서 얻은 기하학과 카메라 위치를 이용한 hard-negative, hard-positive로 성능을 향상 시켰으며, 차별적으로 학습한 CNN descriptor의 whitening은 일반적으로 사용되는 PCA의 whitening보다 뛰어나다는 것을 보여줍니다. 또한 Max, Average Pooling을 일반화하고 retrieval 성능을 향상시키는 훈련 가능한 GeM(Generalized-Mean) Pooling을 제안합니다. 제안한 방법은 VGG 네트워크를 적용하여 Oxford building, Paris, Holiday dataset에서 SOTA를 달성했습니다.
Fully convolution network
해당 방법론은 VGG, AlexNet, ResNet과 같은 일반 객체 인식에서 인기 있는 CNN을 채택했으며, fc layer는 사용하지 않는다. 해당 모델을 사용하는 것은 fine-tuning을 수행하기 위해 좋은 초기화를 제공합니다.
입력 영상이 주어졌을 때, 출력은 3D tensor( \mathcal{X} of W \times H \times K )가 나옵니다. ( \mathcal{X}_k, \in \{1 ... K\} 는 W \times H 인 2D feature map에 해당합니다. ) 추가적으로 마지막 층을 ReLU를 이용하여 음이 값이 없는 것으로 가정합니다.
Generalized-mean pooling and image descriptor
CNN으로 추출된 \mathcal{X} 을 Pooling layer에 태워 vector \mathbf{f}을 추출합니다.
기존 Global Max Pooling(MAC vector)는 다음과 같은 식으로 구성됩니다.
\mathbf{f}^{(m)} = [latex] [ f_{1}^{(m)} . . . f_{k}^{(m)} . . . f_{K}^{(m)} ], f_{k}^{(m)} = \underset{x \in \mathcal{X}}{\max{x}} (1)
Average Pooling(SPoC vector)일 경우,
\mathbf{f}^{(a)} = [latex] [ f_{1}^{(a)} . . . f_{k}^{(a)} . . . f_{K}^{(a)} ], f_{k}^{(a)} = f_{k}^{(a)} = \frac{1}{ \left| \mathcal{X}_{k} \right| }\sum_{x \in \mathcal{X}_{k}} x (2)
해당 논문은 Max, Average를 일반화하여 표현할 수 있도록 멱평균 (Generalized-mean)을 이용한 Pooling을 제안합니다.
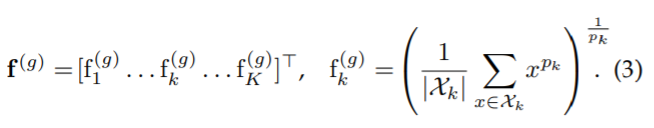
멱평균으로 표현함으로써 (1)과 (2)는 (3) GeM Pooling으로 표현할 수 있습니다. p_k → ∞ 일 때, Max pooling 해당하며, p_k = 1 일 경우, Average pooling에 해당합니다. 최종적으로 feature vector는 feature map당 하나의 값을 가지게 됩니다. dimension은 K를 가지게 되며, 인기있는 객체 인식 네트워크에서는 이는 256, 512, 2048 크기의 컴패트한 이미지 표현을 가지게 됩니다.
Pooling parameter p_k 는 미분이 가능하기 때문에 back-propagation의 일부가 될 수 있으므로 수동적으로 설정하거나 학습을 할 수 있습니다. 아래의 식은 (3)의 미분식입니다.
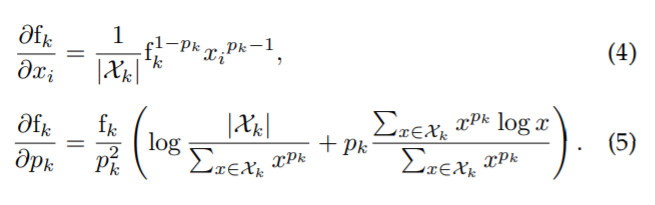

Max pooling(MAC, Fig 2. VGG off-the-shelf)의 경우, feature map당 하나의 식으로 도출됩니다. 각각의 기술자의 구성 요소는 이미지의 특징적인 이미지 패치를 가지고 있다고 볼 수 있습니다. 한 쌍의 영상을 기술자의 내적을 통해 유사성을 평가합니다. 각 대응의 강도는 기술자의 구성 요소의 product에 영향을 받습니다.
제안하는 GeM(Fig 2. VGG ours)의 경우, Fig 2.를 볼 수 있듯이 유사성에 크게 기여하는 이미지 패치를 대응을 보여줍니다. pooling 자체가 fine-tuning 후에 개선하기 때문이다. Fig 2.를 보면 자동차와 자전거와 같은 ImageNet class에 덜 잡는다.
+ 쉽게 이야기하자면, object recognition으로 pre-trained model을 사용하여 fine-tuning을 할 때, pooling도 조정해주지 않으면 얻고자 하는 물체에만 관심을 갖지 않고 pre-train 시 사용한 데이터 셋에 속하는 클래스에도 관심을 가지게 된다고 합니다.

Fig 3. 에서는 GeM Pooling layer와 fine-tuning VGG와 일치하는 query, DB 영상의 예시를 보여줍니다. 해당 그림은 유사성이 큰 non-matching image와 구별하는 데 큰 기여를 한 feature map을 보여줍니다.
마지막 네트워크 계층은 L2로 구성되며, vector f는 L2-norm으로 두 영상 사이의 유사성을 내적으로 평가합니다.

Fig 4.는 GeM의 parameter인 p_{k} 을 고정된 값으로 학습한 feature map을 예시로 보여줍니다. 또한 p_{k} 값이 커질 수 록 feature map에 좀 더 지역적으로 관심을 가지는 것을 볼 수 있습니다.
Siamese learning and loss function
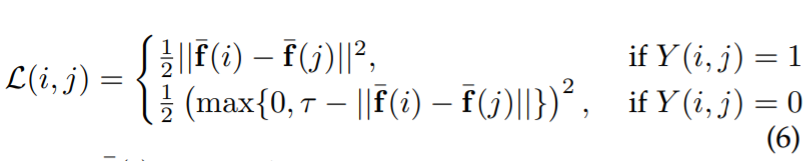
- ( i, j ) : 입력 영상 쌍
- \bar{\mathbf{f}} : L2-norm GeM vector
- Y (i, j) \in { 0, 1 } : match = 1, nor 0
- \tau : margin parameter
Whitening and dimensionality redution
이전 기존의 방법들은 PCA를 이용하여 차원 축소를 했습니다. 해당 파트에서는 fine-tuned GeM vector를 고려한 차원 축소(post-processing)를 제안합니다.
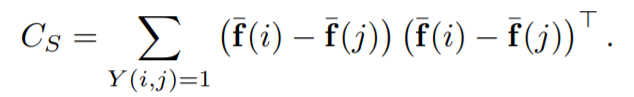
C_S 는 matching pairs에 대한 식이며, whitening part에 해당합니다.
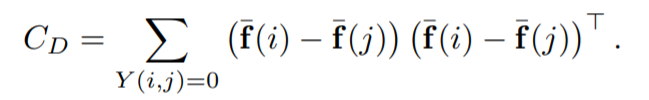
C_D 는 non-matching pairs에 대한 식이며, rotation part에 해당 합니다.
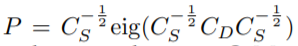
Projection P는 아래의 식에 적용됩니다.
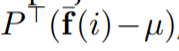
u는 GeM vector의 평균입니다.
적용된 내부의 식만 조금 다르고 큰 틀은 PCA에 해당하기 때문에 구체적인 내용은 생략하겠습니다.
Appendix A: Whitening
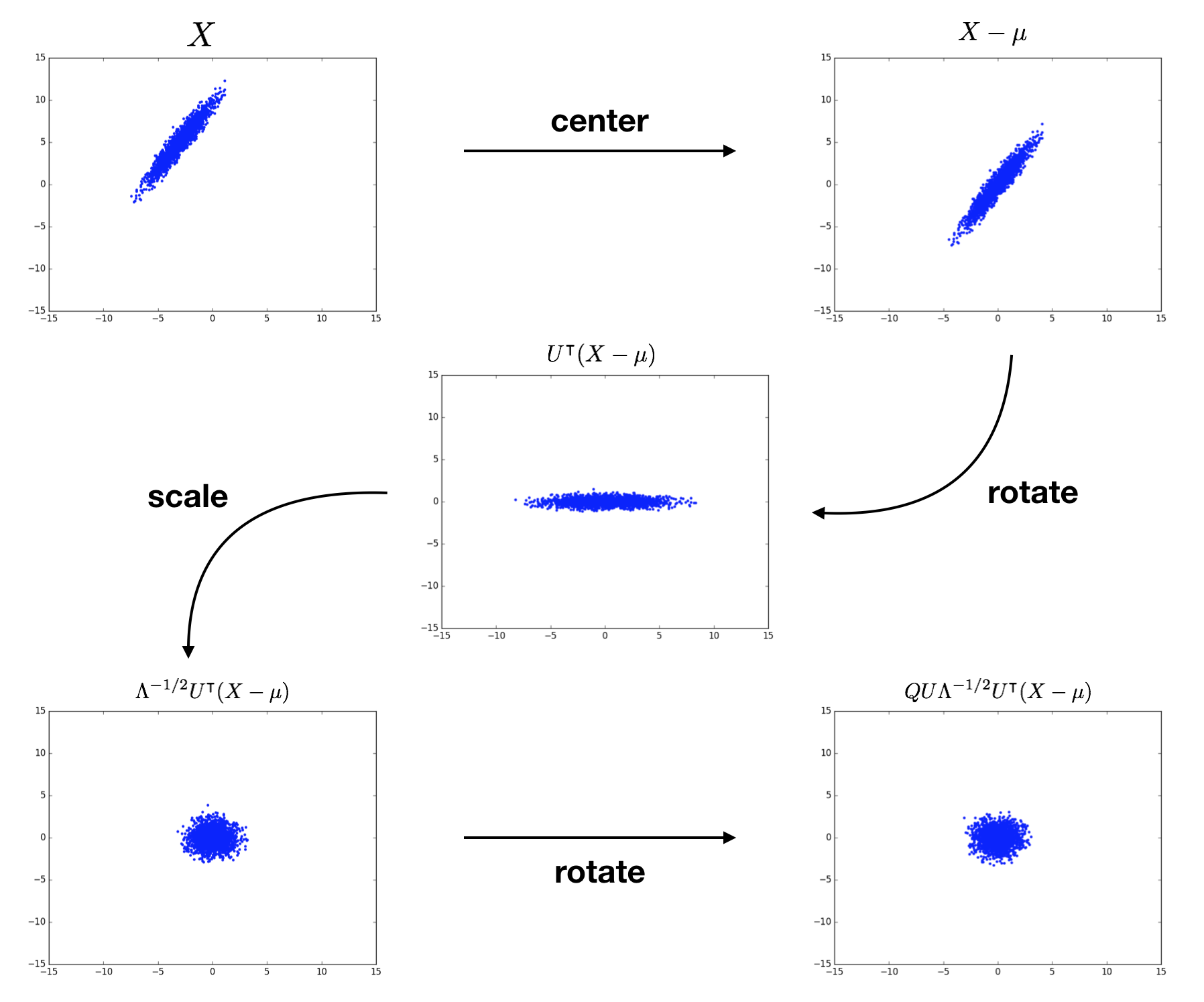
Appendix B: Generalized-mean
Appendix C: PCA