1 Introduction

2 Detection of scale-space extrema
scale space는 우선 가우시안 필터를 통해 스케일(시그마)을 키워가고 다운 샘플링을 하며 만들게 됩니다.이를 블러된 이미지라 하며 아래 수식에서 L(x,y,sigma)로 표현됩니다.이과정을 겪는 이유는 다양한 스케일에서 키포인트를 추출할 수 있도록 스케일 불변성을 얻기위한 과정입니다.
왜 Gaussian filtering and Down sampling을 함께 쓰는지에 대한 의문이 있었습니다. 그 이유는 Gaussian 필터를 통해 시그마를 늘리면 스케일이 커지는 효과가 있고 이미지 사이즈를 다운 샘플링 해도 마찬가지의 효과가 있는데 그럼 하나만 쓰지 왜 두개를 같이 쓸까요?
답변 1.계산의 효율성과 메모리 용량의 효율적 소비를 위해
답변 2.일반적으로 Gaussian 필터를 거치지 않고 다운 샘플링 하게 되면 aliasing effects 가 발생가게 됩니다 따라서 이를 피하기 위함이죠


이후 블러된 이미지 L을 각 스텝사이즈(k*sigma,스케일 공간에서 스텝사이즈는 +-로 진행하지 않고 */로 진행합니다)를 통해 빼주어 D(x,y,sigma)를 얻게 됩니다.이는 각 이미지에서 코나와 엣지 정보들을 두드러지게 해주는 과정입니다.

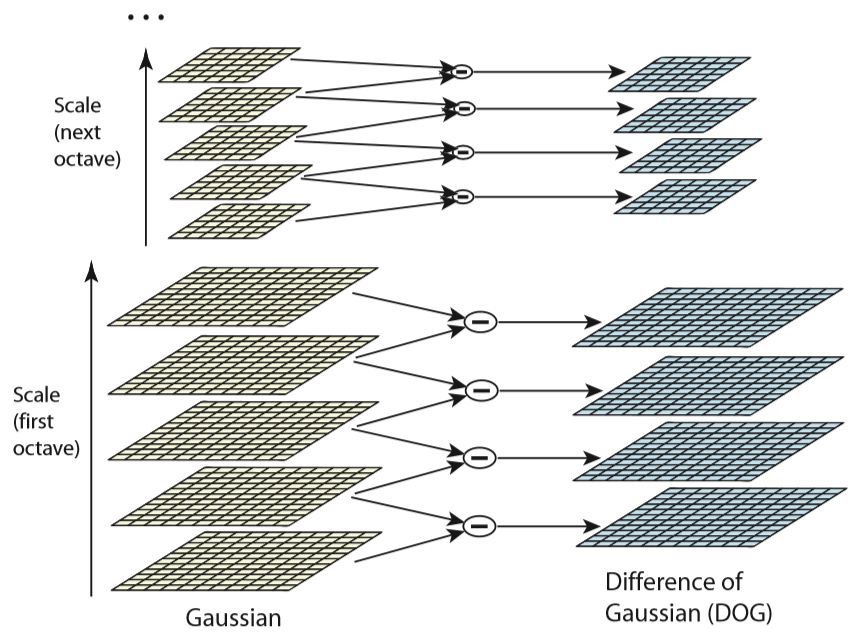
이 과정은 원래 LOG( Laplacian of Gaussian)을 통해 이뤄지지만 계산의 효율성을 위해 근사 처리를 통해 DOG( Difference of Gaussian )를 사용할 수 있습니다.
LoG연산자의 원리는 이미지를 블러한 후 2차미분을 계산합니다.

DoG 연산은 이를 인접한 두 블러이미지를 빼주는 것으로 진행합니다.이에 대한 증명은 아래와 같습니다.

3.keypoint check
먼저 DoG 이미지들 내에서 극대값, 극소값들의 대략적인 위치를 찾습니다.
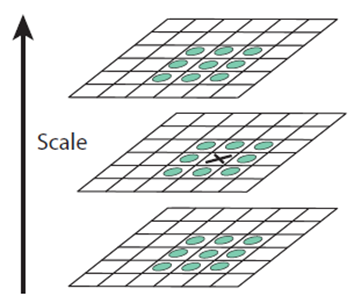
한 픽셀에서의 극대값, 극소값을 결정할 때는 동일한 octave내의 세 장의 DoG 이미지가 필요합니다. 체크할 DoG이미지와 scale이 한 단계씩 크고 작은 DoG 이미지들이 필요합니다.
픽셀과 가까운 9개씩, 총 26개를 검사합니다. 픽셀의 값이 26개의 이웃 픽셀값 중에 가장 작거나 가장 클 때 keypoint로 인정이 됩니다.
그런데 우리는 이 진짜 극소값, 극대값들의 위치에 접근할 수 없습니다. 그래서 subpixel 위치를 수학적으로 찾아내야 합니다(by Taylor expansion)
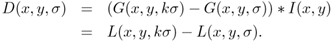
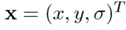
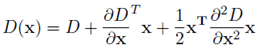
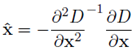
4.Accurate keypoint
이제 전 단계에서 극값들로 찾은 keypoint들 중에서 활용가치가 떨어지는 것들은 제거해줘야 합니다
첫번째는 낮은 콘트라스트를 갖고 있는 것들을 제거해줍니다. keypoint들의 픽셀의 값이 특정 값(threshold)보다 작으면 제거해줍니다.
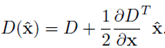

두번째는 엣지 위에 존재하는 것들을 제거해줍니다 .DoG가 엣지를 찾아낼 때 매우 민감하게 찾아내기 때문에, 약간의 노이즈에도 반응할 수 있는 위험이 있습니다. 즉, 노이즈를 엣지로 찾아낼 수도 있다는 것입니다.
우리의 목적은 코너에 위치한 keypoint들만 남기는 것입니다. Hessian Matrix를 활용하면 코너인지 아닌지 판별할 수 있다고 합니다.
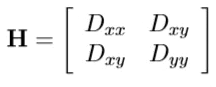


Hessian Matrix의 eigenvalue는 D이미지의 곡률과 정비례하게 되는데요 이를 통해 코너를 수학적으로 정의할 수 있습니다.하지만 eigenvalue의 반복적인 계산은 비효율적이므로 Trace와 Determinant연산자를 통해 위와 같은 부등식을 만족할 때와 동일한 문제로 바꾸어 계산의 효율성을 얻게 됩니다.
5.Orientation assignment
하나의 keypoint 주변에 윈도우를 만들어준 다음 가우시안 블러링을 해줍니다. 이 keypoint의 scale값(블러의 정도를 결정해주는 파라미터)으로 가우시안 블러링을 해줍니다.
그 다음에 그 안에 있는 모든 픽셀들의 그레디언트 방향과 크기를 다음의 공식들을 이용해서 구합니다.
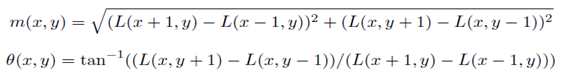
그래서 만약 28도면 3번째 bin을 그레디언트 크기만큼 채우는 것입니다.
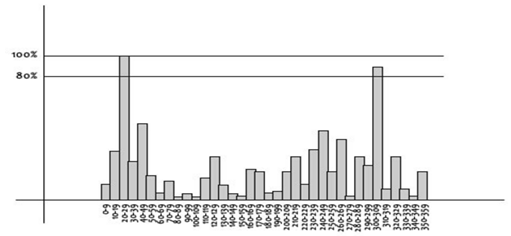
하지만 지배적인 방향이 하나가 아닐 수 있겠죠 그래서 논문은 다음과 같은 multiple peak를 제안합니다.

즉 가장 높은 peak를 100%로 80%이상에 해당하는 peak를 또다른 방향으로 할당하는 것이죠 이는 같은 위치에 같은 스케일에 방향만 여러개인 키포인트를 생성하게 되고 약 전체 키포인트 중 15퍼센트 까지만 multiple orientation을 갖게 됩니다.이는 매칭의 안정성에 굉장히 긍정적인 영향을 미친다고 나와있네요.
6.Descriptor representation
지금까지 keypoint들을 결정해왔습니다. 우리는 지금 keypoint들의 위치와 스케일과 방향을 알고 있습니다. 이제 이 keypoint들을 식별하기 위해 각각의 keypoint의 특징을 128개의 숫자로 표현을 합니다.
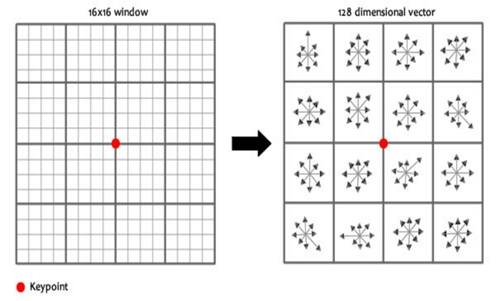
keypoint 주변에 16×16 윈도우를 세팅하는데, 이 윈도우는 작은 16개의 4×4 윈도우로 구성됩니다. 16개의 작은 윈도우에 속한 픽셀들의 그레디언트 크기와 방향을 계산해줍니다. 전 단계에서 했던 것과 비슷하게 히스토그램을 만들어주는데, 이번에는 bin을 8개만 세팅합니다역시 그레디언트 방향와 크기를 이용해서 bin들을 채웁니다.
16개의 작은 윈도우마다 8개의 bin값들이 있으므로, 16 x 8을 해주면 128개의 숫자(feature vector)를 얻게 됩니다.
회전 의존문제를 해결하기 위해 keypoint의 방향을 각각의 그레디언트 방향에서 빼줍니다. 그러면 각각의 그레디언트 방향은 keypoint의 방향에 상대적이게 됩니다. 밝기 의존성을 해결해주기 위해서 정규화를 해줍니다.
Reference
paper:
Distinctive Image Features from Scale-Invariant Keypoints
web: